萤火虫算法综述

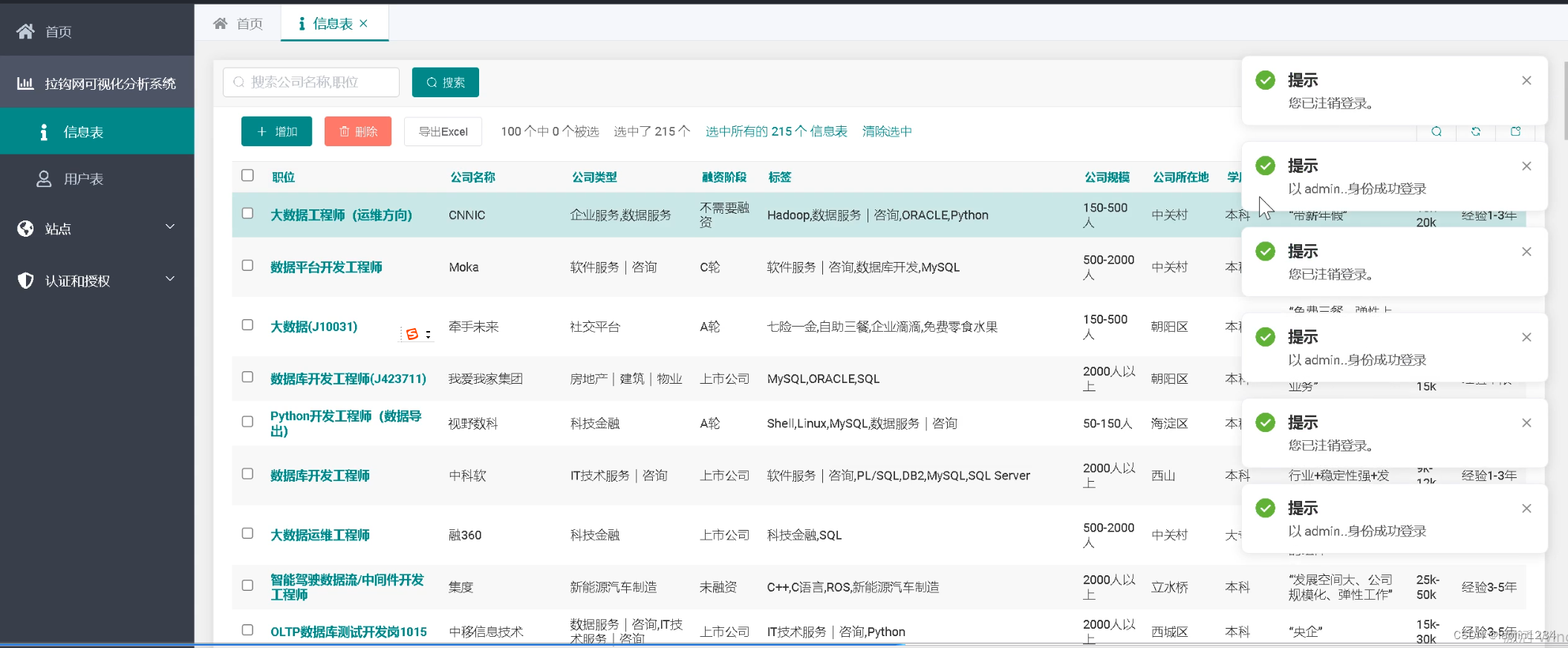
1.萤火虫算法概述

萤火虫闪烁的光芒在热带和温带地区的夏季天空中是一道令人惊叹的风景。大约有两千种萤火虫，大多数萤火虫会发出短暂而有节奏的闪光。闪光的模式对于特定物种来说往往是独一无二的。闪光是由生物发光过程产生的，这种信号系统的真正功能仍在争论中。然而，这种闪光的两个基本功能是吸引交配伙伴（交流）和吸引潜在猎物。此外，闪光还可以作为一种保护性警告机制。

有节奏的闪光、闪光的频率和时间构成了将两性联系在一起的信号系统的一部分。在同一物种中，雌性萤火虫对雄性萤火虫独特的闪光模式做出反应，而在某些物种中，如photuris（萤火虫中的一种肉食动物），雌性萤火虫可以模仿其他物种的交配闪光模式，从而引诱并吃掉可能误认为闪光是潜在合适配偶的雄性萤火虫。

我们知道，距离光源特定距离处的光强度服从平方反比定律。也就是说，光照强度I 随着距离r的增加而减小。此外，空气吸收的光随着距离的增加而变得越来越弱。这两个综合因素使得大多数萤火虫只在有限的距离内可见，通常在夜间几百米，这通常足以让萤火虫交流。

而萤火虫算法是由剑桥大学学者 Xin-She Yang于 2008 年提出的一种新型的自然启发式优化算法，该算法模拟自然界中热带萤火虫的发光机制和行为方式，是一种基于群体智能的随机搜索算法。

为了构建萤火虫算法的数学模型，使用以下三个理想化准则：

（1）算法中的所有萤火虫都不分雌雄，即萤火虫之间的吸引只基于亮度信息，不考虑性别的影响。

（2）萤火虫之间的吸引力和亮度成正比，亮度越大，吸引力越强。且两者都将随着距离的增大而减小。因此对于任意两只萤火虫，亮度小的萤火虫会向亮度大的萤火虫移动，亮度最大的萤火虫将随机移动。

（3）萤火虫的光亮度与待优化目标函数的值有关。

2.萤火虫算法的基本原理

2.1 萤火虫算法的仿生学原理

萤火虫算法的基本仿生学原理：首先，利用搜索空间中的点模拟自然界中的萤火虫个体；其次，将优化过程中的搜索和位置更新过程模拟成自然界中萤火虫个体间相互吸引和移动的过程；将待求解问题的目标函数值模拟成萤火虫个体所处位置处的亮度信息；最后，将迭代过程中寻找最优可行解的过程模拟成萤火虫个体优胜劣汰的过程。

2.2 萤火虫算法的数学模型

由于距离的增加和空气对光的吸收，萤火虫i的亮度会随着距离r的增加而逐渐减小。为了对萤火虫之间的相互吸引力进行建模，本节首先给出萤火虫绝对亮度和相对亮度的定义。

定义 2.1：绝对亮度。对于萤火虫i，初始光强度（r =0处的光强度）为萤火虫i的绝对亮度，记作 $I_{i}$ 。

定义 2.2：相对亮度。萤火虫i在萤火虫j所在位置处的光强度为萤火虫i对萤火虫j的相对亮度，记作 $I_{ij}$ 。

萤火虫算法的核心思想：是萤火虫被种群中所有绝对亮度比它大的萤火虫所吸引，并根据算法中的位置更新公式进行位置更新，不断迭代直至达到算法的停止准则（达到既定的迭代次数或寻优精度。

下面将分别对相对亮度、吸引力和位置更新机制进行数学建模。一般情况下，用待优化函数的目标函数值表示算法的绝对亮度。假设待优化的目标函数是d维的，并假设在解空间内随机初始化的萤火虫的个数为n，则可以用 i=1,2，…，n是一个d维向量，表示该待优化问题的一个潜在解。其中 $x_{i}$ 表示萤火虫i在解空间的位置， $x_{id}$ 表示萤火虫i在第d维空间的值。

萤火虫i的绝对亮度 $I_{i}$ 与 $x_{i}$ 处的目标函数值成正比，即。

绝对亮度的大小可以直接用来衡量萤火虫所代表的潜在解的优劣，即绝对亮度大的萤火虫所代表的潜在解更好，反之亦然。

萤火虫i的亮度随着距离r的增加以及空气的吸收而减弱，定义萤火虫i对萤火虫j的相对亮度为：

其中， $I_{ij}$ 为萤火虫i的绝对亮度。γ为光吸收系数，可设为常数；为萤火虫i到萤火虫j的笛卡儿距离：

假设萤火虫j的绝对亮度比萤火虫i的绝对亮度大，则萤火虫i被萤火虫j吸引而向j移动。这种吸引力的大小是由萤火虫j对萤火虫i的相对亮度决定的，相对亮度越大，吸引力越大。

定义 2.3：吸引力。由萤火虫j 相对亮度的定义，可得萤火虫j对萤火虫i的吸引力为：

其中， $\beta _{0}$ 为最大吸引力，即在光源处（r =0 处）萤火虫的吸引力。

定义 2.4：位置更新。由于被萤火虫j吸引，萤火虫i向其移动而更新自己的位置，i位置更新公式如下：

其中，t为算法的迭代次数； $\varepsilon _{i}$ 是由高斯分布、均匀分布等得到的随机数，为随机项系数。位置更新公式（2-4）由三部分组成。第一部分为萤火虫当前时刻的位置信息，第二项为吸引力项，第三项是带有特定系数的随机项。

2.3 萤火虫算法的算法实现

算法的实现过程可以归纳为：首先将种群中的萤火虫随机散布在待优化问题的解空间内；通过萤火虫所处位置处目标函数公式计算萤火虫所在位置处的绝对亮度，绝对亮度高的萤火虫将吸引绝对亮度低的萤火虫向其移动；根据式（2-3）计算绝对亮度高的萤火虫对绝对亮度低的萤火虫的吸引力强度，并根据式（2-4）对绝对亮度低的萤火虫的位置信息进行更新；最后利用新的位置上的目标函数值更新位置移动后的萤火虫的绝对亮度信息。这样通过有限次的位置的移动，所有的个体都将聚集在绝对亮度最高的萤火虫的位置上，从而实现待优化问题的寻优过程。

定义目标函数
设置算法参数,最大迭代次数MaxGeneration
初始化萤火虫种群
根据处的目标函数值确定各个萤火虫的绝对亮度
While(t < MaxGeneration)for i=1:n 全部萤火虫for j=1:n 全部萤火虫计算和之间的笛卡尔距离if(Ij>Ii)计算萤火虫j对萤火虫i的吸引力根据位置更新公式(2-4)更新萤火虫i的位置end if更新目标函数值及萤火虫亮度end for jfor i重新排列所有萤火虫，找到当前最优解
end while
处理结果并可视化

萤火虫算法需要执行算法初始化和算法迭代两个大的环节。算法迭代过程又包括绝对亮度更新、吸引力更新和位置更新三个阶段。

2.4 萤火虫算法的参数选取策略研究

萤火虫算法的可调节的参数主要包括：光吸收系数γ、最大吸引力 $\beta _{0}$ 和随机项系数 $\alpha$ 。

光吸收系数γ对算法性能的影响

通过对位置移动公式（2-4）的理论分析，根据光吸收系数γ的取值不同，萤火虫算法包含 2 种渐进形式。

当γ→0 时，指数因子→1，此时吸引力项为一常数 $\beta =\beta _{0}$ 。此时，式（2-4）可表示为：

由式（2-5）可以衍生出多个萤火虫算法的变体。首先，当 $\alpha$ =0 时，式（2-5）可以看作改进的差分进化算法（DE）；其次，用当前全局最优解代替时，萤火虫算法将变成加速粒子群算法（APSO）；第三，如果进一步设置=0 ，且的取值与相关，则上式可看作改进的和声搜索算法（HS）。

当γ→∞时，指数因子→0，此时吸引力项，为狄拉克δ函数。光亮度以及吸引力随距离的增加迅速减小，即在萤火虫的可视空间内其他萤火虫的亮度几乎为零。可假设萤火虫在视场模糊的区域内随机游走。此时，式（2-4）可写为:

此时，若 $\alpha$ 以几何冷却方式下降，式（2-6）表示为标准模拟退火算法（SA）[8]；若为一随机数，式（2-6）将变为完全的随机搜索算法。

仿真实验：求四峰函数(2-7)的最优值，由于函数不能通过以往的方法求出其最优值，所以引入群智能优化算法进行求解该函数的最优值，函数如下：

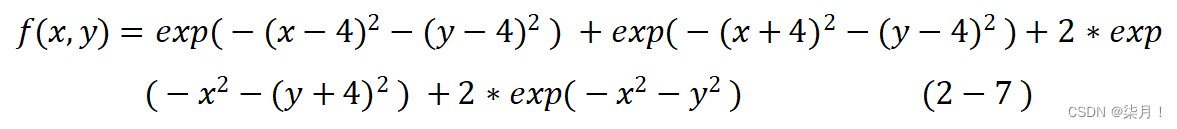
通过matlab仿真实验，当种群规模为15时，根据γ取值的不同，分别计算了当γ=1.0,3.0,5.0,8.0,20.0,100.0时的最优值，并且在代码执行过程中，会自动将子群数分为不同的模块。

代码段：

% ======================================================== % 
% Files of the Matlab programs included in the book:       %
% Xin-She Yang, Nature-Inspired Metaheuristic Algorithms,  %
% Second Edition, Luniver Press, (2010).   www.luniver.com %
% ======================================================== %    % =========================================================% 
% Firefly Algorithm by X S Yang (Cambridge University)     %
% Usage: firefly_simple([number_of_fireflies,MaxGeneration])
%  eg:   firefly_simple([12,50]);                          %
% ======================================================== %
% This is a demo for 2D functions; for higher dimenions,   %
% you should use fa_ndim.m or fa_mincon.m                  %
% Parameters choice: 
% Gamma should be linked with scales. Otherwise, the FA    %
% the efficiency will be significantly reduced because     %
% the beta term may be too small.                          %
% Similarly, alpha should also be linked with scales,      %
% the steps should not too large or too small, often       %
% steps are about 1/10 to 1/100 of the domain size.        %
% In addition, alpha should be reduced gradually           %
% using alpha=alpha_0 delta^t during eteration t.          %
% Typically, delta=0.9 to 0.99 will be a good choice.      %
% ======================================================== %function [best]=firefly_simple(instr)
% n=number of fireflies
% MaxGeneration=number of pseudo time steps
if nargin<1,   instr=[12 50];     end
n=instr(1);  MaxGeneration=instr(2);
% Show info（显示信息）
help firefly_simple.m    %help 得到相关函数的使用格式，并且有助于我们了解该函数的适用场合和使用方法。
rand('state',0);  % Reset the random generator（重置随机发生器）
% ------ Four peak functions（四峰函数） ---------------------
str1='exp(-(x-4)^2-(y-4)^2)+exp(-(x+4)^2-(y-4)^2)';
str2='+2*exp(-x^2-(y+4)^2)+2*exp(-x^2-y^2)';
funstr=strcat(str1,str2);  %strcat(str1,str2) 连接字符串str1和str2
% Converting to an inline function（转换为内联函数：从形式上把你写的表达式变成向量化形式的，返回的是字符串）
f=vectorize(inline(funstr));  
% range=[xmin xmax ymin ymax];
range=[-5 5 -5 5];% ------------------------------------------------
alpha=0.2;      % Randomness 0--1 (highly random)（随机项系数）
gamma=5.0;      % Absorption coefficient（光吸收系数）
delta=0.97;      % Randomness reduction (similar to % an annealing schedule)（最大吸引力）
% ------------------------------------------------
% Grid values are used for display only（网格值仅用于显示）
Ngrid=100;   %画图的时候添加网格线
dx=(range(2)-range(1))/Ngrid;
dy=(range(4)-range(3))/Ngrid;
[x,y]=meshgrid(range(1):dx:range(2),...range(3):dy:range(4)); %meshgrid是MATLAB(一款应用软件)中用于生成网格采样点的函数
z=f(x,y);
% Display the shape of the objective function（显示目标函数的形状）
figure(1);    surfc(x,y,z);  %surf 和 surfc 是通过矩形区域来观测数学函数的函数。surf和surfc能够产生由X、Y、Z指定的有色参数化曲面，即三维有色图。 % ------------------------------------------------
% generating the initial locations of n fireflies（生成 n 只萤火虫的初始位置）
[xn,yn,Lightn]=init_ffa(n,range);
% Display the paths of fireflies in a figure with（在图中显示萤火虫的路径）
% contours of the function to be optimized（待优化函数的轮廓）figure(2);
% Iterations or pseudo time marching（迭代或伪时间行进）
for i=1:MaxGeneration,     %%%%% start iterations
% Show the contours of the function（显示函数的轮廓）contour(x,y,z,15); hold on;   %countour等高线绘图，contour(x,y,z,15)显示了矩阵Z的等值线。绘制由X和Y指定的x-y坐标轴。当X和Y为矩阵时，应该与Z有同样的维数，并且是单调递增的，15为n，表示画15条等高线
% Evaluate new solutions（评估新的解决方案）
zn=f(xn,yn);% Ranking the fireflies by their light intensity（按光照强度对萤火虫进行排名）
[Lightn,Index]=sort(zn);
xn=xn(Index); yn=yn(Index);
xo=xn;   yo=yn;    Lighto=Lightn;
% Trace the paths of all roaming  fireflies（追踪所有漫游萤火虫的路径）
plot(xn,yn,'.','markersize',10,'markerfacecolor','g'); %plot()是matlab中的描点做图函数，一般需要指定横坐标和纵坐标。
% Move all fireflies to the better locations（将所有萤火虫移动到更好的位置）
[xn,yn]=ffa_move(xn,yn,Lightn,xo,yo,Lighto,alpha,gamma,range);
drawnow; %drawnow更新图窗并处理任何挂起的回调。如果修改图形对象并且需要在屏幕上立即查看这次更新，请使用该命令。
% Use "hold on" to show the paths of fireflies（使用“hold on”来显示萤火虫的路径）hold off;% Reduce randomness as iterations proceed（随着迭代的进行减少随机性）
alpha=newalpha(alpha,delta);end   %%%%% end of iterations（结束迭代）
best(:,1)=xo'; best(:,2)=yo'; best(:,3)=Lighto';% ----- All subfunctions are listed here（此处列出了所有子功能） ---------
% The initial locations of n fireflies（n个萤火虫的初始位置）
function [xn,yn,Lightn]=init_ffa(n,range)
xrange=range(2)-range(1);
yrange=range(4)-range(3);
xn=rand(1,n)*xrange+range(1);
yn=rand(1,n)*yrange+range(3);
Lightn=zeros(size(yn));% Move all fireflies toward brighter ones（移动所有萤火虫向更亮的萤火虫）
function [xn,yn]=ffa_move(xn,yn,Lightn,xo,yo,...Lighto,alpha,gamma,range)
ni=size(yn,2); nj=size(yo,2);
for i=1:ni,
% The attractiveness parameter beta=exp(-gamma*r)（计算吸引力参数）for j=1:nj,
r=sqrt((xn(i)-xo(j))^2+(yn(i)-yo(j))^2);
if Lightn(i)<Lighto(j), % Brighter and more attractive（更亮的萤火虫）
beta0=1;     beta=beta0*exp(-gamma*r.^2);
xn(i)=xn(i).*(1-beta)+xo(j).*beta+alpha.*(rand-0.5);
yn(i)=yn(i).*(1-beta)+yo(j).*beta+alpha.*(rand-0.5);
endend % end for j
end % end for i
[xn,yn]=findrange(xn,yn,range);% Reduce the randomness during iterations（减少迭代过程中的随机性）
function alpha=newalpha(alpha,delta)
alpha=alpha*delta;% Make sure the fireflies are within the range（确保萤火虫在范围内）
function [xn,yn]=findrange(xn,yn,range)
for i=1:length(yn),if xn(i)<=range(1), xn(i)=range(1); endif xn(i)>=range(2), xn(i)=range(2); endif yn(i)<=range(3), yn(i)=range(3); endif yn(i)>=range(4), yn(i)=range(4); end
end
%  ============== end =====================================

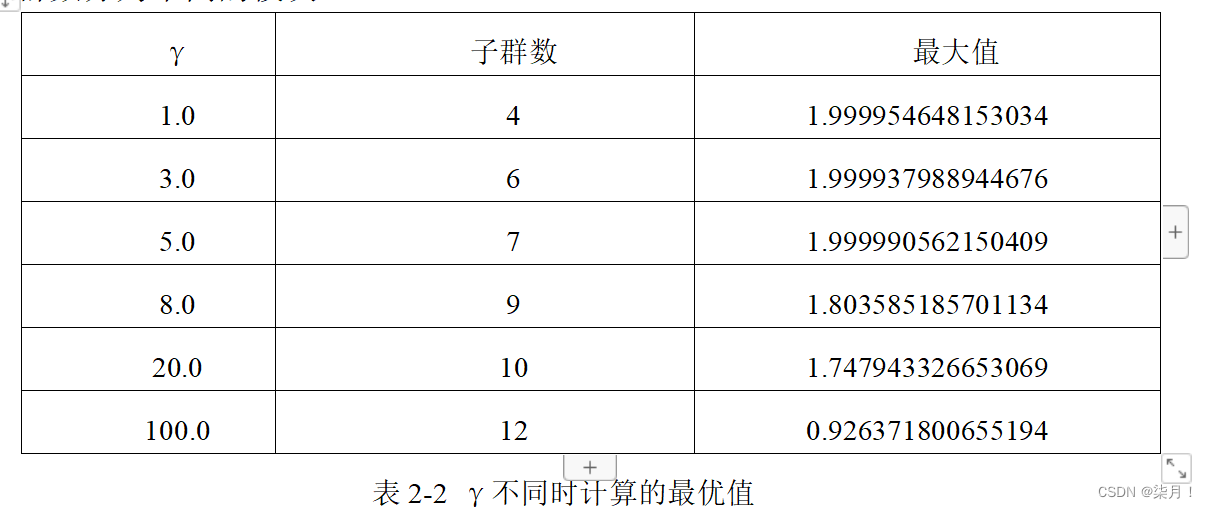
当γ取不同值时，子群的规模大小如下：

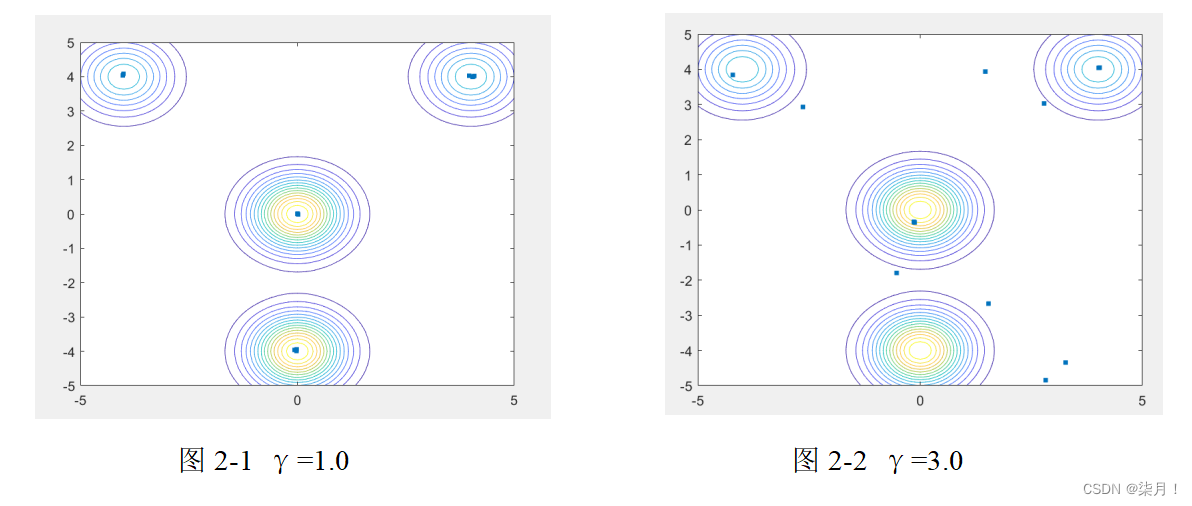
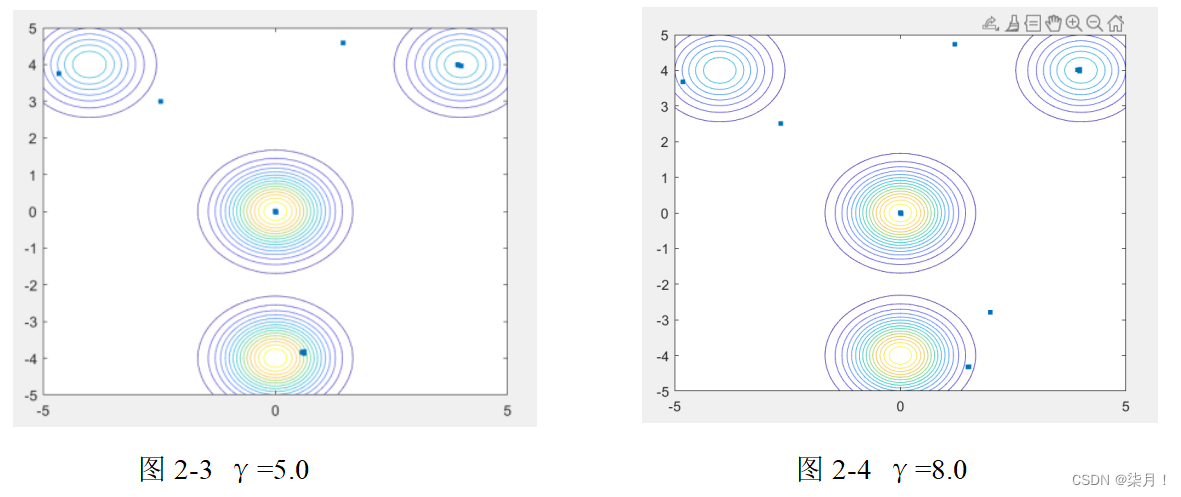
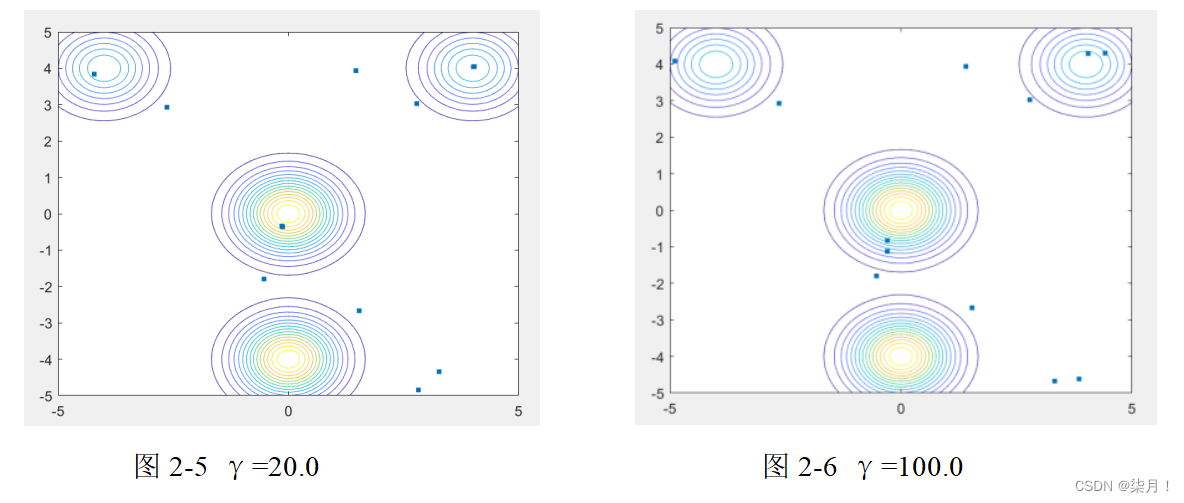
总结：光吸收系数γ对萤火虫算法性能的影响非常大。此参数不仅可以使整个种群自动分成子种群并行寻优，还能有效的平衡算法的全局探测和局部挖掘的能力。光吸收系数γ的优化设置还取决于待求解问题的类型，并没有一个普适性的取值。

2.最大吸引力 $\beta _{0}$ 对算法性能的影响

$\beta _{0}$ 为最大吸引力，即萤火虫在光源处（r=0 处）的吸引力大小。萤火虫算法位置移动公式吸引力项中参数高鲁棒性参数，对算法性能影响较小。因此在实际应用中可以取为 $\beta _{0}$ =1。

3.随机项系数 $\alpha$ 对算法性能的影响

式（2-6）位置更新公式中第三项为随机移动项。理论上，随机项系数 $\alpha$ 的步长对算法的执行效率影响较大。对于固定次数的迭代，决定了随机游走的长度。显然，如果取值过大，新产生的解与上一步迭代产生的解之间的距离将会过远，使算法搜索过于跳跃而缺乏规律性；如果取值过小，两次迭代的位置变化将会过小而不容易被察觉，从而使算法的搜索过程消耗过多的时间。这两种情况都是不可取的。

因此在算法实现中，通常要求在算法迭代初期种群中的萤火虫拥有较大的移动步长以提高算法的全局探测能力；而在算法迭代后期种群中的萤火虫拥有较小的移动步长以提高算法的局部挖掘能力，在最优解附近进行精细化的搜索。

2.5 萤火虫算法的时间复杂度分析

萤火虫算法在程序实现过程中含有一个基于算法迭代次数t 的外部循环和两个基于种群数量n 的内部循环，所以算法的时间复杂度的极限形式为 O( $n^{2}t$ )。由于在实际运行中，种群大小n一般取值较小（如n=20-40），而算法的迭代次数t一般取值较大（如t =2000-10000），因此可以将萤火虫算法的时间复杂度看成是算法的迭代次数t的线性函数。另外，对于萤火虫算法，如果种群大小n 取一非常大的值时，为了减少算法的时间复杂度，可以对所有萤火虫的亮度和吸引力进行排序，以减少一个内部循环。此时萤火虫算法的时间复杂度将变为O(ntlogn)。

2.6 萤火虫算法的有效性分析

除了与其他群智能优化算法类似的属性、优势外，萤火虫算法还具有三个特有的优势：

第一，萤火虫算法含有随距离增加而递减的吸引力，这种机制可以使种群在迭代过程中自动的分成几个子种群，子种群在某个模态或者局部最优值附近移动（种群在迭代过程中可以自动的分成多个子种群进行并行寻优）。

第二，如果粒子的数量远远多于待优化问题的模态数量时，这种种群的自动分组机制可以保证算法同时搜索到待优化问题的所有的优化解（具有解决多模态问题的机制）。

第三，萤火虫算法位置移动公式中随机项参数可以控制算法在迭代过程中随机机制的大小，因此优化随机项参数的选取可以加快算法的收敛效率（在求解过程中具有遍历性和多样性）。

3.萤火虫算法的应用

近年来，萤火虫算法被广泛地应用解决不同领域的实际优化问题，本部分对目前萤火虫算法的一些典型应用进行综述。

经济负荷分配问题是一种约束优化问题，指在满足电力系统或发电机组运行约束条件的基础上在各台机组间合理地分配负荷以达到最小化发电成本的目的。针对此问题，Yang[9]等基于简单的约束处理法则，构造了一种求解新型萤火虫算法。Chen[10]等提出了一种改进的萤火虫算法，该方法引入了 3 种策略: (1)利用萤火虫之间的距离信息自适应调节光吸收系数; (2) 应用递减策略调整步长因子; (3) 引入杂交操作保持种群多样性。

Kazem[11]等在萤火虫算法的基础上引入了混沌映射函数和支持向量回归，并将其应用于股票价格预测。Zhang[12]等也提出了一种基于支持向量回归的萤火虫算法。针对城市未来水资源需求预测问题，Wang[13]等提出了一种动态萤火虫预测算法。该方法以城市历史人口、经济和水量需求数据为基础，构造了线性、指数和混合预测模型，然后利用改进的萤火虫算法的对预测模型进行优化以确定模型参数。针对现有 PM2.5 浓度预测误差较大的问题，范文婷[14]等提出了一种基于支持向量机的萤火虫预测算法。该方法引入邻域搜索和可变步长策略以改进萤火虫算法性能，利用萤火虫算法优化 SVM 的参数，然后使用最优参数 SVM 模型预测太原市 PM2.5值。

针对多目标水资源优化配置问题，赵燕[15]等通过线性加权法将多目标模型化为单目标模型，在萤火虫算法的基础上引入一种自适应型惯性权重，将固定步长改进为可变步长，求解优化配置模型。Wang[16]等提出了一种混合多目标萤火虫算法，以经济、社会、环境综合效益为优化目标进行水资源配置。杨旺旺[17]等在标准萤火虫算法的基础上，引入了隔代大步长纯随机游走、优势保留和变异机制等策略。以发电量最大为目标，应用改进的萤火虫算法优化黑河梯级水电站群。针对时间和可靠性双重约束下费用最小化的云工作流调度问题，郑宏升[18]等提出基于萤火虫算法和动态优先级的最优调度方案。结合云工作流调度问题的特点，重新定义了萤火虫算法中的位置、距离以及位置更新方式，同时对于每一种调度方案，采用动态优先级算法确定任务顺序，以减少工作流完成时间。针对薄膜晶体管液晶显示器装配调度问题，李瑞婷[19]等以最小化工件最大完工时间和加权延迟最小为调度目标，建立了装配作业调度模型。在标准萤火虫算法的基础上，引入混沌搜索以克服了算法易陷入局部最优、优化速度慢以及计算量大等缺点。此外，萤火虫算法还被应用于车间调度、供应链优化、物流调度等问题。

针对特征提取问题，Zhang[20]等提出了一种基于距离的离散萤火虫算法。该方法对光吸收系数和步长因子进行动态更新，并构造了一种交互信息准则来提高算法的效率。Xu[21]等基于二进制萤火虫算法和反向学习策略，提出了另外一种特征提取算法。文献[22]也构造了一种二进制萤火虫特征提取算法，该方法引入了退货成本策略以防止算法过早收敛。此外，萤火虫算法还被应用于分类、聚类等问题。

在图像处理领域，萤火虫算法获得了较好的应用，如图像水印技术[23]、盲图像隐写分析[24]、图像分割[25]、图像压缩[26]、视频跟踪[27]等。在工程设计领域，萤火虫算法也能取得较好的效果，如结构设计[28]、管网优化设计[29]、滤波器设计[30]、网络设计[31]等。

参考文献：张丽娜. 萤火虫算法研究及其在船舶运动参数辨识中的应用[D]. 哈尔滨工程大学.