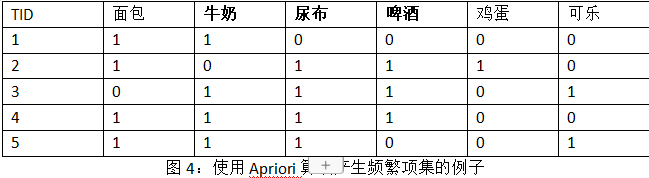
挖掘强关联规则的过程:
1.得到最大频繁项目集(这里使用apriori算法)
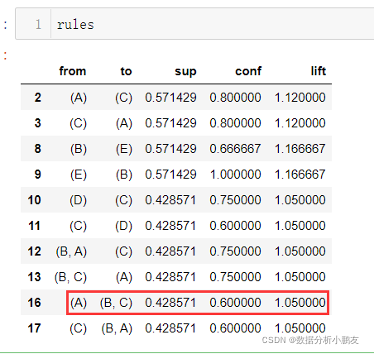
2.在最大频繁项目集中找强关联规则
工程结构:

(把下面的文件放到自己建的工程中就可以运行了,如果嫌麻烦的话把这些都放到main.cpp中也可以,建议分开放。但是要注意代码中有一个地方用到了自动数据类型auto,要开c++11,否则编译会报错,如果没开的话按照代码注释改一下就可以了。)
codeblock中开c++11:
settings->compiler:

运行结果:

含的文件:
(代码中都有注释,很容易看懂的)
mian.cpp
#include "mining.h"
int main()
{//freopen("in.txt","r",stdin);PSet D; //int min_support,num;cout<<"输入最小支持度和事务个数:"<<endl;cin>>min_support>>num;cout<<"输入所有事务"<<endl;for(int i=0;i<num;i++){ItemSet tem;cin>>tem.items;tem.cnt=1;D.push_back(tem);}//得到频繁项目集PSet result=apriori(D,min_support);cout<<endl<<"所有的频繁项目集:"<<endl<<'{';for(int i=0;i<result.size();i++)i==result.size()-1?cout<<result[i].items<<'}'<<endl:cout<<result[i].items<<',';//得到最大频繁项目集result=get_max(result);cout<<endl<<"最大频繁项目集:"<<endl<<'{';for(int i=0;i<result.size();i++)i==result.size()-1?cout<<result[i].items<<'}'<<endl:cout<<result[i].items<<',';cout<<endl;double min_conf;cout<<"输入最小置信度:";cin>>min_conf;//找强关联规则RuleSet rules=find_rules(D,result,min_conf);cout<<endl<<"满足条件的所有强关联规则(后面两个分别是置信度和支持度):"<<endl;for(int i=0;i<rules.size();i++)cout<<rules[i].f<<"->"<<rules[i].t<<" "<<rules[i].conf<<" "<<rules[i].support<<endl;return 0;
}
mining.h
#include "base.h"
#include "apriori.h"
#include "gen.h"
base.h
#include <bits/stdc++.h>
using namespace std;//项集的数据结构
struct ItemSet
{string items;int cnt;bool operator <(ItemSet t)const{if(items==t.items)return cnt<t.cnt;return items<t.items;}bool operator ==(ItemSet t)const{return items==t.items&&cnt==t.cnt;}
};//规则的数据结构
struct Rule
{string f,t;double support,conf;bool operator ==(Rule x)const{return f==x.f&&t==x.t&&support;}bool operator <(Rule x)const{if(f==x.f)return t<x.t;else return f<x.f;}
};//项目集的数据类型
typedef vector<ItemSet> PSet;//规则集合
typedef vector<Rule> RuleSet;//判断a中有多少个项目不属于b,显然当返回值是0的时候a是b的自子集
//gen.h和apriori.h中都会用到
int belong(string a,string b)
{int ct=0;for(int i=0;i<a.length();i++)if(b.find_first_of(a[i])==string::npos)ct++;return ct;
}
apriori.h
//apriori算法初始时用到,获得L1
PSet get(PSet &D)
{set<char> se;PSet ans;for(int i=0;i<D.size();i++){for(int j=0;j<D[i].items.length();j++)se.insert(D[i].items[j]);}auto it=se.begin();//如果没有开c++11标准的话,把auto改为set<char>::iteratorwhile(it!=se.end()){ItemSet tem;tem.cnt=0;tem.items.push_back(*it);ans.push_back(tem);it++;}return ans;
}//将b加到a中,用于将apriori中产生的Li加入到最后的结果中
void con(PSet &a,PSet &b)
{for(int i=0;i<b.size();i++)a.push_back(b[i]);
}//生成候选集时用到,根据a和b生成一个候选项集
string gen(string a,string b)
{sort(a.begin(),a.end());sort(b.begin(),b.end());for(int i=0;i<a.length();i++){if(b.find_first_of(a[i])==string::npos){b.push_back(a[i]);sort(b.begin(),b.end());return b;}}
}//get_candidates中会用到的函数,判断items是否包含非频繁项目集
bool contain_inf(PSet &Li,string items)
{for(int i=0;i<items.length();i++){string tem=items;tem.erase(tem.begin()+i);bool flag=false;for(int j=0;j<Li.size();j++){if(!belong(tem,Li[j].items)){flag=true;break;}}if(!flag)return 1;}return 0;
}//在频繁项目集中求最大频繁项目集
PSet get_max(PSet &L)
{PSet ans;for(int i=0;i<L.size();i++){bool flag=false;for(int j=0;j<L.size();j++)if(i!=j&&!belong(L[i].items,L[j].items)){flag=true;break;}if(!flag)ans.push_back(L[i]);}return ans;
}//apriori算法要用到的函数,根据Li(每个项集都是k项)生成候选项目集Ci(每个项集都是k+1项)
PSet get_candidates(PSet &Li)
{PSet Ci;for(int i=0;i<Li.size();i++){for(int j=i+1;j<Li.size();j++){if(i!=j&&belong(Li[i].items,Li[j].items)==1){ItemSet tem;tem.cnt=0;tem.items=gen(Li[i].items,Li[j].items);if(!contain_inf(Li,tem.items))Ci.push_back(tem);}}}sort(Ci.begin(),Ci.end());Ci.erase(unique(Ci.begin(),Ci.end()),Ci.end());return Ci;
}//apriori算法主体,求频繁项目集
PSet apriori(PSet &D,int min_support)
{PSet Ci,Li,L;Li=get(D);while(true){con(L,Li);Ci=get_candidates(Li);for(int i=0;i<Ci.size();i++){for(int j=0;j<D.size();j++)if(!belong(Ci[i].items,D[j].items))Ci[i].cnt++;}Li.clear();for(int i=0;i<Ci.size();i++)if(Ci[i].cnt>=min_support)Li.push_back(Ci[i]);if(Li.size()==0)break;}return L;
}
gen.h
//求差集b-a
string inter(string a,string b)
{int pos;for(int i=0;i<a.length();i++){pos=b.find_first_of(a[i]);if(pos!=string::npos)b.erase(b.begin()+pos);}return b;
}//将b中的规则加到a中
void con_rule(RuleSet &a,RuleSet &b)
{for(int i=0;i<b.size();i++)a.push_back(b[i]);
}//求a的支持数(这里只能说是支持度,因为并没有除总事务的个数)
double support(PSet &D,ItemSet a)
{double conf=0;for(int i=0;i<D.size();i++)if(!belong(a.items,D[i].items))conf++;return conf;
}RuleSet gen_rules(PSet &D,ItemSet Li,ItemSet Lm,double min_conf)
{double conf;RuleSet rules;for(int i=0;i<Lm.items.length();i++){ItemSet tem=Lm;tem.items.erase(tem.items.begin()+i);conf=(double)Li.cnt/support(D,tem);if(conf>min_conf){Rule rule;rule.f=tem.items;rule.t=inter(tem.items,Li.items);rule.conf=conf;rules.push_back(rule);}if(tem.items.length()>1){RuleSet rules2=gen_rules(D,Li,tem,min_conf);con_rule(rules,rules2);}}sort(rules.begin(),rules.end());rules.erase(unique(rules.begin(),rules.end()),rules.end());return rules;
}RuleSet find_rules(PSet &D,PSet &L,double min_conf)
{RuleSet rules;for(int i=0;i<L.size();i++){RuleSet tem=gen_rules(D,L[i],L[i],min_conf);con_rule(rules,tem);}sort(rules.begin(),rules.end());rules.erase(unique(rules.begin(),rules.end()),rules.end());return rules;
}