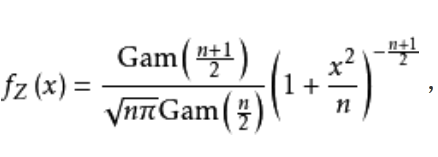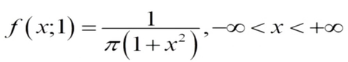Hello，大家好！最近有在学习一些有关偏态分布的数理知识，但在搜偏$t$分布的相关资料的时候感觉比较散，所以做个整理，主要参考的书籍是Azzalini在2014年出版的一本有关偏态分布族的书《The Skew-Normal and Related Families》，大家可以文末获取，有哪里理解不对的地方，还请各位大佬多多指正。

偏$t$分布定义

偏$t$分布的生成，可以通过调节$t$分布的尾部厚度来实现，那么我们先来写下$t$分布的概率密度函数
$$t(x;\nu )=\frac{\Gamma (\frac{\nu +1}{2})}{\sqrt{\pi \nu }\Gamma (\frac{\nu }{2})}(1+\frac{x^2}{\nu }{)}^{-\frac{\nu +1}{2}},x\in \mathbb{R},$$
其中，$\nu$代表自由度。

性质1.1： 用$f_0$表示${\mathbb{R}}^d$上的概率密度函数，用$G(\cdot )$表示一个连续分布函数，用$w(\cdot )$表示${\mathbb{R}}^d$上的实值函数，使得
$$f_0(-x)=f_0(x),w(-x)=-w(x),G_0(-y)=1-G_0(y)$$
对于$x\in {\mathbb{R}}^d$，$y\in \mathbb{R}$，则
f ( x ) = 2 f 0 ( x ) G { w ( x ) } f(x)=2f_0(x)G\{ w(x)\} f(x)=2f0​(x)G{w(x)}
表示为${\mathbb{R}}^d$上的概率密度函数。

那么对于$t$分布，我们就可以通过性质1.1来生成尾部厚度不一的偏$t$分布，根据以往的研究，以线性形式来引入不对称的版本，即
$$2t(x;\nu )T(\alpha x;\nu )$$
其中，$T(\cdot ;\nu )$表示$t$分布的累积分布函数，$\alpha$表示偏度参数。

除了这种构建方式外，还可以通过类似于$t$分布随机变量的构建方式来获得，并且这种方式更被普遍引用，同样，我们先写出$t$分布的随机变量
$$Z=\frac{Z_0}{\sqrt{V}},$$
其中，$Z_0\sim \mathrm{N}(0,1)$和$V\sim {\chi }_{\nu }^2/\nu$为独立随机变量。

相应地，通过将$Z_0$的正态分布假设替换为$Z_0\sim \mathrm{S}\mathrm{N}(0,1,\alpha )$来获得偏$t$分布的公式。在这种情况下，若$h(\cdot )$表示$V$的密度函数，则随机变量$Z$的密度函数为
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ t(x;\alpha,\nu…
便得到了$Z\sim \mathrm{S}\mathrm{T}(0,1,\alpha ,\nu )$，如果$\alpha =0$，那么该密度函数便会变回常规的学生$t$分布；如果$\nu \to \infty$，则变回$\mathrm{S}\mathrm{N}(0,1,\alpha )$密度函数。

为了更广泛的使用，我们需要让该分布再包含位置参数和尺度参数来进一步推广偏$t$分布。我们令$Y=\xi +\omega Z$，那么原来关于$x$的概率密度函数$t(x;\alpha ,\nu )$，变为了${\omega }^{-1}t(z;\alpha ,\nu )$，其中$z={\omega }^{-1}(x-\xi )$，这样就得到含有均值、方差、偏度、自由度四个参数的偏$t$分布$Y\sim \mathrm{S}\mathrm{T}(\xi ,{\omega }^2,\alpha ,\nu )$，即
$$f_{ST}(y)=\frac{2}{\omega }t(\eta ;\nu )T(\alpha \eta \sqrt{\frac{\nu +1}{\nu +{\eta }^2}};\nu +1),\eta =\frac{y-\xi }{\omega }$$

---

（先整理了定义，后续再逐步更新相关性质，未完待续…）

资源获取

• 关注公众号，回复“偏t分布”，获得电子书。