•  什么是关联规则

         关联规则（Association Rules）是反映一个事物与其他事物之间的相互依存性和关联性，是数据挖掘的一个重要技术，用于从大量数据中挖掘出有价值的数据项之间的相关关系。

         所谓数据挖掘就是以某种方式分析源数据，从中发现一些潜在的有用的信息 。即数据挖掘又可以称作知识发现，而机器学习算法则是这种“某种方式”。

         举个简单的例子（尿布和啤酒太经典）：通过调研超市顾客购买的东西，可以发现30%的顾客会同时购买床单和枕套，而在购买床单的顾客中有80%的人购买了枕套，这就存在一种隐含的关系：床单→枕套，也就是说购买床单的顾客会有很大可能购买枕套，因此商场可以将床单和枕套放在同一个购物区，方便顾客购买。

• 关联规则中的概念

  • 项目：交易数据库中的一个字段，对超市的交易来说一般是指一次交易中的一个物品，如：牛奶

  • 事务：某个客户在一次交易中，发生的所有项目的集合，如（牛奶，面包，啤酒）

  • 项集：包含若干个项目的集合（一次事务中的），一般会大于0个

  • 支持度（Support）：项集（X，Y）在总项集中出现的概率

  • 频繁项集（Frequent item Sets）：某个项集的支持度大于设定阈值（人为设定或者根据数据分布或者经验来设定），即称这个项集为频繁项集

  • 置信度（Confidence）：在先决条件X发生的条件下，由关联规则（X->Y）推出Y的概率

  • 提升度：表示含有X的条件下同事含有Y的概率，与无论含不含有Y的

支持度与置信度的例子：

         假如有一条规则：牛肉—>鸡肉，那么同时购买牛肉和鸡肉的顾客比例是3/7，而购买牛肉的顾客当中也购买了鸡肉的顾客比例是3/4。这两个比例参数是很重要的衡量指标，它们在关联规则中称作支持度（support）和置信度（confidence）。对于规则：牛肉—>鸡肉，它的支持度为3/7，表示在所有顾客当中有3/7同时购买牛肉和鸡肉，其反应了同时购买牛肉和鸡肉的顾客在所有顾客当中的覆盖范围；它的置信度为3/4，表示在买了牛肉的顾客当中有3/4的人买了鸡肉，其反应了可预测的程度，即顾客买了牛肉的话有多大可能性买鸡肉。

         支持度：P（AUB），即A和B这两个项集在事务集D中同时出现的概率。

                                                 support（A=>B） = P（AUB）

         置信度：P（B|A），即在出现项集A的事务集D中，项集B也同时的概率。

                   

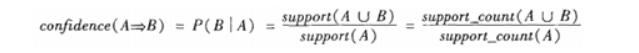
 设定合理的支持度和置信度

          对于某条规则：（A = a）−>（B = b）（support=30%,confident=60%）；其中support=30%表示在所有的数据记录中，同时出现A=a和B=b的概率为30%；confident=60%表示在所有的数据记录中，在出现A=a的情况下出现B=b的概率为60%，也就是条件概率。支持度揭示了A=a和B=b同时出现的概率，置信度揭示了当A=a出现时，B=b是否会一定出现的概率。

        （1）如果支持度和置信度闭值设置的过高，虽然可以减少挖掘时间，但是容易造成一些隐含在数据中非频繁特征项被忽略掉，难以发现足够有用的规则；

        （2）如果支持度和置信度闭值设置的过低，又有可能产生过多的规则，甚至产生大量冗余和无效的规则，同时由于算法存在的固有问题，会导致高负荷的计算量，大大增加挖掘时间。

Apriori算法简介

        Apriori算法：使用候选项集找频发项集

        Apriori算法是一种罪有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于两阶段频集思想的递推算法。该关联规则在分类上属于单维、单层、布尔关联规则。在这里，所有支持度大于最小支持度的项集称为频繁项集，简称频集。

Apriori原理：如果某个项集是频繁的，那么它的所有子集也是频繁的。该定理的逆反定理为：如果某一个项集是非频繁的，那么它的所有超集（包含该集合的集合）也是非频繁的。Apriori原理的出现，可以在得知某些项集是非频繁之后，不需要计算该集合的超集，有效地避免项集数目的指数增长，从而在合理时间内计算出频繁项集。

在图中，已知阴影项集{2,3}是非频繁的。利用这个知识，我们就知道项集{0,2,3}，{1,2,3}以及{0,1,2,3}也是非频繁的。也就是说，一旦计算出了{2,3}的支持度，知道它是非频繁的后，就可以紧接着排除{0,2,3}、{1,2,3}和{0,1,2,3}。

算法思想

        ①找出所有的频集，这些项集出现的频繁性至少和预定义的最小支持度一样。

        ②由频集产生强关联规则，这些规则必须满足最小支持度和最小可信度。

        ③使用第1步找到的频集产生期望的规则，产生只包含集合的项的所有规则，其中每一条规则的右部只有一项，这里采用的是中规则的定义。

        ④一旦这些规则被生成，那么只有那些大于用户给定的最小可信度的规则才被留下来。为了生成所有频集，使用了递推的方法。

           

算法步骤

      

代码实现

#Apriori算法实现
from numpy import *def loadDataSet():return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]# 获取候选1项集，dataSet为事务集。返回一个list，每个元素都是set集合
def createC1(dataSet):C1 = []   # 元素个数为1的项集（非频繁项集，因为还没有同最小支持度比较）for transaction in dataSet:for item in transaction:if not [item] in C1:C1.append([item])C1.sort()  # 这里排序是为了，生成新的候选集时可以直接认为两个n项候选集前面的部分相同# 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在，所以要将候选1项集的每一个元素都转化为一个单独的集合。return list(map(frozenset, C1))   #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合（frozenset，Python中的数据结构）# 找出候选集中的频繁项集
# dataSet为全部数据集，Ck为大小为k（包含k个元素）的候选项集，minSupport为设定的最小支持度
def scanD(dataSet, Ck, minSupport):ssCnt = {}   # 记录每个候选项的个数for tid in dataSet:for can in Ck:if can.issubset(tid):ssCnt[can] = ssCnt.get(can, 0) + 1   # 计算每一个项集出现的频率numItems = float(len(dataSet))retList = []supportData = {}for key in ssCnt:support = ssCnt[key] / numItemsif support >= minSupport:retList.insert(0, key)  #将频繁项集插入返回列表的首部supportData[key] = supportreturn retList, supportData   #retList为在Ck中找出的频繁项集（支持度大于minSupport的），supportData记录各频繁项集的支持度# 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。
def aprioriGen(Lk, k):retList = []lenLk = len(Lk)for i in range(lenLk):for j in range(i + 1, lenLk):# 前k-1项相同时，才将两个集合合并，合并后才能生成k+1项L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]   # 取出两个集合的前k-1个元素L1.sort(); L2.sort()if L1 == L2:retList.append(Lk[i] | Lk[j])return retList# 获取事务集中的所有的频繁项集
# Ck表示项数为k的候选项集，最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集，supK为其支持度，Lk和supK由scanD()函数通过Ck计算而来。
def apriori(dataSet, minSupport=0.5):C1 = createC1(dataSet)  # 从事务集中获取候选1项集D = list(map(set, dataSet))  # 将事务集的每个元素转化为集合L1, supportData = scanD(D, C1, minSupport)  # 获取频繁1项集和对应的支持度L = [L1]  # L用来存储所有的频繁项集k = 2while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集Ck = aprioriGen(L[k-2], k)   # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集Lk, supK = scanD(D, Ck, minSupport)  # Lk表示项数为k的频繁项集，supK为其支持度L.append(Lk);supportData.update(supK)  # 添加新频繁项集和他们的支持度k += 1return L, supportDataif __name__=='__main__':dataSet = loadDataSet()  # 获取事务集。每个元素都是列表# C1 = createC1(dataSet)  # 获取候选1项集。每个元素都是集合# D = list(map(set, dataSet))  # 转化事务集的形式，每个元素都转化为集合。# L1, suppDat = scanD(D, C1, 0.5)# print(L1,suppDat)L, suppData = apriori(dataSet,minSupport=0.7)print(L,suppData)

 

FP-growth算法

         Apriori算法是关联规则的基本算法，很多用于发现关联规则的算法都是基于Apriori算法，但Apriori算法需要多次访问数据库，具有严重的性能问题。FP-Growth算法只需要两次扫描数据库，相比于Apriori减少了I/O操作，克服了Apriori算法需要多次扫描数据库的问题。

        算法步骤：

1. 构建FP树

2. 从FP树中挖掘频繁项集

        实现流程：

第一步：创建FP树

 

第二步：挖掘频繁项集

代码实现：

# FP树类
class treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValue  #节点元素名称，在构造时初始化为给定值self.count = numOccur   # 出现次数，在构造时初始化为给定值self.nodeLink = None   # 指向下一个相似节点的指针，默认为Noneself.parent = parentNode   # 指向父节点的指针，在构造时初始化为给定值self.children = {}  # 指向子节点的字典，以子节点的元素名称为键，指向子节点的指针为值，初始化为空字典# 增加节点的出现次数值def inc(self, numOccur):self.count += numOccur# 输出节点和子节点的FP树结构def disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)# =======================================================构建FP树==================================================# 对不是第一个出现的节点，更新头指针块。就是添加到相似元素链表的尾部
def updateHeader(nodeToTest, targetNode):while (nodeToTest.nodeLink != None):nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNode# 根据一个排序过滤后的频繁项更新FP树
def updateTree(items, inTree, headerTable, count):if items[0] in inTree.children:# 有该元素项时计数值+1inTree.children[items[0]].inc(count)else:# 没有这个元素项时创建一个新节点inTree.children[items[0]] = treeNode(items[0], count, inTree)# 更新头指针表或前一个相似元素项节点的指针指向新节点if headerTable[items[0]][1] == None:  # 如果是第一次出现，则在头指针表中增加对该节点的指向headerTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1:# 对剩下的元素项迭代调用updateTree函数updateTree(items[1::], inTree.children[items[0]], headerTable, count)# 主程序。创建FP树。dataSet为事务集，为一个字典，键为每个事物，值为该事物出现的次数。minSup为最低支持度
def createTree(dataSet, minSup=1):# 第一次遍历数据集，创建头指针表headerTable = {}for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + dataSet[trans]# 移除不满足最小支持度的元素项keys = list(headerTable.keys()) # 因为字典要求在迭代中不能修改，所以转化为列表for k in keys:if headerTable[k] < minSup:del(headerTable[k])# 空元素集，返回空freqItemSet = set(headerTable.keys())if len(freqItemSet) == 0:return None, None# 增加一个数据项，用于存放指向相似元素项指针for k in headerTable:headerTable[k] = [headerTable[k], None]  # 每个键的值，第一个为个数，第二个为下一个节点的位置retTree = treeNode('Null Set', 1, None) # 根节点# 第二次遍历数据集，创建FP树for tranSet, count in dataSet.items():localD = {} # 记录频繁1项集的全局频率，用于排序for item in tranSet:if item in freqItemSet:   # 只考虑频繁项localD[item] = headerTable[item][0] # 注意这个[0]，因为之前加过一个数据项if len(localD) > 0:orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] # 排序updateTree(orderedItems, retTree, headerTable, count) # 更新FP树return retTree, headerTable# =================================================查找元素条件模式基===============================================# 直接修改prefixPath的值，将当前节点leafNode添加到prefixPath的末尾，然后递归添加其父节点。
# prefixPath就是一条从treeNode（包括treeNode）到根节点（不包括根节点）的路径
def ascendTree(leafNode, prefixPath):if leafNode.parent != None:prefixPath.append(leafNode.name)ascendTree(leafNode.parent, prefixPath)# 为给定元素项生成一个条件模式基（前缀路径）。basePet表示输入的频繁项，treeNode为当前FP树中对应的第一个节点
# 函数返回值即为条件模式基condPats，用一个字典表示，键为前缀路径，值为计数值。
def findPrefixPath(basePat, treeNode):condPats = {}  # 存储条件模式基while treeNode != None:prefixPath = []  # 用于存储前缀路径ascendTree(treeNode, prefixPath)  # 生成前缀路径if len(prefixPath) > 1:condPats[frozenset(prefixPath[1:])] = treeNode.count  # 出现的数量就是当前叶子节点的数量treeNode = treeNode.nodeLink  # 遍历下一个相同元素return condPats# =================================================递归查找频繁项集===============================================
# 根据事务集获取FP树和频繁项。
# 遍历频繁项，生成每个频繁项的条件FP树和条件FP树的频繁项
# 这样每个频繁项与他条件FP树的频繁项都构成了频繁项集# inTree和headerTable是由createTree()函数生成的事务集的FP树。
# minSup表示最小支持度。
# preFix请传入一个空集合（set([])），将在函数中用于保存当前前缀。
# freqItemList请传入一个空列表（[]），将用来储存生成的频繁项集。
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):# 对频繁项按出现的数量进行排序进行排序sorted_headerTable = sorted(headerTable.items(), key=lambda p: p[1][0])  #返回重新排序的列表。每个元素是一个元组，[（key,[num,treeNode],()）bigL = [v[0] for v in sorted_headerTable]  # 获取频繁项for basePat in bigL:newFreqSet = preFix.copy()  # 新的频繁项集newFreqSet.add(basePat)     # 当前前缀添加一个新元素freqItemList.append(newFreqSet)  # 所有的频繁项集列表condPattBases = findPrefixPath(basePat, headerTable[basePat][1])  # 获取条件模式基。就是basePat元素的所有前缀路径。它像一个新的事务集myCondTree, myHead = createTree(condPattBases, minSup)  # 创建条件FP树if myHead != None:# 用于测试print('conditional tree for:', newFreqSet)myCondTree.disp()mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)  # 递归直到不再有元素# 生成数据集
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDat# 将数据集转化为目标格式
def createInitSet(dataSet):retDict = {}for trans in dataSet:retDict[frozenset(trans)] = 1return retDictif __name__=='__main__':minSup =3simpDat = loadSimpDat()  # 加载数据集initSet = createInitSet(simpDat)  # 转化为符合格式的事务集myFPtree, myHeaderTab = createTree(initSet, minSup)  # 形成FP树# myFPtree.disp()  # 打印树freqItems = []  # 用于存储频繁项集mineTree(myFPtree, myHeaderTab, minSup, set([]), freqItems)  # 获取频繁项集print(freqItems)  # 打印频繁项集