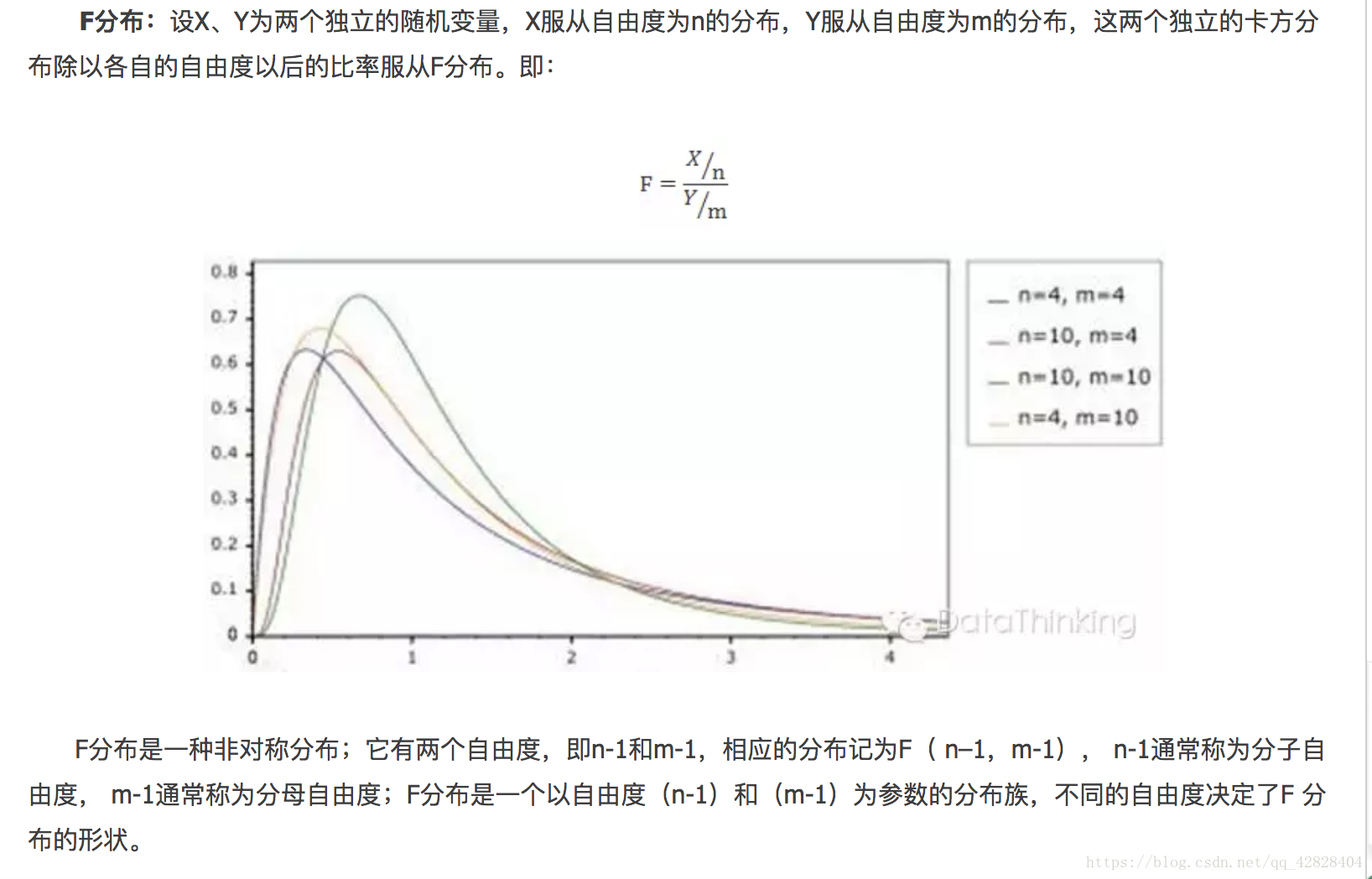
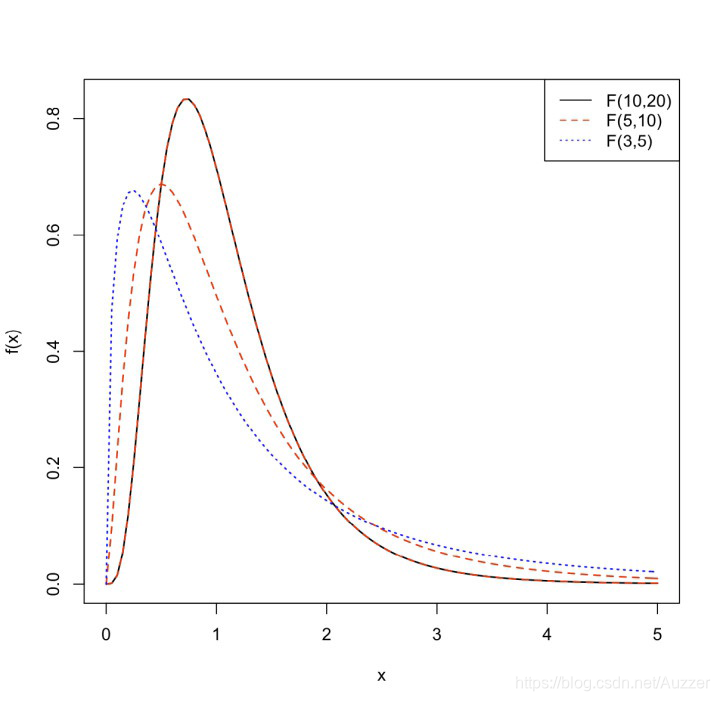
文章目录
- 一、基本概念
- 定义1. 记录(事务)
- 定义2. 事务集
- 定义3. 项目(项)
- 定义4. 项目集(项集)
- 定义5. k项集
- 定义6. 支持度(Support)
- 定义7. 置信度(Confidence)
- 定义8. 最小支持度(min Support)
- 定义9. 最小置信度(min Confidence)
- 定义10. 提升度
- 定义11. 频繁K项集
- 定义12. 候选K项集
- 定理1
- 定理2
- 二、Apriori 算法流程
- 三、Apriori 算法小案例
- 四、python 实战
一、基本概念
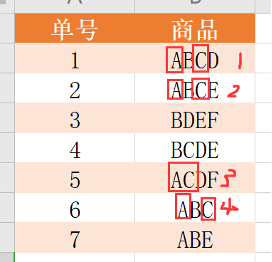
- 例表

定义1. 记录(事务)
- 如 {ABCD}, {ABCE}, … 每一个都是一条记录(事务)
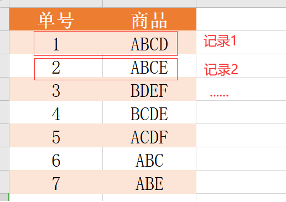
定义2. 事务集
- 如表,{ABCD,ABCE,…} 所有记录构成的集合叫做事务集
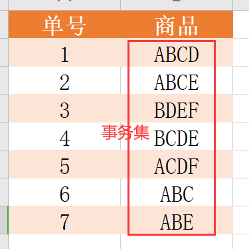
定义3. 项目(项)
- A、B、C … 每一个都称为一个项目(项)
定义4. 项目集(项集)
- 由项目组成的集合,如{A,B,C,D}、 {A、B、C、E}
定义5. k项集
- 如{A,B,C,D} 称为4项集(k=4)
定义6. 支持度(Support)
- 简单理解就是概率(频率)
S u p = 某 个 项 集 在 事 物 集 出 现 的 次 数 事 物 集 总 的 记 录 个 数 Sup = \dfrac{某个项集在事物集出现的次数}{事物集总的记录个数} Sup=事物集总的记录个数某个项集在事物集出现的次数
例:如项集 {AC} ,其支持度 S u p { A C } = 4 7 = 0.57 \ Sup\left\{AC\right\} = \dfrac{4}{7} = 0.57 Sup{AC}=74=0.57
定义7. 置信度(Confidence)
- 简单理解就是条件概率: P ( Y ∣ X ) = P ( X Y ) P ( X ) \ P(Y|X) = \dfrac{P(XY)}{P(X)} P(Y∣X)=P(X)P(XY),即在X出现的条件下,Y出现的概率
C o n ( X → Y ) = S u p ( X Y ) S u p ( X ) \ Con(X\rightarrow Y) = \dfrac{Sup(XY)}{Sup(X)} Con(X→Y)=Sup(X)Sup(XY)
定义8. 最小支持度(min Support)
- 人为规定的一个支持度
定义9. 最小置信度(min Confidence)
- 人为规定的一个置信度
定义10. 提升度
L i f t ( A → B ) = c o n ( A → B ) s u p ( B ) \ Lift(A\rightarrow B) = \frac{con(A \rightarrow B)}{sup(B)} Lift(A→B)=sup(B)con(A→B)
在A发生的基础上发生B的概率与B单独发生的概率比值
定义11. 频繁K项集
- 满足最小支持度的K项集
- 假设给定最小支持度为0.5,2项集{AC}的支持度Sup{AC} = 0.57,则称{AC}为频繁2项集
定义12. 候选K项集
- 用来生成频繁K项集的K项集(不等价所有K项集)
定理1
- 如果X是一个频繁K项集,则它的所有子集也一定是频繁的
定理2
- 如果X不是K-1项频繁,则它一定不是频繁K项集
二、Apriori 算法流程
- Step 1:令K=1,计算单个项目的支持度,并筛选出频繁1项集(≥最小支持度)
- Step 2:从K=2开始)根据K-1项的频繁项目集生成候选K项目集,并进行预剪枝
- Step 3:由候选K项目集生成频繁K项集(筛选出满足最小支持度的K项集)
重复步骤2和3,直到无法满足最小支持度的集合。(第一阶段结束)
- Step 4:将获得的最终频繁K项集,依次取出,同时计算该次取出的这个K项集的所有真子集,然后以排列组合的方式形成关联规则,并计算规则的置信度以及提升度,将符合要求的关联规则生成提出。
三、Apriori 算法小案例

-
首先,给定
最小支持度: 0.3 = 2.1 7 \ 0.3 = \frac{2.1}{7} 0.3=72.1 -
Step 1:令K=1,计算单个项目的支持度,并筛选出频繁1项集(≥最小支持度)
{A},{B},{C},{D},{E},{F}的支持度分别为:0.71,0.86,0.71,0.57,0.57,0.29. {F}的支持度小于给定的最小支持度0.3,去掉,得到频繁1项集为{A},{B},{C},{D},{E} -
Step 2:从K=2开始)根据K-1项的频繁项目集生成候选K项目集,并进行预剪枝
用K-1项集进行排列组合(这里K-1=1,K=2)(这里没有用到预剪枝),得到候选2项集:
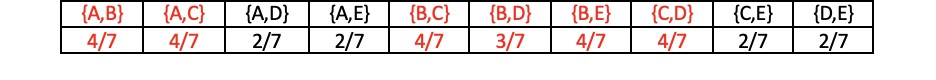
-
Step 3:由候选K项目集生成频繁K项集(筛选出满足最小支持度的K项集)
由最小支持度为2.1/7,可以筛选出频繁2项集:{A,B},{A,C},{B,C},{B,D},{B,E},{C,D} -
重复步骤2和3,直到无法满足最小支持度的集合:
重复第1次
(Step 2):根据频繁2项集,进行排列组合,生成候选3项集

(Step 3):首先将不满足K-1=2的项集删去,其次删去不满足最小支持度的项集(其实也可以用定理2,如项集{A,B,D},其K-1项子集{A,D}不是频繁2项集,故可以认为{A,B,D}也一定不是频繁项集)
最终得到的频繁3项集为:{A,B,C} ——(这里案例只有一个,实际情况可能很多)
- Step 4:将获得的最终频繁K项集,依次取出,同时计算该次取出的这个K项集的所有真子集,然后以排列组合的方式形成关联规则,并计算规则的置信度以及提升度,将符合要求的关联规则生成提出。
1)将获得的最终频繁K项集,依次取出:这里只有1个频繁K项集{A,B,C},故只取1次
2)计算该次取出的这个K项集的所有真子集.
{A,B,C}的所有真子集:{A},{B},{C},{AB},{AC},{BC}
3)以排列组合的方式形成关联规则(两个项集之间不能有交集)
{A}->{B}、 {A}->{C}、{A}->{BC}、
{B}->{A}、 {B}->{C}、{B}->{AC}、
{C}->{A}、 {C}->{B}、{C}->{AB}、
{AB}->{C}、{AC}->{B}、{BC}->{A}
4)计算规则的置信度以及提升度(以{A}->{BC}为例)
置信度: C o n ( { A } → { B , C } ) = S u p ( { B , C } ) S u p ( { A } ) = 3 / 5 = 0.6 \ Con(\left\{A\right\}→\left\{B,C\right\})=\frac{Sup(\left\{B,C\right\})}{Sup(\left\{A\right\})}=3/5=0.6 Con({A}→{B,C})=Sup({A})Sup({B,C})=3/5=0.6
提升度: L i f t ( { A } → { B , C } ) = C o n ( { A } → { B , C } ) S u p ( { B , C } ) = 0.6 / ( 4 / 7 ) = 1.05 > 1 \ Lift(\left\{A\right\}→\left\{B,C\right\})=\frac{Con(\left\{A\right\}→\left\{B,C\right\})}{Sup(\left\{B,C\right\})}=0.6/(4/7)=1.05>1 Lift({A}→{B,C})=Sup({B,C})Con({A}→{B,C})=0.6/(4/7)=1.05>1
因此{A}→{BC}是一条比较令人信服的关联规则
同理,计算其它关联规则的置信度和提升度即可。最后输出满足条件的关联规则。
四、python 实战
- 以上文数据集为例
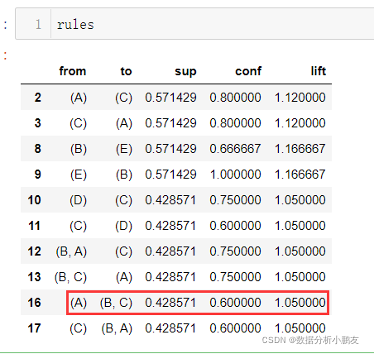
- 采用mlxtend库,没有安装的需要pip install mlxtend。最后的结果也表明,跟上文的结果一致。
- 参考:关联规则算法Apriori的Python实现
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules
import pandas as pd data_set = [['A','B','C','D'],['A','B','C','E'],['B','D','E','F'],['B','C','D','E'],['A','C','D','F'],['A','B','C'],['A','B','E']] #转换为算法可接受模型(布尔值)
te = TransactionEncoder()
df_tf = te.fit_transform(data_set)
df = pd.DataFrame(df_tf,columns=te.columns_) #设置支持度求频繁项集
frequent_itemsets = apriori(df,min_support=0.3,use_colnames= True)
#求关联规则,设置最小置信度为0.15
rules = association_rules(frequent_itemsets,metric = 'confidence',min_threshold = 0.15)
#设置最小提升度
rules = rules.drop(rules[rules.lift <1.0].index)
#设置标题索引并打印结果
rules.rename(columns = {'antecedents':'from','consequents':'to','support':'sup','confidence':'conf'},inplace = True)
rules = rules[['from','to','sup','conf','lift']]