Python实现关联规则推荐

1.什么关联规则
关联规则（Association Rules）是反映一个事物与其他事物之间的相互依存性和关联性，如果两个或多个事物之间存在一定的关联关系，那么，其中一个事物就能通过其他事物预测到。关联规则是数据挖掘的一个重要技术，用于从大量数据中挖掘出有价值的数据项之间的相关关系。

关联规则挖掘的最经典的例子就是沃尔玛的啤酒与尿布的故事，通过对超市购物篮数据进行分析，即顾客放入购物篮中不同商品之间的关系来分析顾客的购物习惯，发现美国妇女们经常会叮嘱丈夫下班后为孩子买尿布，30%-40%的丈夫同时会顺便购买喜爱的啤酒，超市就把尿布和啤酒放在一起销售增加销售额。有了这个发现后，超市调整了货架的设置，把尿布和啤酒摆放在一起销售，从而大大增加了销售额。

2.置信度与支持度
(1) 什么是规则？
规则形如"如果…那么…(If…Then…)"，前者为条件，后者为结果。例如一个顾客，如果买了可乐，那么他也会购买果汁。
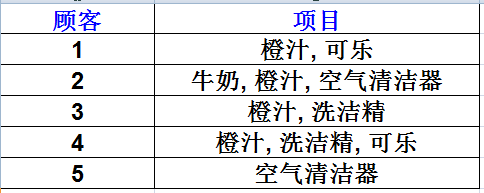
如何来度量一个规则是否够好？有两个量，置信度（Confidence）和支持度（Support），假如存在如下表的购物记录。

（2）在关联规则度量中有两个重要的度量值：支持度和置信度。
对于关联规则R:A=>B，则：
支持度（suppport）：是交易集中同时包含A和B的交易数与所有交易数之比。
Support(A=>B)=P(A∪B)=count(A∪B)/|D|
置信度（confidence）：是包含A和B交易数与包含A的交易数之比。
Confidence(A=>B)=P(B|A)=support(A∪B)/support(A)

(3) 支持度
支持度（Support）计算在所有的交易集中，既有A又有B的概率。例如在5条记录中，既有橙汁又有可乐的记录有2条。则此条规则的支持度为 2/5=0.4，即：
Support(A=>B)=P(AB)
现在这条规则可表述为，如果一个顾客购买了橙汁，则有50%(置信度)的可能购买可乐。而这样的情况（即买了橙汁会再买可乐）会有40%（支持度）的可能发生。

(4) 置信度
置信度（confidence）表示了这条规则有多大程度上值得可信。设条件的项的集合为A,结果的集合为B。置信度计算在A中，同时也含有B的概率（即：if A ,then B的概率）。即：
Confidence(A=>B)=P(B|A)
例如计算“如果Orange则Coke”的置信度。由于在含有“橙汁”的4条交易中，仅有2条交易含有“可乐”，其置信度为0.5。

(5) 最小支持度与频繁集
发现关联规则要求项集必须满足的最小支持阈值，称为项集的最小支持度（Minimum Support），记为supmin。支持度大于或等于supmin的项集称为频繁项集，简称频繁集，反之则称为非频繁集。通常k-项集如果满足supmin，称为k-频繁集，记作Lk。关联规则的最小置信度（Minimum Confidence）记为confmin，它表示关联规则需要满足的最低可靠性。

(6) 强关联规则
如果规则R：X=>Y 满足 support(X=>Y) >= supmin 且 confidence(X=>Y)>=confmin，称关联规则X=>Y为强关联规则，否则称关联规则X=>Y为弱关联规则。
在挖掘关联规则时，产生的关联规则要经过supmin和confmin的衡量，筛选出来的强关联规则才能用于指导商家的决策。

3.Python实现

测试数据集：

薯片,鸡蛋,面包,牛奶
薯片,鸡蛋,啤酒
面包,牛奶,啤酒
薯片,鸡蛋,面包,牛奶,啤酒
薯片,鸡蛋,面包
鸡蛋,面包,啤酒
薯片,面包,牛奶
薯片,鸡蛋,面包,牛奶
薯片,鸡蛋,牛奶

GUI.py实现GUI展示

# -*- coding: utf-8 -*-
import sys
from mylib import fp
import tkinter as tk
from tkinter import filedialog
from tkinter import scrolledtextclass GUI(object):#布局界面def __init__(self):#设置初始界面self.window=tk.Tk()self.window.title('关联规则挖掘系统')self.window.geometry('1150x550')#导入文件按钮self.botton1=tk.Button(self.window, text='导入文件',bg='green',fg='white',  font=('楷体', 12, 'bold'), width=8, height=1,command=self.openfile)self.botton1.place(x=70,y=60)#标签配置self.label2=tk.Label(self.window, text='最小支持数',bg='light blue',fg='white', font=('楷体', 16, 'bold'), width=10, height=1).place(x=10,y=160)self.label3=tk.Label(self.window, text='最小置信度',bg='light blue',fg='white', font=('楷体', 16, 'bold'), width=10, height=1).place(x=10,y=220)#导入文件内容的输出显示self.label4=tk.Label(self.window, text='导入文件内容如下',font=('楷体', 16, 'bold'), width=16, height=1).place(x=260,y=20)#创建结果显示框self.text1=scrolledtext.ScrolledText(self.window, height=28, width=23,font=('楷体', 13))self.text1.place(x=250,y=60)self.text1.bind("<Button-1>",self.clear)#各个频繁项集和强关联规则的输出显示self.label5=tk.Label(self.window, text='频繁项集和强关联规则',font=('楷体', 16, 'bold'), width=20, height=1).place(x=700,y=20)#创建结果显示框self.text2=scrolledtext.ScrolledText(self.window, height=28, width=60,font=('楷体', 10))self.text2.place(x=550,y=60)self.text2.bind("<Button-1>",self.clear)
#        self.text2.bind("<Button-1>",self.run)#显示导入文件的路径self.var0=tk.StringVar()self.entry1=tk.Entry(self.window, show=None, width='25', font=('Arial', 10), textvariable=self.var0)self.entry1.place(x=10,y=100)#自行设置最小支持度计数值,默认为0.5self.var1=tk.StringVar()self.var1.set('3')self.entry2=tk.Entry(self.window, show=None, width='3', font=('Arial', 16), textvariable=self.var1)self.entry2.place(x=180,y=160)#自行设置最小置信度参数值，默认为0.7self.var2=tk.StringVar()self.var2.set('0.7')self.entry3=tk.Entry(self.window, show=None, width='3', font=('Arial', 16), textvariable=self.var2)self.entry3.place(x=180,y=220)#选择所需算法self.btnlist=tk.IntVar()self.radiobtn1=tk.Radiobutton(self.window, variable=self.btnlist, value=0, text='Apriori算法', font=('bold'), command=self.runApriori)self.radiobtn1.place(x=30,y=290)self.radiobtn2=tk.Radiobutton(self.window, variable=self.btnlist, value=1,text='FP-Growth算法', font=('bold'), command=self.runFPGrowth)self.radiobtn2.place(x=30,y=330)self.btnlist.set(0)#开始运行按钮
#        self.btn1=tk.Button(self.window, bg='green',fg='white', text='运行', font=('楷体', 12,'bold'), width=6, height=1, command=self.run)
#        self.btn1.place(x=80,y=360)#清空页面按钮self.btn2=tk.Button(self.window, bg='green',fg='white', text='清屏', font=('楷体', 12,'bold'), width=6, height=1)self.btn2.place(x=80,y=390)self.btn2.bind("<Button-1>",self.clear)#关闭页面按钮self.btn3=tk.Button(self.window, bg='green',fg='white', text='退出', font=('楷体', 12,'bold'), width=6, height=1)self.btn3.place(x=80,y=450)self.btn3.bind("<Button-1>",self.close)#主窗口循环显示self.window.mainloop()#清空所填内容   def clear(self,event):
#       连同导入文件一起删除的话，会影响操作的连贯性,故注释掉
#        self.entry1.delete(0,tk.END)
#        self.entry2.delete(0,tk.END)
#        self.entry3.delete(0,tk.END)self.text1.delete("1.0",tk.END)self.text2.delete("1.0",tk.END)#退出系统，对控制台清屏   def close(self,event):e=tk.messagebox.askokcancel('询问','确定退出系统吗？')if e==True:exit()self.window.destroy() def __del__(self):# 恢复sys.stdoutsys.stdout = sys.__stdout__sys.stderr = sys.__stderr__#从输入文本框中获取文本并返回数字列表def getDataSupport(self):  entry_num1 = float(self.var1.get())return entry_num1def getDataConfidence(self): entry_num2 =float(self.var2.get())return entry_num2def openfile(self):nameFile = filedialog.askopenfilename(title='打开文件', filetypes=[('csv', '*.csv'),('txt', '*.txt')])self.entry1.insert('insert', nameFile)def getnamefile(self):namefile=self.var0.get()return namefile#读取导入的文件并转化为列表def loadDataSet(self):nameFile=self.getnamefile()with open(nameFile,"r",encoding='utf-8') as myfile:data=myfile.read()self.text1.insert("0.0",data)self.text1.see("end")list_result=data.split("\n")# 以回车符\n分割成单独的行length=len(list_result)for i in range(length):list_result[i]=list_result[i].split(",") # csv文件中的元素是以逗号分隔的return list_resultdef runApriori(self):loadDataSet = self.loadDataSet()C1=self.createC1(loadDataSet)D = list(map(set,loadDataSet))minSupport = self.getDataSupport()L1, suppData0 = self.scanD(D,C1,minSupport)L,suppData = self.apriori(loadDataSet,minSupport)minConf = self.getDataConfidence()rules = self.generateRules(L,suppData,minConf)s='#######################Apriori算法##########################\n'self.text2.insert('insert',s)t1='\n频繁项集：\n'self.text2.insert('insert',t1)self.text2.insert('insert',L)t2='\n\n强关联规则：\n'self.text2.insert('insert',t2)for line in rules:r =str(line[0]) + '-->' + str(line[1]) + '置信度：' + str(line[2]) + '\n'self.text2.insert('insert',r)def runFPGrowth(self):dataSet = self.loadDataSet()frozenDataSet = fp.transfer2FrozenDataSet(dataSet)minSupport = self.getDataSupport()s='#######################FP_Growth算法########################\n'self.text2.insert('insert',s)t='\nFP树：\n'self.text2.insert('insert',t)fptree, headPointTable = fp.createFPTree(frozenDataSet, minSupport)fptree.disp()self.text2.insert('insert',fptree.display())frequentPatterns = {}prefix = set([])fp.mineFPTree(headPointTable, prefix, frequentPatterns, minSupport)t1='\n频繁项集：\n'self.text2.insert('insert',t1)t2=frequentPatternsself.text2.insert('insert',t2)minConf = self.getDataConfidence()rules = []fp.rulesGenerator(frequentPatterns, minConf, rules)t3='\n\n强关联规则：\n'self.text2.insert('insert',t3)for line in rules:r =str(line[0]) + '-->' + str(line[1]) + '置信度：' + str(line[2]) + '\n'self.text2.insert('insert',r)#创建集合C1，C1是大小为1的所有候选项集合def createC1(self,dataSet):C1 = []for transaction in dataSet:for item in transaction:if not [item] in C1:C1.append([item])      C1.sort()return list(map(frozenset,C1)) #对C1中每个项构建一个不变集合#扫描数据集，返回最频繁项集的支持度supportData                      def scanD(self,D, Ck, minSupport):ssCnt = {}for tid in D:for can in Ck:if can.issubset(tid):if  can not in ssCnt:ssCnt[can] = 1else:ssCnt[can] += 1
#        numItems = float(len(D))retList = []supportData = {}for key in ssCnt:
#            support = ssCnt[key] / numItems #计算所有项集支持度support = ssCnt[key]if support >= minSupport:retList.insert(0,key)supportData[key] = supportreturn retList, supportData#创建候选项集Ckdef aprioriGen(self,Lk, k):retList = []lenLk = len(Lk)for i in range(lenLk):#前k-2个项相同时，将两个集合合并for j in range(i + 1, lenLk):L1 = list(Lk[i])[:k - 2]L2 = list(Lk[j])[:k - 2]L1.sort()L2.sort()if L1 == L2:retList.append(Lk[i] | Lk[j])return retList#Apriori算法函数def apriori(self,dataSet, minSupport):minSupport = self.getDataSupport()C1 = self.createC1(dataSet)D = list(map(set, dataSet))L1, supportData = self.scanD(D, C1, minSupport)L = [L1]k = 2while (len(L[k - 2]) > 0):Ck = self.aprioriGen(L[k - 2], k)Lk, supK = self.scanD(D, Ck, minSupport)#扫描数据集，从Ck得到LksupportData.update(supK)L.append(Lk)k += 1return L, supportData#生成关联规则def generateRules(self,L, supportData, minConf): minConf = self.getDataConfidence()bigRuleList = []for i in range(1, len(L)):for freqSet in L[i]:H1 = [frozenset([item]) for item in freqSet]if (i > 1):self.rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)else:self.calcConf(freqSet, H1, supportData, bigRuleList, minConf)return bigRuleList #计算可信度值def calcConf(self,freqSet, H, supportData, brl, minConf):minConf = self.getDataConfidence()prunedH = []for conseq in H:conf = supportData[freqSet]/supportData[freqSet-conseq]if conf >= minConf:
#                print (freqSet-conseq,'-->',conseq,'conf:',conf)brl.append((freqSet-conseq, conseq, conf))prunedH.append(conseq)return prunedH#从最初的项集中生成更多的关联规则def rulesFromConseq(self,freqSet, H, supportData, brl, minConf):minConf = self.getDataConfidence()m = len(H[0])if (len(freqSet) > (m + 1)):Hmp1 = self.aprioriGen(H, m+1)Hmp1 = self.calcConf(freqSet, Hmp1, supportData, brl, minConf)if (len(Hmp1) > 1): self.rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)               
if __name__ == '__main__':GUI()

FP.py实现FP-Growth算法

# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 10:48:56 2019@author: 29493
"""
#import GUI
def transfer2FrozenDataSet(dataSet):frozenDataSet = {}for elem in dataSet:frozenDataSet[frozenset(elem)] = 1return frozenDataSetres1=[]
res2=[]
res3=[]class TreeNode:def __init__(self, nodeName, count, nodeParent):self.nodeName = nodeNameself.count = countself.nodeParent = nodeParentself.nextSimilarItem = Noneself.children = {}def increaseC(self, count):self.count += countdef disp(self, ind=1):res1.append(self.nodeName)res2.append(self.count)res3.append(ind)for child in self.children.values():child.disp(ind + 1)   def display(self):s=''for i in range(0,len(res1)):s+='   ' * res3[i]+res1[i]+' '+str(res2[i])+'\n'return sdef createFPTree(frozenDataSet, minSupport):#scan dataset at the first time, filter out items which are less than minSupportheadPointTable = {}for items in frozenDataSet:for item in items:headPointTable[item] = headPointTable.get(item, 0) + frozenDataSet[items]headPointTable = {k:v for k,v in headPointTable.items() if v >= minSupport}frequentItems = set(headPointTable.keys())if len(frequentItems) == 0: return None, Nonefor k in headPointTable:headPointTable[k] = [headPointTable[k], None]fptree = TreeNode("null", 1, None)#scan dataset at the second time, filter out items for each recordfor items,count in frozenDataSet.items():frequentItemsInRecord = {}for item in items:if item in frequentItems:frequentItemsInRecord[item] = headPointTable[item][0]if len(frequentItemsInRecord) > 0:orderedFrequentItems = [v[0] for v in sorted(frequentItemsInRecord.items(), key=lambda v:v[1], reverse = True)]updateFPTree(fptree, orderedFrequentItems, headPointTable, count)return fptree, headPointTabledef updateFPTree(fptree, orderedFrequentItems, headPointTable, count):#handle the first itemif orderedFrequentItems[0] in fptree.children:fptree.children[orderedFrequentItems[0]].increaseC(count)else:fptree.children[orderedFrequentItems[0]] = TreeNode(orderedFrequentItems[0], count, fptree)#update headPointTableif headPointTable[orderedFrequentItems[0]][1] == None:headPointTable[orderedFrequentItems[0]][1] = fptree.children[orderedFrequentItems[0]]else:updateHeadPointTable(headPointTable[orderedFrequentItems[0]][1], fptree.children[orderedFrequentItems[0]])#handle other items except the first itemif(len(orderedFrequentItems) > 1):updateFPTree(fptree.children[orderedFrequentItems[0]], orderedFrequentItems[1::], headPointTable, count)def updateHeadPointTable(headPointBeginNode, targetNode):while(headPointBeginNode.nextSimilarItem != None):headPointBeginNode = headPointBeginNode.nextSimilarItemheadPointBeginNode.nextSimilarItem = targetNodedef mineFPTree(headPointTable, prefix, frequentPatterns, minSupport):#for each item in headPointTable, find conditional prefix path, create conditional fptree, then iterate until there is only one element in conditional fptreeheadPointItems = [v[0] for v in sorted(headPointTable.items(), key = lambda v:v[1][0])]if(len(headPointItems) == 0): returnfor headPointItem in headPointItems:newPrefix = prefix.copy()newPrefix.add(headPointItem)support = headPointTable[headPointItem][0]frequentPatterns[frozenset(newPrefix)] = supportprefixPath = getPrefixPath(headPointTable, headPointItem)if(prefixPath != {}):conditionalFPtree, conditionalHeadPointTable = createFPTree(prefixPath, minSupport)if conditionalHeadPointTable != None:mineFPTree(conditionalHeadPointTable, newPrefix, frequentPatterns, minSupport)def getPrefixPath(headPointTable, headPointItem):prefixPath = {}beginNode = headPointTable[headPointItem][1]prefixs = ascendTree(beginNode)if((prefixs != [])):prefixPath[frozenset(prefixs)] = beginNode.countwhile(beginNode.nextSimilarItem != None):beginNode = beginNode.nextSimilarItemprefixs = ascendTree(beginNode)if (prefixs != []):prefixPath[frozenset(prefixs)] = beginNode.countreturn prefixPathdef ascendTree(treeNode):prefixs = []while((treeNode.nodeParent != None) and (treeNode.nodeParent.nodeName != 'null')):treeNode = treeNode.nodeParentprefixs.append(treeNode.nodeName)return prefixsdef rulesGenerator(frequentPatterns, minConf, rules):for frequentset in frequentPatterns:if(len(frequentset) > 1):getRules(frequentset,frequentset, rules, frequentPatterns, minConf)def removeStr(set, str):tempSet = []for elem in set:if(elem != str):tempSet.append(elem)tempFrozenSet = frozenset(tempSet)return tempFrozenSetdef getRules(frequentset,currentset, rules, frequentPatterns, minConf):for frequentElem in currentset:subSet = removeStr(currentset, frequentElem)confidence = frequentPatterns[frequentset] / frequentPatterns[subSet]if (confidence >= minConf):flag = Falsefor rule in rules:if(rule[0] == subSet and rule[1] == frequentset - subSet):flag = Trueif(flag == False):rules.append((subSet, frequentset - subSet, confidence))if(len(subSet) >= 2):getRules(frequentset, subSet, rules, frequentPatterns, minConf)

在引入FP.py的时候，现在Python\Lib\site-packages下创建一个mylib文件夹，然后再把该文件复制到mylib的文件中去，就可以直接引用了。