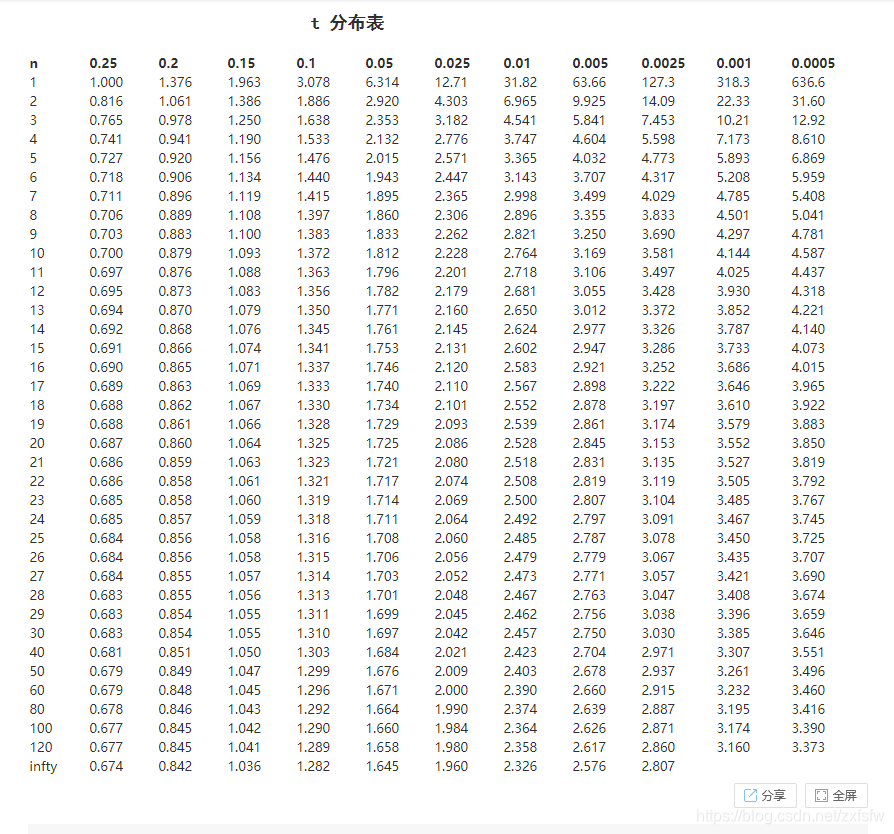
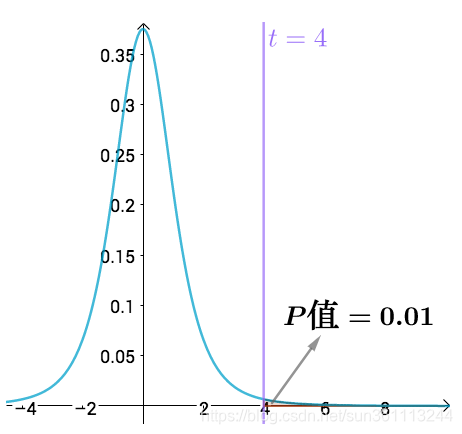
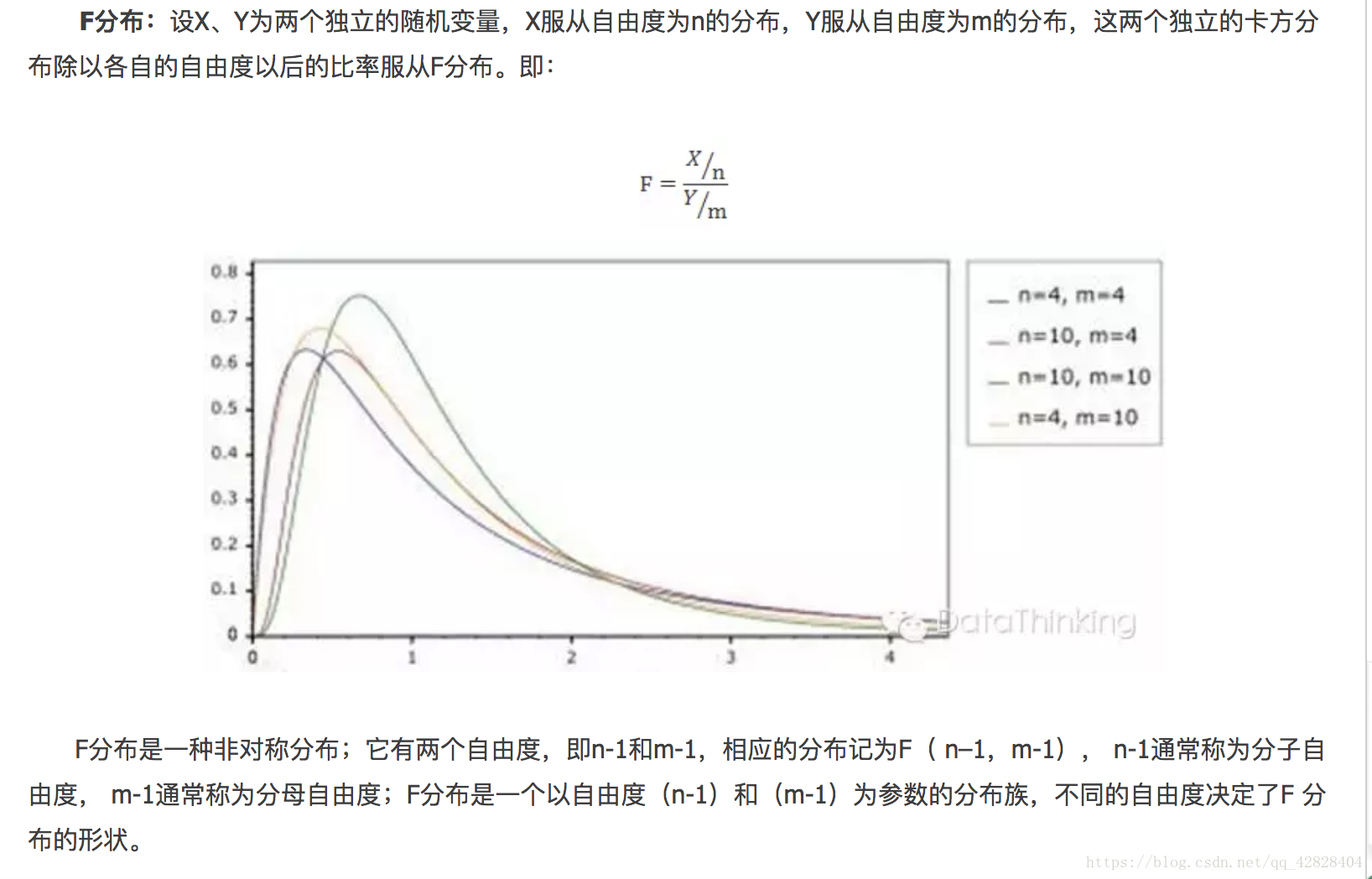
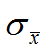1 关联规则产生的原因:购物篮问题
关联规则最初是为了解决购物篮问题而产生。上世纪九十年代,美国的沃尔玛超市发现,啤酒和尿布这两种完全不着边际的商品竟然有很高的概率一起被购买。
在一段时间之后,他终于分析出了原因:
在美国有婴儿的家庭中,一般是母亲在家中照看婴儿,年轻的父亲去超市买尿布。父亲在购买尿布的同时,往往会顺便为自己购买啤酒。所以尿布和啤酒一起出现的概率就很高。
2 关联规则
关联规则是形如X→Y的蕴涵式,其中, X和Y分别称为关联规则的先导(left-hand-side, LHS)和后继(right-hand-side, RHS) 。
3 几个重要的概念
在说概念之前,我们看一下我们这一小节涉及的数据集:

3.1 项
每一小件商品(如A、B、C、D),称之为一个项
3.2 记录
每一组商品的组合(如ABCD),称之为一条记录
3.3 项(目)集
由项组成的集合(不一定是记录里面有的组合),如{A,B,C},{A,B,D}都是项集
3.4 K项集
项集中的元素个数为K,如{A,B,C}就是一个三项集
3.5 事务集
所有的记录构成的集合称之为事务集
在上图中,{ABCD,ABCE,BDEF,BCDE,ACDF,ABC,ABE}称之为一个事务集
3.6 支持度
 ’
’
简单理解就是频率。而在数据量大的时候,频率又可以近似为概率
Sup(X)可以理解为某个项集出现的概率

以数据集
为例 sup({A,C})=4/7 (一共有7组数据,{A,C}同时出现的有4组)
3.7 置信度
简单理解就是条件概率(XY同时出现的概率/X出现的概率)
如果X={A},Y={C},那么Con(X->Y)=
换言之,置信度等于X出现的基础上,出现Y的概率。这样想也是0.8
3.8 最小支持度
人为规定的一个支持度(后面会说明)
3.9 最小置信度
人为规定的一个置信度(后面会说明)
3.10 提升度
![]()
理解为B在A发生的基础上再发生的概率,和B单独发生的概率的比值
如果提升度大于1,表示A的出现对于B的概率有推动作用。
3.11 频繁K项集
支持度比最小支持度大的K项集

比如我们最小支持度为0.5,sup({A,C})=4/7 >0.5 所以{A,C}是一个频繁2项集
3.12 候选K项集
用来生成频繁K项集的项集(后面会说明)
这个值不等价于所有K项集(后面会说明)
4 关联规则定理
定理1:如果X是一个频繁K项集,那么它的所有子集也是
X的子集出现的数量肯定大于等于X出现的数量(子集可能出现在非X的K项集里面),所以X子集的支持度肯定大于X的支持度。那么既然X都是频繁K项集了,它的子集更是。
定理2:如果X的子集不是k-1项频繁,那么它一定不是频繁K项集
和定理1同样的说明方法,X的子集的支持度肯定比X要大。那么既然子集都没有大于最小支持度,那么X更没有。
5 关联准则主要步骤(Apriori算法)
- 令K=1,计算每个商品的支持度,并筛选出频繁1项集
- 从K=2开始,根据K-1项的频繁K-1项集,生成K项候选集,并进行预剪枝
- 从候选K项集生成频繁K项集
重复2和3 直到无法筛选出满足最小支持度的项集
4. 将前面循环获得的最终频繁K项集依次取出。同时计算取出的这个K项集的所有真子集,以排列组合的方式形成关联规则,并计算关联规则的置信度和提升度,将符合要求的关联规则提出
算法结束
6 关联规则案例研究
我们令最小支持度是0.3(2.1/7)

第一步: 令K=1 计算所有单个商品的支持度,筛选出频繁1项集
K=2 时的第二步:根据k-1(即1)的频繁1项集生成候选二项集,并进行预剪枝。
这一步得到的是所有的二项组合(并没有做划去{A,D}这些的操作)
(这一步还没有预剪枝)
K=2时的第三步 从候选K项集生成频繁K项集
将上一步得到的候选二项集中支持度小于最小支持度的去掉(即去掉{A,D}这一类项集)
K=3 时的第二步:根据k-1(即2)的频繁2项集生成候选三项集,并进行预剪枝。
K=3时的第三步 从候选K项集生成频繁K项集
第四步
细心的话会发现,这里没有{A,C}和{A,B}的组合,因为这两个的组合和{C}和{B}之间的组合没有区别
7 算法缺点
- 时间复杂度大(每次计算一个K项集的支持度时,都需要扫描一遍事务集)
- 频繁项目集长度变大的情况下,运算时间显著增加
- 采用唯一支持度,没有考虑各个属性的重要程度
8 总结
如果一个规则 X->Y 是一个最小支持度s,最小置信度c的关联规则,那么它需要满足:
1) X ∪ Y 的 支持度大于s
2)X->Y的置信度大于c
参考资料:通俗易懂讲算法-关联规则_哔哩哔哩_bilibili