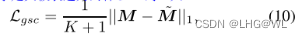周志华 A Brief Introduction to Weakly Supervised Learning 2018
引言
在机器学习领域,学习任务可以划分为监督学习、非监督学习。通常,两者都需要从包含大量训练样本的训练数据集中学习预测模型。
监督学习的训练数据包括,数据对象向量、任务标签;
非监督学习训练数据包括,数据对象向量,但无标签。
分类问题和回归问题是监督学习的代表,聚类学习是非监督学习的代表。
尽管当前监督学习技术已取得巨大成功,但由于数据标注过程成本太高,很多任务很难获得真知标签。而无监督学习由于学习过程困难,以及目前预训练模型发展完善。因此,机器学习技术能够在弱监督状态下工作。
弱监督学习
弱监督学习分为三种类型,不完全监督(Incomplete supervision),不确切监督(Inexact supervision),不精确监督(Inaccurate supervision)。
不完全监督是指,训练数据中只有部分数据给了标签,有一些数据是无标签的。
不确切监督是指,训练数据只给出了粗粒度标签。给出一些数据整体的标签,但不知道每个示例的标签。
不精确监督是指,给出的标签不总是正确的。
在实际操作中,它们经常同时发生。
比如,在图像分类任务中,训练数据的Groud-Truth标签由人类注释者给出; 虽然很容易从互联网上获取大量图像,而由于人工成本,只能注释一小部分图像。(不完全监督)
在重要目标检测中,我们常常仅有图片级标签,而没有对象级标签。(不确切监督)
在众包数据分析中,当图像标记者粗心或者疲倦时,或者有些图片很难去分类时,这将会导致一些标签被标记错误。(不精确监督)
解决方案
为了解决不完全监督,主要考虑两种技术:主动学习和半监督学习。
为了解决不确切监督,可以考虑多示例学习。
为了解决不精确监督,可以考虑带噪学习。
不完全监督
主动学习(active learning):输入标记过的数据(x, y)和没有标记过的数据(x),输出是Y或者N(二分类问题);在未标记数据中,主动学习尝试选择最有价值的未标记示例进行查询。最有价值指的是信息性和代表性。主动学习的目标是最小化查询的数量。

半监督学习(Semi-supervised learning):根据positive和negative 与 未被标记的数据分布,来判断未标记数据的标签。
上图的例子。已知一个数据是positive,另一个数据是negative,在两个数据点正中间有一个test data。观察未被标注的数据分布(右边部分的灰点),这时可以较肯定的认为test data是positive。
不确切监督
多实例学习(Multi-instance learning):训练数据中每个数据看作一个包(Bag),每个包由多个实例(instance)构成,每个包由一个可见的标签,假设包大小为88,如果我们用size为22的图片包生成器去取示例,那么可以得到16个实例。
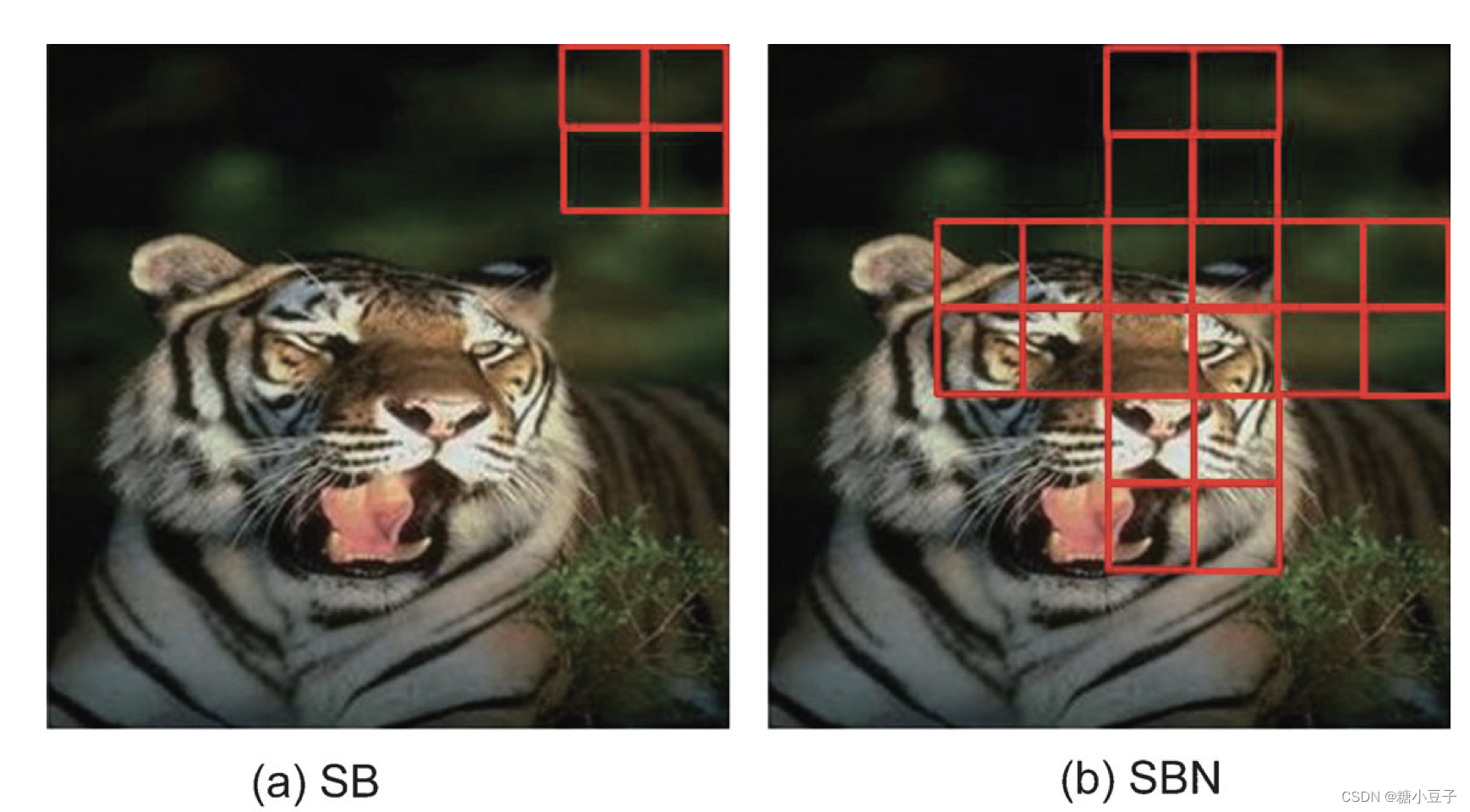
多实例学习假设每个正包必须存在至少一个关键实例。多实例学习的过程就是通过模型对包及其包含的多个实例进行分析预测得出包的标签。
不精确监督
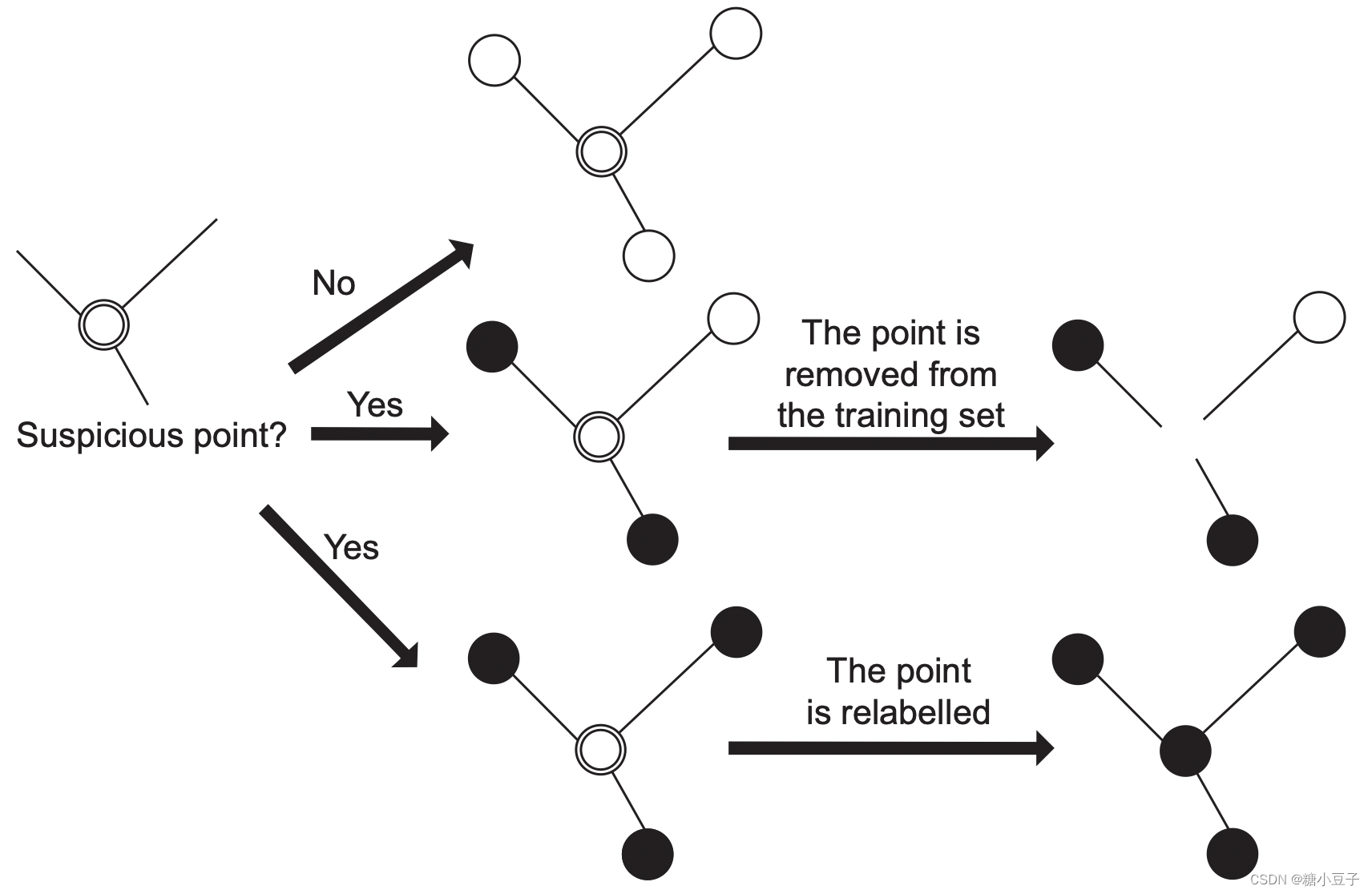
带噪学习(Learning with label noise):识别潜在的误分类样本,然后尝试进行修正。例如,用数据编辑的方法构建关系相邻表。判断一个表是否为可疑点。如果这个点和相邻的点不一样,该点是可疑的,将被删除或被重新标记。