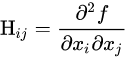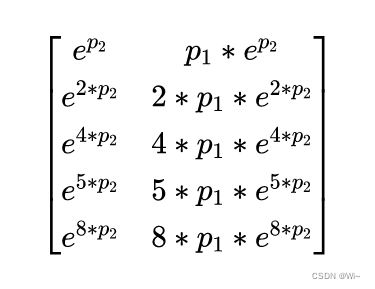supervised pca很简单粗暴，计算$X$的每一个纬度和$Y$的相关性，取一个阈值，丢掉一些纬度，然后用普通的pca降维。

---

如何计算两个随机变量的相关性/相似性？
两个随机变量$X,Y$，有一个函数$\varphi$，可以把一维随机变量映射到高维空间，映射后两个向量均值的距离可以表示两个随机变量的相关性。
$$\begin{array}{rl}& |\sum _{i=1}^n\varphi (x_i)-\sum _{j=1}^m\varphi (y_i){|}^2\\ =& (\frac{1}{n}\sum _i\varphi (x_i)-\frac{1}{m}\sum _j\varphi (y_j){)}^T(\frac{1}{n}\sum _i\varphi (x_i)-\frac{1}{m}\sum _j\varphi (y_j))\\ =& \frac{1}{n^2}\sum _{i,j}K(x_i,x_j)+\frac{1}{m^2}\sum _{ij}K(y_i,y_j)-\frac{2}{mn}\sum _{i,j}K(x_i,x_j)\end{array}$$
$K$可以取RBF，$K(x_i,x_j)=e^{-\frac{|x_i-x_j{|}^2}{r}}$
这就是MMD,Maximun Mean distance.

---

判断两个随机变量的相关性$|P(x,y)-P(x)P(y){|}^2$，这个叫做HSIC

---

dataset $X_{d\ast n},Y_{q\ast n}$, { ( x i , y i ) } i = 1 n \{(x_i,y_i)\}_{i=1}^n {(xi​,yi​)}i=1n​，$x_i\in R^d,y_i\in R^q$.
$K$ is an n by n matrix as the result of applying a kernel K on data set X.
$B$ is an n by n matrix as the result of apply a kernel function B on data set Y.
$Tr(KHBH)$ is a measure of dependence.

• Goal: find a linear transformation U, such that $U^{T}X$ has maximum dependence to Y.
• make a linear kernel on $U^{T}X$
• ${\max }_U\frac{1}{(n-1{)}^2}Tr(X^{T}U{U}^{T}XHBH)$
• ${\max }_{U}Tr(U^{T}XHBH{X}^{T}U)$ add a constraint $U^{T}U=I$
• U will be the top p eignenvectors of $XHBH{X}^T$
  $XH$~$(X-\bar{X})$
  
  
  kernel supervised pca

待续，不是很理解