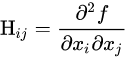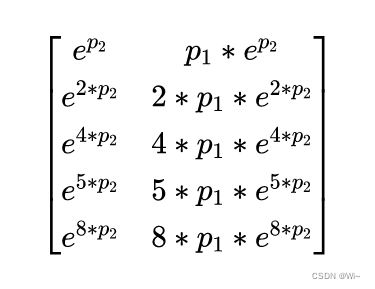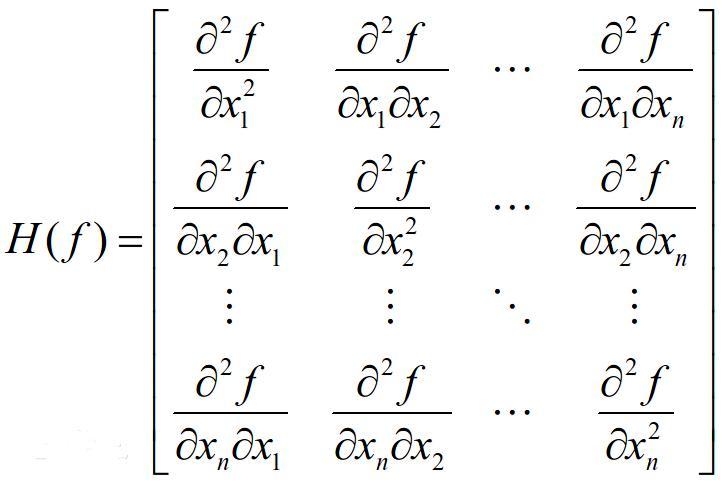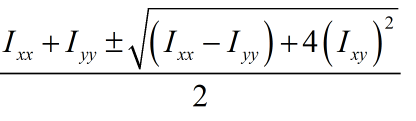O(n) o(n)
order:阶,多次式阶,x^2+x+1 阶2
f(x)=O(g(x)):存在x0、M,使得x>=x0时,f(x)<=Mg(x)
2x^2 = O(x^2),M=2,x0任意
x^2+x+1 = O(x^2),M=2,x0=10
f(x)=o(g(x)):对于任意的ε,存在x0,使x>=x0时,f(x)<=εg(x)
x=o(x^2)
x^2+x+1 = o(x^3)
表示f(x)的阶比g(x)小
维基百科:
大O符号(英语:Big O notation),又称为渐进符号,是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。

方向导数
在函数定义域的内点,对某一方向求导得到的导数。一般为二元函数和三元函数的方向导数,方向导数可分为沿直线方向和沿曲线方向的方向导数。

可微
在微积分学中,可微函数是指那些在定义域中所有点都存在导数的函数。可微函数的图像在定义域内的每一点上必存在非垂直切线。因此,可微函数的图像是相对光滑的,没有间断点、尖点或任何有垂直切线的点。
一般来说,若X0是函数f定义域上的一点,且f′(X0)有定义,则称f在X0点可微。这就是说f的图像在(X0, f(X0))点有非垂直切线,且该点不是间断点、尖点。
可微分 → 在x0处连续 & 偏导存在
偏导存在 + 偏导连续 → 可微
梯度

链式法则




在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。偏导数在向量分析和微分几何中是很有用的。
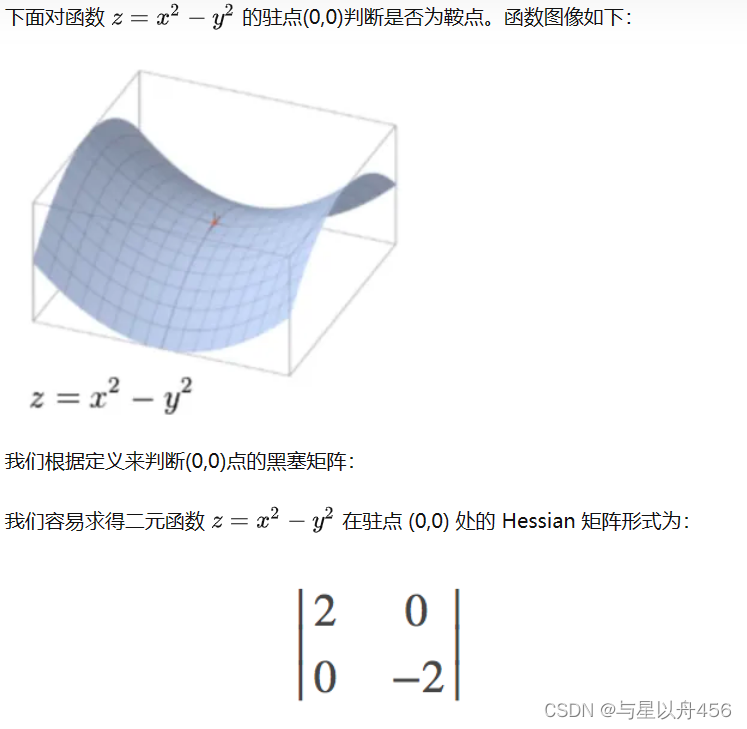
Hessian矩阵
黑塞矩阵(Hessian Matrix),又译作海森矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。

二元函数的黑塞矩阵

Hessian矩阵判断极值点
- Hessian矩阵正定时,函数在该点处是极小值;
- Hessian矩阵负定时,函数在该点处是极大值;
- Hessian矩阵不定时,该点不是函数极值点;
- Hessian矩阵为半正定矩阵或半负定矩阵时,该点为“可疑”极值点,尚需要利用其他方法来判定。
拉格朗日乘数法
在数学最优问题中,拉格朗日乘数法(以数学家约瑟夫·路易斯·拉格朗日命名)是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。
这种方法将一个有n个变量与k个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方程的梯度(gradient)的线性组合里每个向量的系数。
此方法的证明牵涉到偏微分,全微分或链法,从而找到能让设出的隐函数的微分为零的未知数的值。