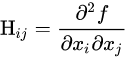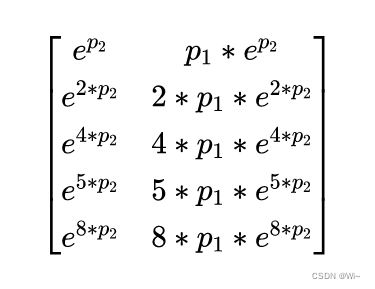1. 自监督学习的概念

在机器学习中，最常见的是监督学习（Supervised learning）。假设模型的输入是$x$，输出是$y$，我们如何使模型输出我们期望的$y$呢？我们得拥有已标注的（label）的数据，例如图片识别，我们得有一堆的图片，并且这些图片被标注了是什么。然后通过这些已标注的数据对模型进行训练，使模型的输出$y$尽可能地接近标签$y^{\prime }$，这是监督学习。那么什么是自监督学习呢？假设我们拥有一堆的数据，但是没有标注，我们想办法将这堆数据$x$分成两个部分，一部分作为模型的输入$x^{\prime }$，一部分作为模型的标签$x^{\prime \prime }$。然后对模型进行训练，使模型地输出$y$尽可能地接近标签$x^{\prime \prime }$。注意这里$x^{\prime \prime }$不是人标注的，而是数据里本来就有的。这说起来有点抽象，但是通过BERT这个例子就很容易明白了。

2. BERT概述

BERT的全称是Bidirectional Encoder Representation from Transformers，即双向Transformer的Encoder。因此BERT的网络架构和Transformer的Encoder是一样的，关于Transformer的细节请看上一节。因此BERT的任务就是输入一个序列，然后输出一个序列，输出序列和输入序列的长度是一样的。通过Transformer中的自注意力机制，BERT具有考虑序列全局的能力。由于BERT一般用于自然语言处理，所以BERT的输入一般使一排文字，然后输出一组向量，向量的个数和文字的个数是一样的。

3. BERT的训练

所谓自监督学习，和监督学习不同的地方就在于训练。BERT的训练方式有两种：Masked Language Model和Next Sentence Prediction。

3.1 Masked Language Model

Masked Language Model的工作机制如下图所示，类似于让BERT做完形填空。在训练过程中，随机盖掉句子中的一些字，这些被盖掉的字要么替换成一个特殊符号“MASK”，要么随机替换成其他字。然后将替换后的句子当成BERT的输入，被盖掉的字对应的输出向量通过一个Linear层和softmax操作之后输出一个概率分布。前面讲transformer的时候，讲到了这个概率分布向量的长度和字典的长度是一样的，每个字都有一个对应的概率，概率最大的字就是最后的预测结果。在训练过程中，要使预测输出的字和被盖掉的字尽可能一致。这其实就是一个分类问题，类别的数目和字典的大小一样，损失函数是交叉熵。通过这种简单的方式就实现了自监督学习，它不需要我们去人工标注数据，它的标签来自于数据本身，这是非常巧妙的。

3.2 Next Sentence Prediction

Next Sentence Prediction的工作机制如下图所示。在Next Sentence Prediction的训练任务中，BERT的输入是两个句子加上两个特别的符号“CLS”，“SEP”。其中“CLS”是一个开始符号，“SEP”将两个句子隔开。Next Sentence Prediction的任务是要预测这两个句子是否是相接的，“CLS”输出的向量通过Linear层后输出“yes”和“no”，“yes”表示两个句子是前后相接的，“no”则相反。训练数据的正例是正常的一篇文章中上下连贯的两句话，负例是将正常相接的下一句话随即替换成另外一句话。但是研究表明，这种训练任务对于BERT的训练用处不大。因此BERT的训练主要还是依赖于Masked Language Model。

4. BERT的应用

BERT在自然语言处理领域基本上都可以用上，其应用机制如下图所示，分为预训练（Pre-train） 和微调（Fine-tune） 两个部分。
预训练（Pre-train） 就是指上面所说的Masked Language Model和Next Sentence Prediction两个自监督训练任务。这部分工作实际上由一些搞深度学习的大户做好了，比如google、讯飞等，并不需要我们自己训练，我们只需要将人家训练好的BERT拿来用就行了。
微调（Fine-tune） 是指根据我们的下游任务（如机器翻译、智能问答、文本标注等），再利用下游任务的少量标注数据对下游任务的参数进行微调即可。

下面以“基于抽取的智能问答（Extraction-based Question Answering）”为例说明BERT的应用机制。“基于抽取的智能问答”类似于阅读理解，让机器读一段文字，然后提出几个问题，机器从阅读到的文字中抽取答案。对于该任务，模型的输入就是文章和问题，输出是两个整数值“$s$”和“$e$”。“$s$”代表答案在文章中的起始位置，“$e$”代表答案在文章中的结束位置。例如下图中第一个问题的答案是“gravity”，而“gravity”位于文章的第17个字符（不含标点），因此模型的输出“$s=17$”，“$e=17$”。同理，第三个问题的答案是“within a cloud”，而它们位于第77-79个字符，因此模型的输出“$s=77$”，“$e=79$”。

处理上述这个问题的做法如下图所示，模型的输入是问题和文章，问题和文章通过符号“SEP”隔开。然后随机初始化两个向量（图中的橘黄色向量和蓝色向量），向量的长度和BERT输出向量的长度一样，然后将这两个向量分别去和文章输出的向量做点积，然后通过Softmax输出概率分布，概率最大的分别是答案的起始位置和结束位置。这个任务中训练的参数只有随机初始化的两个向量，BERT中的参数都不需要训练的。

可以看出利用BERT的预训练，做下游任务时就很简单了，训练的参数也非常少，而且实践证明这样做的效果是非常好的，超过了传统的一些做法。这就是BERT的魅力所在。