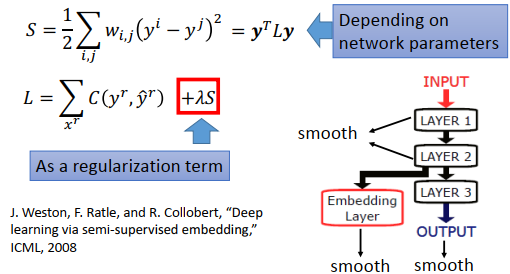
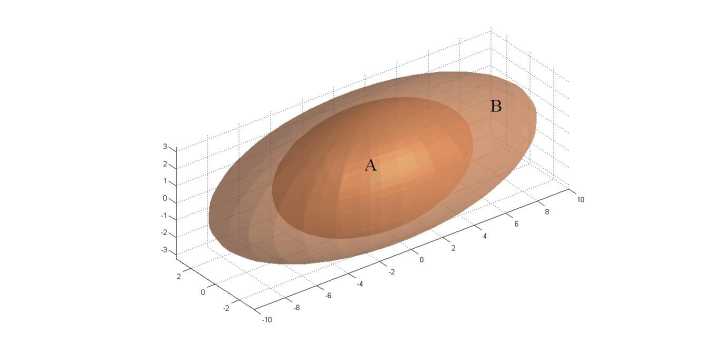
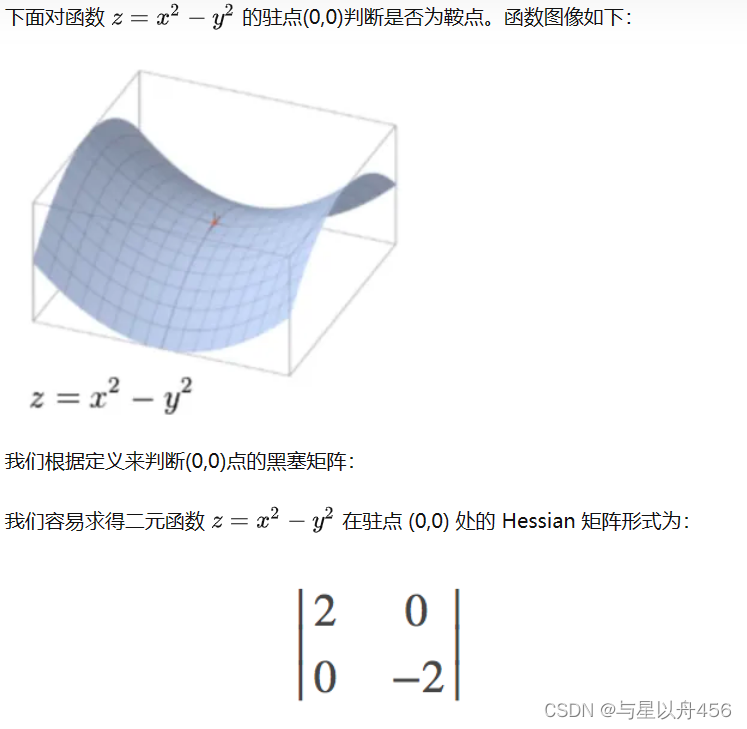
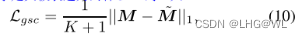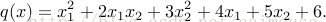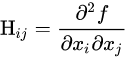在CV中,以数据与神经网络为基础,我们通常以supervised的方式与unsupervised的方式来进行网络的训练,这些行为的目的都是为了想要使学到的网络能够具有较好的特征表示能力,以进行如分类、目标检测、语义分割等。这两种方式的主要异同在于数据是否有无label。
Supervised:
以简单的分类任务为例:
现有不同的猫的数据集:n张,标签均以1表示;不同的狗的数据集:n张,标签均以0表示;
以supervised的方式进行训练,将这些样例输入网络模型中,通过数据与标签构建损失,以进行梯度反传更新,最终目标使得同一类的特征表示尽可能相同。
以上方法可行的主要原因是:在相同的类标签下,这些样例具有相似的特征分布。
然而现实生活中,往往许多领域中的数据缺乏标注,如医疗诊断图像数据,而我们如何合理有效的利用这些数据,从这些数据中挖掘分析有用信息,以辅助我们的生活,为我们生活提供便利则显得格外重要。
Self-supervised
self-supervised中,往往是以contrastive learning的方式,以构建pretext tasks的形式来生成pseudo label进行模型训练。
主要是采用数据增强的方式,来构建正负样例对,目的是最大化正例样例对间的相似性,最小化负例样例对间的相似性。
缺陷:在上述方法中,均只考虑了所对应正例为一类,批量中的其余所有剩余样例均为该样例的负例,而忽略了这些样例中其他样例可能包含与正例同属于同一类的其他样例,不应该把它们都统归为负样本。
此处便涉及到了统计学的问题,只要在这批数据中,我的负样例足够多,反言之即正样例就相对很少,则这个别的正例被归为负样例所造成的影响会非常小。统计上将它们归为负样例是一个可取的问题,所以contrastive learning(SimCLR,MoCO)中对负样例的数据要求是很大的,因为负样例越多,被当成负样例的正样例占比就越少,对网络的影响也会越少,使得最终学习到的网络性能就越好。