受限玻尔兹曼机RBM简述与Python实现

生成式模型

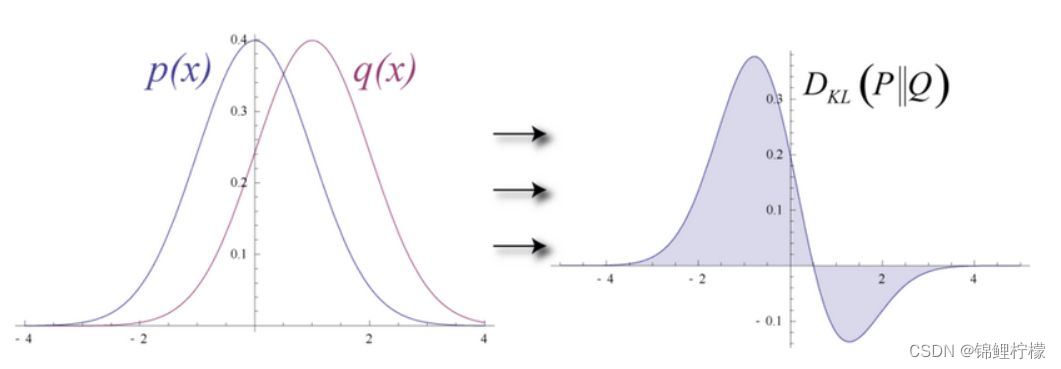
生成式模型的理念大同小异，几乎都是用一个模型产生概率分布来拟合原始的数据分布情况，计算两个概率分布的差异使用KL散度，优化概率模型的方法是最小化对数似然，可以用EM算法或梯度优化算法。
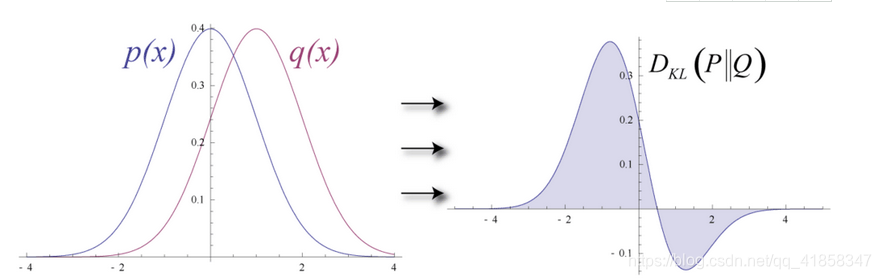
在这里插入图片描述
今天表现比较好的生成模型有VAE变分自编码器，GAN生成对抗网络和PixelRNN以及Seq2Seq等。而RBM则比它们要早很多，可以说是祖师爷级别的模型。

受限玻尔兹曼机

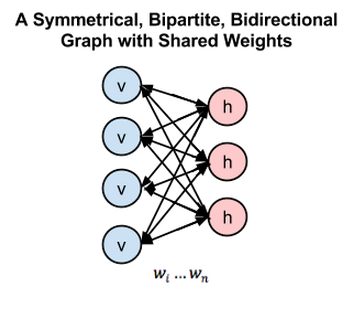
RBM模型是一种很早被提出的基于能量和概率的生成式模型，它拥有一个显层和一个隐层，层上有偏置，两层之前有一个权值矩阵W，只是看起来的话结构和单层神经网络并无区别。但是我们会定义这些神经元拥有“开启”或“关闭”的二值状态，为什么这样定义下面再说。
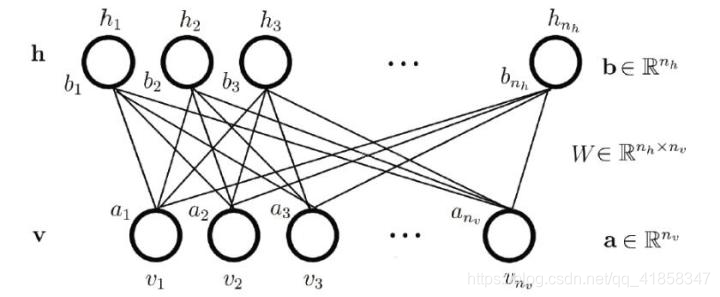
在这里插入图片描述
我们希望用一个概率分布来拟合数据分布，这个概率分布的定义如下。

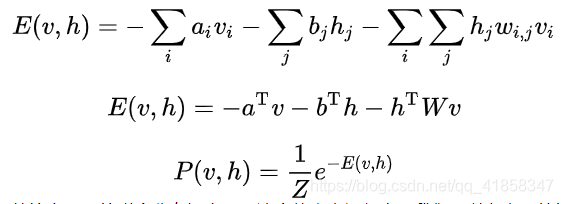
在这里插入图片描述
其中我们先给出能量函数，再用能量函数的指数分布作为显层向量v和隐层向量h的联合分布概率密度。如果你和我一样，大学里学过统计物理的知识就会发现，这个形式就是玻尔兹曼分布，在描述粒子的分布时非常有用。
同样的，描述粒子分布的方法用在数据科学上也有不错的效果，实践也证明了这个概率密度往往能比较好的拟合数据。
但是仍然存在一个问题，hidden values是人为定义出来的；我们的训练数据只有显层输入v，这时我们也有方法推进训练，就是用贝叶斯公式，把上面的联合概率分布转为条件概率分布，如下。
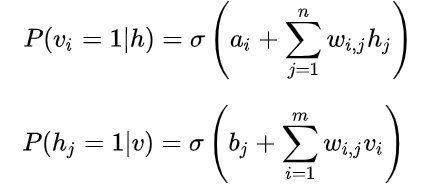
在这里插入图片描述
形式就是前馈网络里的sigmoid激活加线性变换，得到的向量就是神经元是否被激活的概率。这时如果我们拿到显层输入，就能计算出隐层的概率分布。
也就是对给定的权值W和偏置bias_hidden、bias_visible，以及输入向量v，就能计算出h的概率分布。这就引申出了一种独特的训练方法，具体的推导可以看CD-k算法推导.

训练

总之更新公式是
$\frac{\partial lnL_\theta }{\partial w_{j,i} }=P\left ( h_j=1\mid \mathbf{v} \right )v_i-\sum_{\mathbf{v}}P\left ( \mathbf{v} \right )P\left ( h_j=1\mid \mathbf{v} \right )v_i$
$\frac{\partial lnL_\theta }{\partial a_i }=v_i-\sum_{\mathbf{v}}P\left ( \mathbf{v} \right )v_i$
$\frac{\partial lnL_\theta }{\partial b_j }=P\left ( h_j=1\mid \mathbf{v} \right )-\sum_{\mathbf{v}}P\left ( \mathbf{v} \right )P\left ( h_j=1\mid \mathbf{v} \right )$
CD-k算法就是用采样来代替上面的求和期望(因为每个神经元都有0-1状态，状态空间有2^n那么多，直接计算期望不现实。
首先，我们把训练数据的v0向量放入网络，用上面的公式计算出条件概率p(h0|v0)，然后我们用这个概率进行采样，得到一组0-1的二值化向量，描述隐层神经元的开闭。然后再用这个h0和上面的公式计算p(v1|h0)，再用这个v的条件概率采样，就得到一个新的v向量，我们称它为重建向量。这个过程就称为“吉布斯采样”。这个采样过程也可以重复多次，也就是k次吉布斯采样。然后我们对比原向量和重建向量的差异，就能用它来更新梯度。更新方法是梯度上升，对比发散度CD = dW = v0.p(h0|v0)-v1.p(h1|v1)。
算法流程如下
在这里插入图片描述
到此为之模型的细节已经很清晰了，模型有一个W矩阵，b_hidden和b_visible向量作为参数。训练时，使用CD-k算法接收样本并更新参数，使用梯度上升法。使用时，模型可以接收任意的v输入，通过计算得到隐层h，再重构生成新的数据v1，这个v1一般会符合训练数据分布，也就是会和训练数据很像。
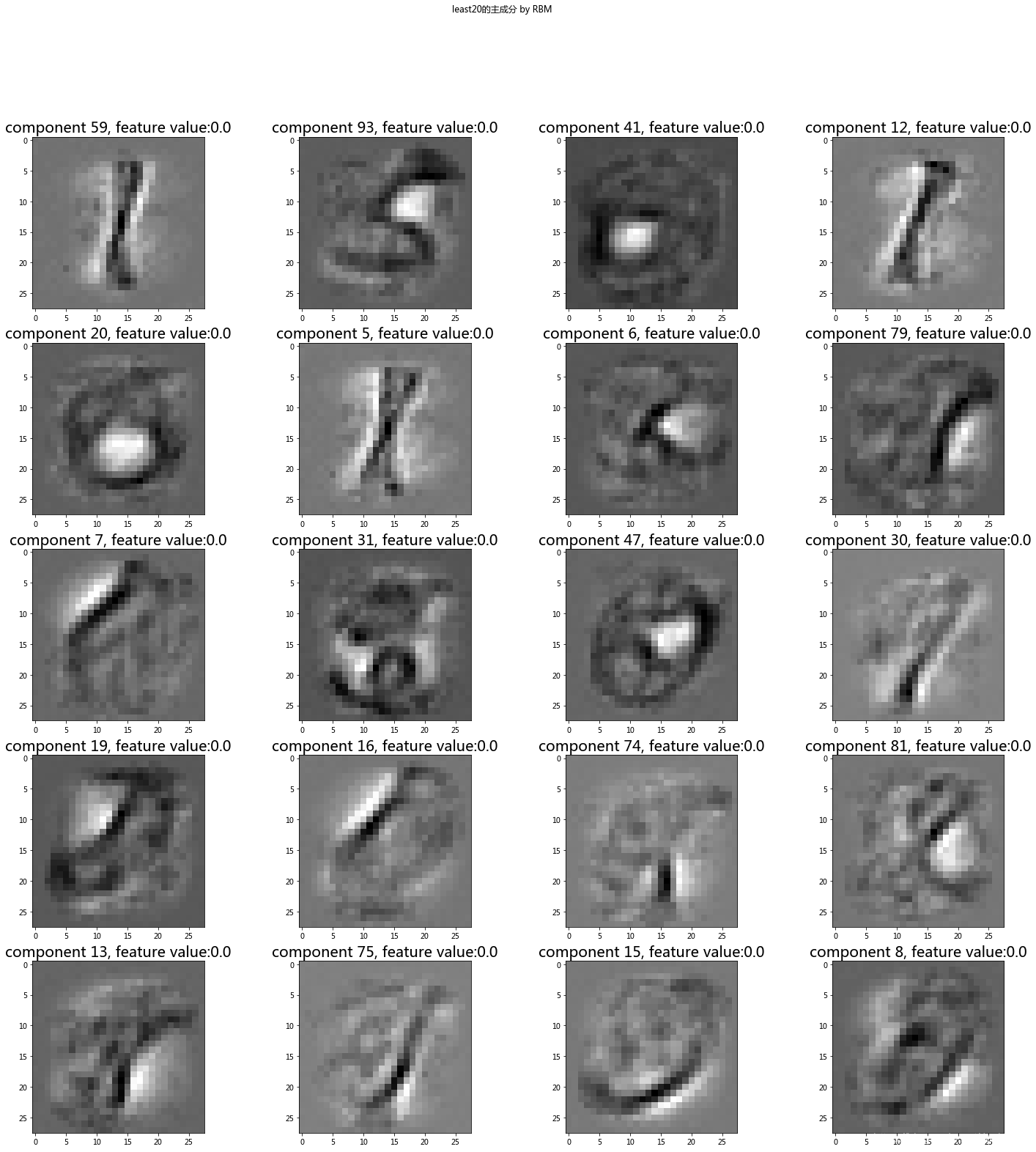
此外RBM的隐层就是从显层提取出的更深层的特征，RBM也是一个常用的特征提取和降维手段。

Python实现

我们用最简单的语言Python来做一下实现，我们做一个784-500的RBM来压缩MNIST数据集的特征。首先导入数据

import matplotlib.pylab as plt
import numpy as np
import random
import matplotlib.pyplot as pltimport tensorflow as tf
(x_train_origin,t_train_origin),(x_test_origin,t_test_origin) = tf.keras.datasets.mnist.load_data()
X_train = x_train_origin/255.0
X_test = x_test_origin/255.0
m,h,w = x_train_origin.shape
X_train = X_train.reshape((m,1,h,w))
data = X_train[:5000].reshape(5000,784)

然后设计一个RBM类用来训练

class RBM:'''设计一个专用于MNIST生成的RBM模型'''def __init__(self):self.nv = 784self.nh = 500self.lr = 0.1self.W = np.random.randn(self.nh,self.nv)*0.1self.bv = np.zeros(self.nv)self.bh = np.zeros(self.nh)def sigmoid(self,z):return 1.0/(1.0+np.exp(-z))def forword(self,inpt):z = np.dot(inpt,self.W.T) + self.bhreturn self.sigmoid(z)def backward(self,inpt):z = np.dot(inpt,self.W) + self.bvreturn self.sigmoid(z) def train_loader(self, X_train):np.random.shuffle(X_train)self.batches = []for i in range(0,len(X_train),self.batch_sz):self.batches.append(X_train[i:i+self.batch_sz])self.indice = 0def get_batch(self):if self.indice>=len(self.batches):return Noneself.indice += 1return np.array(self.batches[self.indice-1])def fit(self, X_train, epochs=50, batch_sz = 128):'''用梯度上升法做训练'''self.batch_sz = batch_szerr_list = []for epoch in range(epochs):#初始化data loaderself.train_loader(X_train)err_sum = 0while 1:v0_prob = self.get_batch()if type(v0_prob)==type(None):breaksize = len(v0_prob)dW = np.zeros_like(self.W)dbv = np.zeros_like(self.bv)dbh = np.zeros_like(self.bh)#for v0_prob in  batch_data:h0_prob = self.forword(v0_prob)             h0 = np.zeros_like(h0_prob)h0[h0_prob > np.random.random(h0_prob.shape)] = 1v1_prob = self.backward(h0)v1 = np.zeros_like(v1_prob)v1[v1_prob > np.random.random(v1_prob.shape)] = 1h1_prob = self.forword(v1)h1 = np.zeros_like(h1_prob)                                        h1[h1_prob > np.random.random(h1_prob.shape)] = 1dW = np.dot(h0.T , v0_prob) - np.dot(h1.T , v1_prob)dbv = np.sum(v0_prob - v1_prob,axis = 0)dbh = np.sum(h0_prob - h1_prob,axis = 0)err_sum += np.mean(np.sum((v0_prob - v1_prob)**2,axis=1))dW /= sizedbv /= sizedbh /= sizeself.W += dW*self.lrself.bv += dbv*self.lrself.bh += dbh*self.lrerr_sum = err_sum / len(X_train)err_list.append(err_sum)print('Epoch {0},err_sum {1}'.format(epoch, err_sum))plt.plot(err_list)def predict(self,input_x):h0_prob = self.forword(input_x)                h0 = np.zeros_like(h0_prob)h0[h0_prob > np.random.random(h0_prob.shape)] = 1v1 = self.backward(h0)return v1

这里用了batch技巧加速运算，也就是把单次计算的矩阵-向量乘法变成多次计算的矩阵-矩阵乘法，因为矩阵越大，乘法越容易并行化，速度也就越快。其他细节只需要按照上面的算法敲就好了。
我们看一看训练的效果

rbm = RBM()
rbm.fit(data,epochs=30)

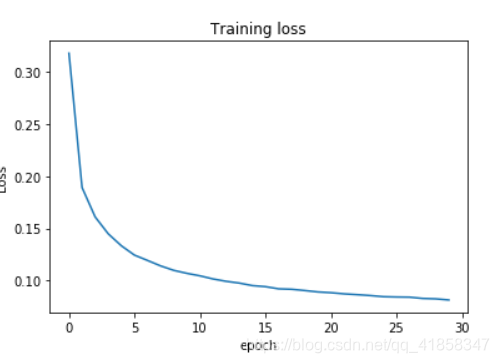
在这里插入图片描述
用RBM尝试重建MNIST图片

def visualize(input_x):plt.figure(figsize=(5,5), dpi=180)for i in range(0,8):for j in range(0,8):img = input_x[i*8+j].reshape(28,28)plt.subplot(8,8,i*8+j+1)plt.imshow(img ,cmap = plt.cm.gray) #显示64张手写数字 
images = data[0:64]
visualize(images)#显示重构的图像
rebuild_value = [rbm.predict(x) for x in images]
visualize(rebuild_value)

在这里插入图片描述

我们还可以拿出它的隐层作为降维后的结果。

总结

自己实现完后会发现AutoEncoder与RBM非常像：
（1）参数一样：隐含层偏置、显示层偏置、网络权重
（2）作用一样：都是输入的另一种（压缩）表示
（3）过程类似：都有reconstruct，并且都是reconstruct与input的差别，越小越好
事实上两者还是有区别的，在训练方法上，RBM最小化对数似然函数，AE最小化重建误差，虽然效果相似，但是它们是两种不同理念的模型。
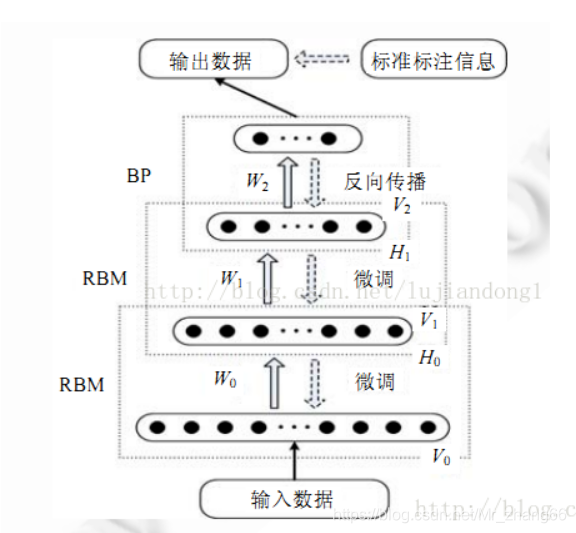
RBM更大的作用还是在搭建DBN网络上，这也是一种很强的生成模型。不知道我还有没有机会学习DBN，如果有机会，将来还会再写一篇博客。
谢谢阅读