RBM

关于受限玻尔兹曼机RBM，网上很多博客[1][2]都总结推导RBM很详细，很少有人能通俗地解释一下RBM的用途和有点，我觉得[2]写得很好，可以参考辅助理解，下面简单总结一下我的理解和一些相关知识。

网络结构

RBM是一个无监督拟合训练数据分布的一种方法。包含两层，可视层(V)和隐藏层(H)。层与层之间是全连接，层内部每个节点互相独立，参数包含（W,a,b）。网络结构比较简单，给定训练数据可以通过W将v和h相互转换。

优化目标

首先引入能量函数，在一个无监督的方法中，我们的优化目标是什么呢？受统计力学的启发，整个概率图引入能量函数来描述稳定状态，在RBM中，是由可视层能量、隐藏层能量和连接部分能量构成的。

由能量函数可以定义(v,h)出现的联合概率，

实际上我们关心的是P(v)的分布，也就是上式的边缘分布，由能量函数和联合概率的定义可以推出可视层和隐藏层转换的公式，详细推导可参考[1],


至此，我们可以根据每个训练数据v求得h，也可由h计算v，那么我们怎么根据目标函数优化W、a、b呢？

其实就是最大化似然函数，之所以最大化似然函数就是让已知数据出现的概率最高来拟合训练数据吧？给定训练集合S={v1,v2…vn}，最大化所有P(vi)的乘积，取ln就变成最大化下面的似然函数：

有了目标函数进行求梯度进行优化，但是在求梯度的过程中涉及到(v,h)的联合概率分布，需要把v、h的各种组合穷举一遍，复杂度太高，因此采用Gibbs sampling来估计。考虑到每次迭代更新都要进行Gibbs sampling迭代很多次达到稳定，并且需要大量的采样数据，所以Hinton老先生提出了对比散度算法(COntrasive Divergence)。

对比散度算法CD-K

GIbbs sampling 需要迭代很多次才能收敛，Hinton提出直接用训练样本来初始化起始状态，然后迭代采样，一般一步就可以得到较好的结果。算法流程如下图：

其中两个采样函数就是根据前面可视层和隐藏层的转换来采样的，有转换公式可以得到h或v每个节点的概率（0-1之间，因为过了sigmoid），所以随机生成一个0-1之间的随机数，小于该节点的概率就是1，大于就是0。

模型训练

构建好网络结构，得到目标函数，即可求梯度对训练数据优化模型参数了。
具体训练算法流程如下：

由此，可以训练一个RBM的网络来拟合我们的训练数据。RBM主要是构建了(v,h)之间的联合分布，根据这个联合分布我们可以用来做分类、降维、参数预训练等等。传说autoEncoder和RBM预训练初始化参数会很好地提升模型的结果，RBM可以预训练参数矩阵和a，b，没试过~可以尝试一发。

DBN

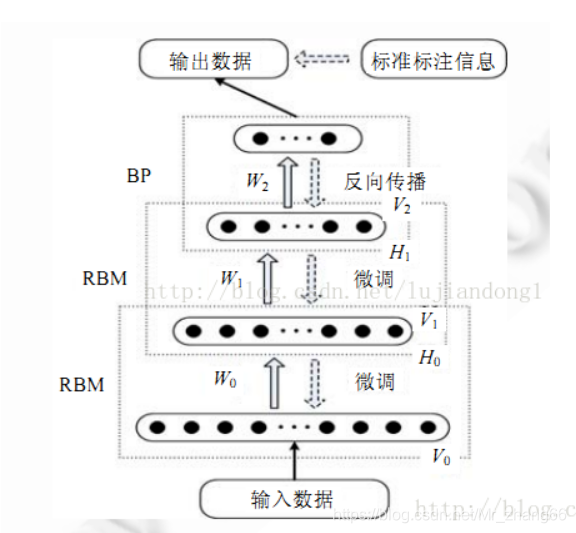
深度置信网络(Deep Belief Network)，可用作非监督学习，类似于自编码器，也可用于分类。
DBN就是将多个RBM堆叠起来，前一个RBM的隐藏层作为下一个RBM的可视层，每次训练时，将下层的RBM训练好后再训练上层的RBM，每次训练一层，直至最后。

参考博客:
[1]https://blog.csdn.net/itplus/article/details/19168937
[2]https://zhuanlan.zhihu.com/p/31107178