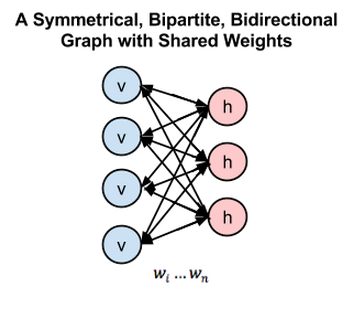
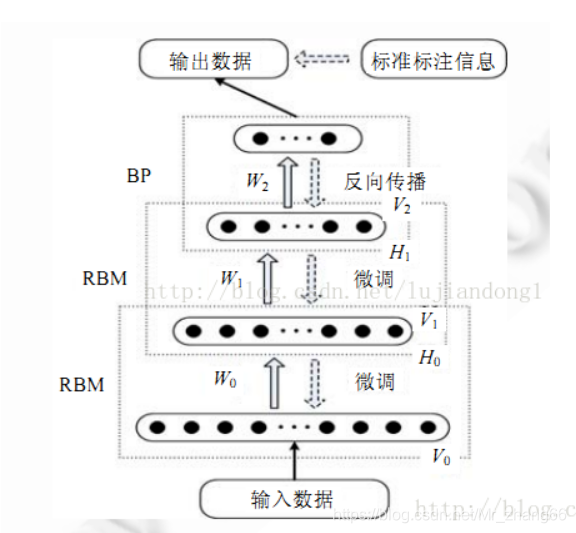
受限玻尔兹曼机是一种可用随机神经网络来解释的概率图模型。它由Smolensky于1986年在玻尔兹曼机（BM）的基础上提出，所谓“随机”，是指这种网络中的神经元是随机神经元，其输出只有两种状态（激活和未激活），一般用二进制的0和1来表示，而状态的具体取值则根据概率统计法则来决定。

随着计算机计算性能的迅速提高和快速算法的不断发展，RBM在各种相关机器学习算法中已经变得实际可行。尤其是，在Hinton于2006年提出了以RBM为基本构成模块的DBN模型之后，机器学习更是掀起了一股研究RBM理论及应用的热潮。

本文首先讲述RBM模型所涉及到的预备知识点：

1、sigmoid函数

sigmoid函数是神经网络中常用的激活函数之一，其定义为：

该函数的定义域为，值域为(0,1)。下图为sigmoid函数的图像。

2、Bayes定理

贝叶斯定理是英国数学家贝叶斯提出来的，用来描述两个条件概率之间的关系。若记P(A),P(B)分别表示事件A和B发生的概率，P(A|B)表示事件B发生的情况下事件A发生的概率，P(A，B)表示事件A、B同时发生的概率，则有

进一步推导可得：

这就是贝叶斯公式。上式中我们把P(A)称为“先验概率”（prior probability），即在事件B发生之前，我们对事件A发生概率的一个判断。P(A|B)称为“后验概率”（Posterior probability），即在事件B发生之后，我们对事件A发生概率的重新评估。

称为“可能性函数”（likelyhood），这是一个调整因子，使得预估概率更接近真实概率。

3、二分图

二分图又称二部图、双分图或偶图，是图论中的一种特殊模型。设是一个无向图，如果顶点V可分割为两个互不相交的子集V_1和V_2，并且图中每条边（i,j）所关联的两个顶点i和j分别属于这两个不同的顶点集，则称图G为一个二分图。

4、MCMC方法

最早的蒙特卡罗方法是由物理学家发明的，旨在于通过随机化的方法计算积分，假设给定函数h(x)，我们想计算如下的积分：

如果我们无法通过数学推导直接求出解析解，那么，为了避免对区间（a，b）上所有的x值进行枚举（多数情况下这也是不可能的），我们可以将h(x)分解为某个函数f(x)和一个定义在（a，b）上的概率密度函数p(x)的乘积。这样整个积分就可以写成

这样一来原积分就等同于f(x)在p(x)这个分布上的均值。这时，如果我们从分布p(x)上采集大量的样本点，这些样本符合分布p(x)，即对所有的i，有

那么，我们就可以通过这些样本来逼近这个均值

这就是蒙特卡罗方法的思想。近年来，随着随机化模型的流行，蒙特卡罗方法在机器学习领域有着越来越广泛的应用。

假如我们现在已经定义好分布p(x)，那么，蒙特卡罗方法的一个核心问题是：如何从这个分布上采集样本？

一般来讲，对于经典的分布，例如对于均匀分布和正态分布等，都已经有比较成熟的算法可以快速地直接生成该分布下的无偏样本。然而，对于任意的分布，我们并不能做到这一点。那么，如何在任意分布下采样？这就是马尔科夫链蒙特卡罗方法（MCMC）需要解决的问题。

简单来说，MCMC的思想就是利用马尔科夫链来产生指定分布下的样本。为此，先简单介绍一下马尔科夫链的基本知识。

5、马尔可夫链

设X_t表示随机变量X在离散时间t时刻的取值。若该变量随时间变化的转移概率仅仅依赖于它的当前取值，即：

则称这个变量为马尔可夫变量，其中具有马尔可夫性质的随机过程称为马尔可夫过程。

由上式可知，对于一个马尔可夫随机变量，我们只需要知道其当前的取值，就足以充分预测其未来的变化趋势。而所谓的马尔可夫链就是指一段时间内随机变量X的取值序列符合上式条件。

一般来说，一个马尔可夫链可通过其对应的转移概率来定义。所谓转移概率，是指随机变量从一个时刻到下一个时刻，从状态s_i转移到另一个状态s_j的概率，即

若记表示随机变量X在时刻t取值s_k的概率，则X在时刻t+1取值为s_i的概率为：

设状态的数目为n，则有

上式也可以写成矩阵向量形式

其中，为行向量，为转移概率矩阵。

如果存在某个取值，从它出发转移回自身所需要的转移次数总是整数d（>1）的倍数，那么这个马尔可夫过程就具有周期性。如果任意两个数值之间总是能以非0的概率的相互转移，那么该马尔可夫过程就称为不可约（“不可约”是指每一个状态都可来自任意的其他状态）。如果一个马尔可夫过程既没有周期性，又不可约，则称它是各态遍历的。

6、正则分布

其中：

7、Metropolis-Hastings采样

8、Gibbs采样