受限玻尔兹曼机(RBM)
一、RBM的网络结构
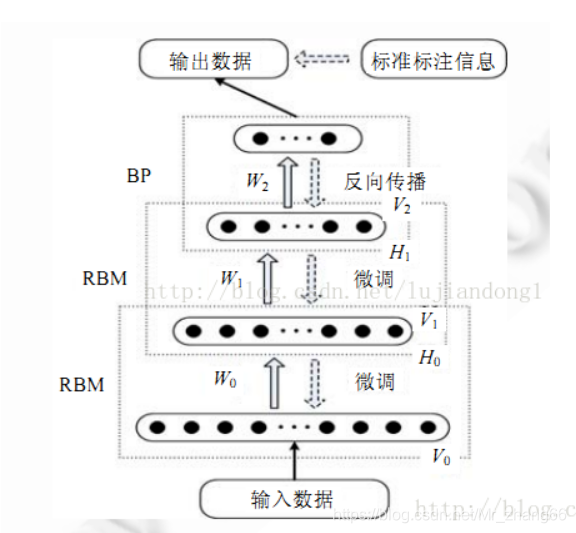
RBM的网络结构如下图所示:
RBM中包括两层,即:
- 可见层(visible layer),图上的___v___
- 隐藏层(hidden layer),图上的___h___
由上图可知,在同一层中,如上图中的可见层,在可见层中,其节点之间是没有连接的,而在层与层之间,其节点是全连接的,这是RBM最重要的结构特征:层内无连接,层间全连接。
在RBM的模型中,有如下的性质:
当给定可见层神经元的状态时。各隐藏层神经元的之间是否激活是条件独立的;反之也同样成立。
下面给出RBM模型的数学化定义:
如图:
假设可见层的神经元的个数为 n v n_v nv,隐藏层的神经元的个数为 n h n_h nh,
- v v v 表示的是可见层神经元的状态, v = ( v 1 , v 2 , ⋯ , v n v ) T v=(v_1,v_2,⋯,v_{n_v})^T v=(v1,v2,⋯,vnv)T。
- h h h 表示的是隐藏层神经元的状态, h = ( h 1 , h 2 , ⋯ , h n h ) T h=(h_1,h_2,⋯,h_{n_h})^T h=(h1,h2,⋯,hnh)T。
- a a a 表示的是可见层神经元的偏置, a = ( a 1 , a 2 , ⋯ , a n v ) T ∈ R n v a=(a_1,a_2,⋯,a_{n_v})^T∈{R}^{n_v} a=(a1,a2,⋯,anv)T∈Rnv。
- b b b 表示的是隐藏层神经元的偏置, b = ( b 1 , b 2 , ⋯ , b n h ) T ∈ R n h b=(b_1,b_2,⋯,b_{n_h})^T∈{R}^{n_h} b=(b1,b2,⋯,bnh)T∈Rnh。
- W = ( w i , j ) ∈ R n h × n v W=(w_{i,j})∈R^{nh×nv} W=(wi,j)∈Rnh×nv表示的是隐藏层与可见层之间的连接权重。
同时,我们记 θ = ( W , a , b ) \theta=(W,a,b) θ=(W,a,b)。
二、RBM模型的计算
2.1、能量函数
对于一组给定的状态 ( v , h ) (v,h) (v,h),定义如下的能量函数:
E θ ( v , h ) = − ∑ i = 1 n v a i v i − ∑ j = 1 n h b j h j − ∑ i = 1 n v ∑ j = 1 n h h j w j , i v i E_{\theta}(\mathbf{v}, \mathbf{h})=-\sum_{i=1}^{n_{v}} a_{i} v_{i}-\sum_{j=1}^{n_{h}} b_{j} h_{j}-\sum_{i=1}^{n_{v}} \sum_{j=1}^{n_{h}} h_{j} w_{j, i} v_{i} Eθ(v,h)=−i=1∑nvaivi−j=1∑nhbjhj−i=1∑nvj=1∑nhhjwj,ivi
利用该能量公式,可以定义如下的联合概率分布:
P θ ( v , h ) = 1 Z θ e − E θ ( v , h ) P_{\theta}(\mathbf{v}, \mathbf{h})=\frac{1}{Z_{\theta}} e^{-E_{\theta}(\mathbf{v}, \mathbf{h})} Pθ(v,h)=Zθ1e−Eθ(v,h)
其中:
Z θ = ∑ v , h e − E θ ( v , h ) Z_{\theta}=\sum_{\mathbf{v}, \mathbf{h}} e^{-E_{\theta}(\mathbf{v}, \mathbf{h})} Zθ=v,h∑e−Eθ(v,h)
称为归一化因子。
当有了联合概率分布,我们便可以定义边缘概率分布,即:
P θ ( v ) = ∑ h P θ ( v , h ) = 1 Z θ ∑ h e − E θ ( v , h ) P θ ( h ) = ∑ v P θ ( v , h ) = 1 Z θ ∑ v e − E θ ( v , h ) \begin{aligned} &P_{\theta}(\mathbf{v})=\sum_{\mathbf{h}} P_{\theta}(\mathbf{v}, \mathbf{h})=\frac{1}{Z_{\theta}} \sum_{\mathbf{h}} e^{-E_{\theta}(\mathbf{v}, \mathbf{h})} \\ &P_{\theta}(\mathbf{h})=\sum_{\mathbf{v}} P_{\theta}(\mathbf{v}, \mathbf{h})=\frac{1}{Z_{\theta}} \sum_{\mathbf{v}} e^{-E_{\theta}(\mathbf{v}, \mathbf{h})} \end{aligned} Pθ(v)=h∑Pθ(v,h)=Zθ1h∑e−Eθ(v,h)Pθ(h)=v∑Pθ(v,h)=Zθ1v∑e−Eθ(v,h)
2.2、激活概率
有了上述的联合概率分布以及边缘概率分布,我们需要知道当给定可见层的状态时,隐藏层上的某一个神经元被激活的概率,即 P ( h k = 1 ∣ v ) P(h_k=1\mid v) P(hk=1∣v),或者当给定了隐藏层的状态时,可见层上的某一神经元被激活的概率,即 P ( v k = 1 ∣ h ) P(v_k=1\mid h) P(vk=1∣h)。
首先定义如下的一些标记:
h − k ≜ ( h 1 , h 2 , ⋯ , h k − 1 , h k + 1 , ⋯ , h n h ) T \mathbf{h}_{-k} \triangleq\left(h_{1}, h_{2}, \cdots, h_{k-1}, h_{k+1}, \cdots, h_{n_{h}}\right)^{T} h−k≜(h1,h2,⋯,hk−1,hk+1,⋯,hnh)T
上式表示的是在h中去除了分量 h k h_k hk后得到的向量。
α k ( v ) ≜ b k + ∑ i = 1 n v w k , i v i \mathbf{\alpha}_{k}(v) \triangleq b_{k}+\sum_{i=1}^{n_v} w_{k, i} v_{i} αk(v)≜bk+i=1∑nvwk,ivi
β ( v , h − k ) ≜ ∑ i = 1 n v a i v i + ∑ j = 1 , j ≠ k n h b j h j + ∑ i = 1 n v ∑ j = 1 , j ≠ k n h h j w j , i v i \beta\left(\mathbf{v}, \mathbf{h}_{-k}\right) \triangleq \sum_{i=1}^{n_{v}} a_{i} v_{i}+\sum_{j=1, j \neq k}^{n_{h}} b_{j} h_{j}+\sum_{i=1}^{n_{v}} \sum_{j=1, j \neq k}^{n_{h}} h_{j} w_{j, i} v_{i} β(v,h−k)≜i=1∑nvaivi+j=1,j=k∑nhbjhj+i=1∑nvj=1,j=k∑nhhjwj,ivi
有了如上的一些公式,我们可以得到能量公式的如下表示方法:
E ( v , h ) = − β ( v , h k ) − h k α k ( v ) E(v,h)=−\beta(v,h_k)−h_k\alpha_k(v) E(v,h)=−β(v,hk)−hkαk(v)
那么,当给定可见层的状态时,隐藏层上的某一个神经元被激活的概率 P ( h k = 1 ∣ v ) P(h_k=1\mid v) P(hk=1∣v)为:
P ( h k = 1 ∣ v ) = P ( h k = 1 ∣ h − k , v ) = P ( h k = 1 , h − k , v ) P ( h − k , v ) = P ( h k = 1 , h − k , v ) P ( h k = 0 , h − k , v ) + P ( h k = 1 , h − k , v ) = e − E ( h k = 1 , h − k v ) e − E ( h k = 0 , h − k v ) + e − E ( h k = 1 , h − k v ) = 1 1 + e − E ( h k = 0 , h − k v ) + E ( h k = 1 , h − h 0 v ) = 1 1 + e [ β ( v , h − k ) + 0 ⋅ α k ( v ) ] + [ − β ( v , h − k ) − 1 ⋅ α k ( v ) ] = 1 1 + e − α k ( v ) \begin{aligned} P\left(h_{k}=1 \mid \mathbf{v}\right)&=P\left(h_{k}=1 \mid \mathbf{h}_{-k}, \mathbf{v}\right)\\ &=\frac{P\left(h_{k}=1, \mathbf{h}_{-k}, \mathbf{v}\right)}{P\left(\mathbf{h}_{-k}, \mathbf{v}\right)}\\ &=\frac{P\left(h_{k}=1, \mathbf{h}_{-k}, \mathbf{v}\right)}{P\left(h_{k}=0, \mathbf{h}_{-k}, \mathbf{v}\right)+P\left(h_{k}=1, \mathbf{h}_{-k}, \mathbf{v}\right)}\\ &=\frac{e^{-E\left(h_{k}=1, \mathbf{h}_{-k} \mathbf{v}\right)}}{e^{-E\left(h_{k}=0, \mathbf{h}_{-k} \mathbf{v}\right)}+e^{-E\left(h_{k}=1, \mathbf{h}_{-k} \mathbf{v}\right)}}\\ &=\frac{1}{1+e^{-E\left(h_{k}=0, \mathbf{h}_{-k} \mathbf{v}\right)+E\left(h_{k}=1, \mathbf{h}_{-h_{0}} \mathbf{v}\right)}}\\ &=\frac{1}{1+e^{\left[\beta\left(\mathbf{v}, \mathbf{h}^{-k}\right)+0 \cdot \alpha_{k}(\mathbf{v})\right]+\left[-\beta\left(\mathbf{v}, \mathbf{h}^{-k}\right)-1 \cdot \alpha_{k}(\mathbf{v})\right]}}\\ &=\frac{1}{1+e^{-\alpha_{k}(\mathbf{v})}} \end{aligned} P(hk=1∣v)=P(hk=1∣h−k,v)=P(h−k,v)P(hk=1,h−k,v)=P(hk=0,h−k,v)+P(hk=1,h−k,v)P(hk=1,h−k,v)=e−E(hk=0,h−kv)+e−E(hk=1,h−kv)e−E(hk=1,h−kv)=1+e−E(hk=0,h−kv)+E(hk=1,h−h0v)1=1+e[β(v,h−k)+0⋅αk(v)]+[−β(v,h−k)−1⋅αk(v)]1=1+e−αk(v)1
由Sigmoid函数可知:
S i g m o i d ( x ) = 1 1 + e − x {Sigmoid(x)}=\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1
则:
P ( h k = 1 ∣ v ) = Sigmoid ( α k ( v ) ) = Sigmoid ( b k + ∑ i = 1 n v w k , i v i ) \begin{aligned} P\left(h_{k}=1 \mid \mathbf{v}\right) &=\operatorname{Sigmoid}\left(\alpha_{k}(\mathbf{v})\right) \\ &=\operatorname{Sigmoid}\left(b_{k}+\sum_{i=1}^{n_{v}} w_{k, i} v_{i}\right) \end{aligned} P(hk=1∣v)=Sigmoid(αk(v))=Sigmoid(bk+i=1∑nvwk,ivi)
同理,可以求得当给定了隐藏层的状态时,可见层上的某一神经元被激活的概率 P ( v k = 1 ∣ h ) P(v_k=1\mid h) P(vk=1∣h):
P ( v k = 1 ∣ h ) = Sigmoid ( α k ( h ) ) = Sigmoid ( a k + ∑ j = 1 n h w j , k h j ) \begin{aligned} P\left(v_{k}=1 \mid \mathbf{h}\right) &=\operatorname{Sigmoid}\left(\alpha_{k}(\mathbf{h})\right) \\ &=\operatorname{Sigmoid}\left(a_{k}+\sum_{j=1}^{n_{h}} w_{j, k} h_{j}\right) \end{aligned} P(vk=1∣h)=Sigmoid(αk(h))=Sigmoid(ak+j=1∑nhwj,khj)
2.3、模型的训练
2.3.1模型的优化函数
对于RBM模型,其参数主要是可见层和隐藏层之间的权重,可见层的偏置以及隐藏层的偏置,即 θ = ( W , a , b ) \theta=(W,a,b) θ=(W,a,b),对于给定的训练样本,通过训练得到参数 θ \theta θ,使得在该参数下,由RBM表示的概率分布尽可能与训练数据相符合。
假设给定的训练集为:
X = { v 1 , v 2 , ⋯ , v n s } \mathbf{X}=\lbrace{v^1,v^2,\cdots,v^{n_s}}\rbrace X={v1,v2,⋯,vns}
其中, n s n_s ns表示的是训练样本的数目, v i = ( v 1 i , v 2 i , ⋯ , v n v i ) T v^i=(v^i_1,v^i_2,\cdots,v^i_{n_v})^T vi=(v1i,v2i,⋯,vnvi)T。为了能够学习出模型中的参数,我们希望利用模型重构出来的数据能够尽可能与原始数据一致,则训练RBM的目标就是最大化如下的似然函数:
L θ = ∏ i = 1 n s P ( v i ) L_{\theta}=\prod_{i=1}^{n_{s}} P\left(\mathbf{v}^{i}\right) Lθ=i=1∏nsP(vi)
对于如上的似然函数的最大化问题,通常是取其log函数的形式:
ln L θ = ln ∏ i = 1 n s P ( v i ) = ∑ i = 1 n s ln P ( v i ) \ln L_{\theta}=\ln \prod_{i=1}^{n_{s}} P\left(\mathbf{v}^{i}\right)=\sum_{i=1}^{n_{s}} \ln P\left(\mathbf{v}^{i}\right) lnLθ=lni=1∏nsP(vi)=i=1∑nslnP(vi)
2.3.2、最大似然的求解
对于上述的最优化问题,可以使用梯度上升法进行求解,梯度上升法的形式为:
θ = θ + η ∂ ln L θ ∂ θ \theta=\theta+\eta \frac{\partial \ln L_{\theta}}{\partial \theta} θ=θ+η∂θ∂lnLθ
其中,η>0称为学习率。对于 ∂ ln L θ ∂ θ \frac{\partial \ln L_{\theta}}{\partial \theta} ∂θ∂lnLθ的求解,简单的情况,只考虑一个样本的情况,则:
ln L θ = ln P ( v ) = ln ( 1 Z ∑ h e − E ( v , h ) ) = ln ∑ h e − E ( v , h ) − ln Z = ln ∑ h e − E ( v , h ) − ln ∑ v , h e − E ( v , h ) \begin{aligned} \ln L_{\theta} &=\ln P(\mathbf{v}) \\ &=\ln \left(\frac{1}{Z} \sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}\right) \\ &=\ln \sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}-\ln Z \\ &=\ln \sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}-\ln \sum_{\mathbf{v}, \mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})} \end{aligned} lnLθ=lnP(v)=ln(Z1h∑e−E(v,h))=lnh∑e−E(v,h)−lnZ=lnh∑e−E(v,h)−lnv,h∑e−E(v,h)
则 ∂ ln L θ ∂ θ \frac{\partial \ln L_{\theta}}{\partial \theta} ∂θ∂lnLθ为:
∂ ln L θ ∂ θ = ∂ ln P ( v ) ∂ θ = ∂ ∂ θ ( ln ∑ h e − E ( v , h ) ) − ∂ ∂ θ ( ln ∑ v , h e − E ( v , h ) ) = − 1 ∑ h e − E ( v , h ) ∑ h e − E ( v , h ) ∂ E ( v , h ) ∂ θ + 1 ∑ v , h e − E ( v , h ) ∑ v , h e − E ( v , h ) ∂ E ( v , h ) ∂ θ \begin{aligned} \frac{\partial \ln L_{\theta}}{\partial \theta} &=\frac{\partial \ln P(\mathbf{v})}{\partial \theta} \\ &=\frac{\partial}{\partial \theta}\left(\ln \sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}\right)-\frac{\partial}{\partial \theta}\left(\ln \sum_{\mathbf{v}, \mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}\right) \\ &=-\frac{1}{\sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}} \sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})} \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta}+\frac{1}{\sum_{\mathbf{v}, \mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}} \sum_{\mathbf{v}, \mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})} \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} \end{aligned} ∂θ∂lnLθ=∂θ∂lnP(v)=∂θ∂(lnh∑e−E(v,h))−∂θ∂⎝⎛lnv,h∑e−E(v,h)⎠⎞=−∑he−E(v,h)1h∑e−E(v,h)∂θ∂E(v,h)+∑v,he−E(v,h)1v,h∑e−E(v,h)∂θ∂E(v,h)
而:
e − E ( v , h ) ∑ h e − E ( v , h ) = e − E ( v , h ) Z ∑ h e − E ( v , h ) Z = P ( v , h ) P ( v ) = P ( h ∣ v ) \frac{e^{-E(\mathbf{v}, \mathbf{h})}}{\sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}}=\frac{\frac{e^{-E(\mathbf{v}, \mathbf{h})}}{Z}}{\frac{\sum_{\mathbf{h}} e^{-E(\mathbf{v}, \mathbf{h})}}{Z}}=\frac{P(\mathbf{v}, \mathbf{h})}{P(\mathbf{v})}=P(\mathbf{h} \mid \mathbf{v}) ∑he−E(v,h)e−E(v,h)=Z∑he−E(v,h)Ze−E(v,h)=P(v)P(v,h)=P(h∣v)
因此上式可以表示为:
∂ ln L θ ∂ θ = − ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ θ + ∑ v , h P ( v , h ) ∂ E ( v , h ) ∂ θ \frac{\partial \ln L_{\theta}}{\partial \theta}=-\sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta}+\sum_{\mathbf{v}, \mathbf{h}} P(\mathbf{v}, \mathbf{h}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∂θ∂lnLθ=−h∑P(h∣v)∂θ∂E(v,h)+v,h∑P(v,h)∂θ∂E(v,h)
其中, ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ θ \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∑hP(h∣v)∂θ∂E(v,h)表示的是能量梯度函数, ∂ E ( v , h ) ∂ θ \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∂θ∂E(v,h)在条件分布 P ( h ∣ v ) P(\mathbf{h} \mid \mathbf{v}) P(h∣v)的期望; ∑ v , h P ( v , h ) ∂ E ( v , h ) ∂ θ \sum_{\mathbf{v}, \mathbf{h}} P(\mathbf{v}, \mathbf{h}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∑v,hP(v,h)∂θ∂E(v,h)表示的是能量梯度函数, ∂ E ( v , h ) ∂ θ \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∂θ∂E(v,h)在联合分布 P ( v , h ) P(v,h) P(v,h)下的期望。
对于 ∑ v , h P ( v , h ) ∂ E ( v , h ) ∂ θ \sum_{\mathbf{v}, \mathbf{h}} P(\mathbf{v}, \mathbf{h}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∑v,hP(v,h)∂θ∂E(v,h),可以表示为:
∑ v , h P ( v , h ) ∂ E ( v , h ) ∂ θ = ∑ v ∑ h P ( v ) P ( h ∣ v ) ∂ E ( v , h ) ∂ θ = ∑ v P ( v ) ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ θ \begin{aligned} \sum_{\mathbf{v}, \mathbf{h}} P(\mathbf{v}, \mathbf{h}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} &=\sum_{\mathbf{v}} \sum_{\mathbf{h}} P(\mathbf{v}) P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} \\ &=\sum_{\mathbf{v}} P(\mathbf{v}) \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} \end{aligned} v,h∑P(v,h)∂θ∂E(v,h)=v∑h∑P(v)P(h∣v)∂θ∂E(v,h)=v∑P(v)h∑P(h∣v)∂θ∂E(v,h)
因此,只需要计算 ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ θ \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial \theta} ∑hP(h∣v)∂θ∂E(v,h),这部分的计算分为三个,分别为:
- ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ w i , j \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial w_{i,j}} ∑hP(h∣v)∂wi,j∂E(v,h)
- ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ a i \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial a_{i}} ∑hP(h∣v)∂ai∂E(v,h)
- ∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ b j \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial b_{j}} ∑hP(h∣v)∂bj∂E(v,h)
上述的三个部分计算的方法如下:
已知:
E θ ( v , h ) = − ∑ i = 1 n v a i v i − ∑ j = 1 n h b j h j − ∑ i = 1 n v ∑ j = 1 n h h j w j , i v i E_{\theta}(\mathbf{v}, \mathbf{h})=-\sum_{i=1}^{n_{v}} a_{i} v_{i}-\sum_{j=1}^{n_{h}} b_{j} h_{j}-\sum_{i=1}^{n_{v}} \sum_{j=1}^{n_{h}} h_{j} w_{j, i} v_{i} Eθ(v,h)=−i=1∑nvaivi−j=1∑nhbjhj−i=1∑nvj=1∑nhhjwj,ivi
则:
- 对 w j , i w_{j,i} wj,i求导数
∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ w j , i = − ∑ h P ( h ∣ v ) h j v i = − ∑ h ∏ k = 1 n h P ( h k ∣ v ) h j v i = − ∑ h P ( h j ∣ v ) P ( h − j ∣ v ) h j v i = − ∑ h j P ( h j ∣ v ) h j v i ∑ h − j P ( h − j ∣ v ) = − ∑ h j P ( h j ∣ v ) h j v i = − ( P ( h j = 0 ∣ v ) ⋅ 0 ⋅ v i + P ( h j = 1 ∣ v ) ⋅ 1 ⋅ v i ) = − P ( h j = 1 ∣ v ) v i \begin{aligned} \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial w_{j, i}} &=-\sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) h_{j} v_{i} \\ &=-\sum_{\mathbf{h}} \prod_{k=1}^{n_{h}} P\left(h_{k} \mid \mathbf{v}\right) h_{j} v_{i} \\ &=-\sum_{\mathbf{h}} P\left(h_{j} \mid \mathbf{v}\right) P\left(\mathbf{h}_{-j} \mid \mathbf{v}\right) h_{j} v_{i} \\ &=-\sum_{h_{j}} P\left(h_{j} \mid \mathbf{v}\right) h_{j} v_{i} \sum_{\mathbf{h}_{-j}} P\left(\mathbf{h}_{-j} \mid \mathbf{v}\right) \\ &=-\sum_{h_{j}} P\left(h_{j} \mid \mathbf{v}\right) h_{j} v_{i} \\ &=-\left(P\left(h_{j}=0 \mid \mathbf{v}\right) \cdot 0 \cdot v_{i}+P\left(h_{j}=1 \mid \mathbf{v}\right) \cdot 1 \cdot v_{i}\right) \\ &=-P\left(h_{j}=1 \mid \mathbf{v}\right) v_{i} \end{aligned} h∑P(h∣v)∂wj,i∂E(v,h)=−h∑P(h∣v)hjvi=−h∑k=1∏nhP(hk∣v)hjvi=−h∑P(hj∣v)P(h−j∣v)hjvi=−hj∑P(hj∣v)hjvih−j∑P(h−j∣v)=−hj∑P(hj∣v)hjvi=−(P(hj=0∣v)⋅0⋅vi+P(hj=1∣v)⋅1⋅vi)=−P(hj=1∣v)vi
- 对 a i a_{i} ai求导数
∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ a i = − ∑ h P ( h ∣ v ) v i = − v i ∑ h P ( h ∣ v ) = − v i \begin{aligned} \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial a_{i}} &=-\sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) v_{i} \\ &=-v_{i} \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \\ &=-v_{i} \end{aligned} h∑P(h∣v)∂ai∂E(v,h)=−h∑P(h∣v)vi=−vih∑P(h∣v)=−vi
- 对 b j b_{j} bj求导数
∑ h P ( h ∣ v ) ∂ E ( v , h ) ∂ b j = − ∑ h P ( h ∣ v ) h j = − ∑ h ∏ k = 1 n h P ( h k ∣ v ) h j = − ∑ h P ( h j ∣ v ) P ( h − j ∣ v ) h j = − ∑ h j P ( h j ∣ v ) h j ∑ h − j P ( h − j ∣ v ) = − ∑ h j P ( h j ∣ v ) h j = − ( P ( h j = 0 ∣ v ) ⋅ 0 + P ( h j = 1 ∣ v ) ⋅ 1 ) = − P ( h j = 1 ∣ v ) \begin{aligned} \sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) \frac{\partial E(\mathbf{v}, \mathbf{h})}{\partial b_{j}} &=-\sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}) h_{j} \\ &=-\sum_{\mathbf{h}} \prod_{k=1}^{n_{h}} P\left(h_{k} \mid \mathbf{v}\right) h_{j} \\ &=-\sum_{\mathbf{h}} P\left(h_{j} \mid \mathbf{v}\right) P\left(\mathbf{h}_{-j} \mid \mathbf{v}\right) h_{j} \\ &=-\sum_{h_{j}} P\left(h_{j} \mid \mathbf{v}\right) h_{j} \sum_{\mathbf{h}_{-j}} P\left(\mathbf{h}_{-j} \mid \mathbf{v}\right) \\ &=-\sum_{h_{j}} P\left(h_{j} \mid \mathbf{v}\right) h_{j} \\ &=-\left(P\left(h_{j}=0 \mid \mathbf{v}\right) \cdot 0+P\left(h_{j}=1 \mid \mathbf{v}\right) \cdot 1\right) \\ &=-P\left(h_{j}=1 \mid \mathbf{v}\right) \end{aligned} h∑P(h∣v)∂bj∂E(v,h)=−h∑P(h∣v)hj=−h∑k=1∏nhP(hk∣v)hj=−h∑P(hj∣v)P(h−j∣v)hj=−hj∑P(hj∣v)hjh−j∑P(h−j∣v)=−hj∑P(hj∣v)hj=−(P(hj=0∣v)⋅0+P(hj=1∣v)⋅1)=−P(hj=1∣v)
因此, ∂ ln L θ ∂ θ \frac{\partial \ln L_{\theta}}{\partial \theta} ∂θ∂lnLθ为:
∂ ln L θ ∂ w j , i = P ( h j = 1 ∣ v ) v i − ∑ v P ( v ) P ( h j = 1 ∣ v ) v i ∂ ln L θ ∂ a i = v i − ∑ v P ( v ) v i ∂ ln L θ ∂ b j = P ( h j = 1 ∣ v ) − ∑ v P ( v ) P ( h j = 1 ∣ v ) \begin{gathered} \frac{\partial \ln L_{\theta}}{\partial w_{j, i}}=P\left(h_{j}=1 \mid \mathbf{v}\right) v_{i}-\sum_{\mathbf{v}} P(\mathbf{v}) P\left(h_{j}=1 \mid \mathbf{v}\right) v_{i} \\ \frac{\partial \ln L_{\theta}}{\partial a_{i}}=v_{i}-\sum_{\mathbf{v}} P(\mathbf{v}) v_{i} \\ \frac{\partial \ln L_{\theta}}{\partial b_{j}}=P\left(h_{j}=1 \mid \mathbf{v}\right)-\sum_{\mathbf{v}} P(\mathbf{v}) P\left(h_{j}=1 \mid \mathbf{v}\right) \end{gathered} ∂wj,i∂lnLθ=P(hj=1∣v)vi−v∑P(v)P(hj=1∣v)vi∂ai∂lnLθ=vi−v∑P(v)vi∂bj∂lnLθ=P(hj=1∣v)−v∑P(v)P(hj=1∣v)
2.3.3、优化求解
Hinton提出了高效的训练RBM的算法——对比散度(Contrastive Divergence, CD)算法。
k步CD算法的具体步骤为:
对 ∀ v \forall v ∀v,取初始值: v ( 0 ) : = v v^{(0)}:=v v(0):=v,然后执行k步Gibbs采样,其中第t步先后执行:
-
利用 P ( h ∣ v ( t − 1 ) ) P ( h ∣ v ( t − 1 ) ) P(h\mid v^{(t−1)})P(h\mid v^{(t−1)}) P(h∣v(t−1))P(h∣v(t−1))采样出 h ( t − 1 ) h^{(t−1)} h(t−1)
-
利用 P ( v ∣ h ( t − 1 ) ) P ( v ∣ h ( t − 1 ) ) P(v\mid h^{(t−1)})P(v\mid h^{(t−1)}) P(v∣h(t−1))P(v∣h(t−1))采样出 v ( t ) v^{(t)} v(t)
上述两个过程分别记为:sample_h_given_v和sample_v_given_h。记 p j v = P ( h j = 1 ∣ v ) , j = 1 , 2 , ⋯ , n h p^v_j=P(h_j=1\mid v),j=1,2,⋯,n_h pjv=P(hj=1∣v),j=1,2,⋯,nh,则sample_h_given_v中的计算可以表示为: -
for j=1,2,⋯,nh do
-
{
- 产生[0,1]上的随机数 r j r_j rj
- h j = { 1 if r j < p j v 0 otherwise h_{j}= \begin{cases}1 & \text { if } r_{j}<p_{j}^{\mathbf{v}} \\ 0 & \text { otherwise }\end{cases} hj={10 if rj<pjv otherwise
-
}
同样,对于sample_v_given_h,记 p i h = P ( v i = 1 ∣ h ) , i = 1 , 2 , ⋯ , n v p^h_i=P(v_i=1\mid h),i=1,2,⋯,n_v pih=P(vi=1∣h),i=1,2,⋯,nv,则sample_h_given_v中的计算可以表示为:
- for j=1,2,⋯,n_h do
- {
- 产生[0,1]上的随机数 r j r_j rj
- v i = { 1 if r i < p i i 0 otherwise v_{i}= \begin{cases}1 & \text { if } r_{i}<p_{i}^{\mathbf{i}} \\ 0 & \text { otherwise }\end{cases} vi={10 if ri<pii otherwise
- }
三、Codes
# import matplotlib.pylab as plt
import numpy as np
# import random
import matplotlib.pyplot as plt
# 导入数据
path = 'mnist.npz'
f = np.load(path)
train_images, train_labels = f['x_train'], f['y_train']
test_images, test_labels = f['x_test'], f['y_test']
x_train_origin,t_train_origin = train_images, train_labels
x_test_origin,t_test_origin = test_images, test_labels
f.close()# (x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
X_train = x_train_origin/255.0
X_test = x_test_origin/255.0
m,h,w = x_train_origin.shape
X_train = X_train.reshape((m,1,h,w))
data = X_train[:5000].reshape(5000,784)
# 定义RBM类class RBM:'''设计一个专用于MNIST生成的RBM模型'''def __init__(self):self.nv = 784self.nh = 500self.lr = 0.1self.W = np.random.randn(self.nh,self.nv)*0.1self.bv = np.zeros(self.nv)self.bh = np.zeros(self.nh)def sigmoid(self,z):return 1.0/(1.0+np.exp(-z))def forword(self,inpt):z = np.dot(inpt,self.W.T) + self.bhreturn self.sigmoid(z)def backward(self,inpt):z = np.dot(inpt,self.W) + self.bvreturn self.sigmoid(z) def train_loader(self, X_train):# 将批次的数据放入self.batchesnp.random.shuffle(X_train)self.batches = []for i in range(0,len(X_train),self.batch_sz):self.batches.append(X_train[i:i+self.batch_sz])self.indice = 0def get_batch(self):if self.indice>=len(self.batches):return Noneself.indice += 1return np.array(self.batches[self.indice-1])def fit(self, X_train, epochs=50, batch_sz = 128):'''用梯度上升法做训练'''self.batch_sz = batch_szerr_list = []for epoch in range(epochs):#初始化data loaderself.train_loader(X_train)err_sum = 0while 1:# 获取每一个批次的数据v0_prob = self.get_batch()# 判断停止条件if type(v0_prob)==type(None):breaksize = len(v0_prob)# 初始化数据dW = np.zeros_like(self.W)dbv = np.zeros_like(self.bv)dbh = np.zeros_like(self.bh)#for v0_prob in batch_data:# 前向计算h0_prob = self.forword(v0_prob) h0 = np.zeros_like(h0_prob)h0[h0_prob > np.random.random(h0_prob.shape)] = 1# 反向计算v1_prob = self.backward(h0)v1 = np.zeros_like(v1_prob)v1[v1_prob > np.random.random(v1_prob.shape)] = 1# 前向计算h1_prob = self.forword(v1)h1 = np.zeros_like(h1_prob) h1[h1_prob > np.random.random(h1_prob.shape)] = 1# 更新权重和偏置dW = np.dot(h0.T , v0_prob) - np.dot(h1.T , v1_prob)dbv = np.sum(v0_prob - v1_prob,axis = 0)dbh = np.sum(h0_prob - h1_prob,axis = 0)# 计算通过RBM计算的数据 v1_prob 和原始的数据 v0_prob 的差距(平均值)err_sum += np.mean(np.sum((v0_prob - v1_prob)**2,axis=1))# 因为是一个批次的计算,所以要除以批次的长度dW /= sizedbv /= sizedbh /= sizeself.W += dW*self.lrself.bv += dbv*self.lrself.bh += dbh*self.lrerr_sum = err_sum / len(X_train)err_list.append(err_sum)print('Epoch {0},err_sum {1}'.format(epoch, err_sum))plt.plot(err_list)def predict(self,input_x):# 前向计算h0_prob = self.forword(input_x) h0 = np.zeros_like(h0_prob)# 抽样h0[h0_prob > np.random.random(h0_prob.shape)] = 1# 反向重建v1 = self.backward(h0)return v1
# 训练模型
rbm = RBM()
rbm.fit(data,epochs=30)
Epoch 0,err_sum 0.3226145231436522
Epoch 1,err_sum 0.1894215878352615
Epoch 2,err_sum 0.1603149519658396
Epoch 3,err_sum 0.14455416861531484
Epoch 4,err_sum 0.1327990997451072
Epoch 5,err_sum 0.12590473771415872
Epoch 6,err_sum 0.11899274631075996
Epoch 7,err_sum 0.11418312942830691
Epoch 8,err_sum 0.1103784907015621
Epoch 9,err_sum 0.10724277163880112
Epoch 10,err_sum 0.1045853946343495
Epoch 11,err_sum 0.10208084398765771
Epoch 12,err_sum 0.09958932872645758
Epoch 13,err_sum 0.09786572348900954
Epoch 14,err_sum 0.09620250876747143
Epoch 15,err_sum 0.09472879435816595
Epoch 16,err_sum 0.09306643274063546
Epoch 17,err_sum 0.09104791313409315
Epoch 18,err_sum 0.09089877918606573
Epoch 19,err_sum 0.08939959546191861
Epoch 20,err_sum 0.0881565612194433
Epoch 21,err_sum 0.0875070280641069
Epoch 22,err_sum 0.08600029603963232
Epoch 23,err_sum 0.08502847499916892
Epoch 24,err_sum 0.08427697958008522
Epoch 25,err_sum 0.0843718926237028
Epoch 26,err_sum 0.08366332665468071
Epoch 27,err_sum 0.08363968930822757
Epoch 28,err_sum 0.08215656937123944
Epoch 29,err_sum 0.08153711678040095
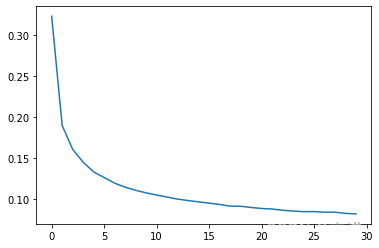
def visualize(input_x):plt.figure(figsize=(5,5), dpi=180)for i in range(0,8):for j in range(0,8):img = input_x[i*8+j].reshape(28,28)plt.subplot(8,8,i*8+j+1)plt.imshow(img ,cmap = plt.cm.gray)
#显示64张手写数字
images = data[0:64]
visualize(images)

#显示重构的图像
rebuild_value = [rbm.predict(x) for x in images]
visualize(rebuild_value)












![[附源码]java毕业设计校园超市进销存管理系统](https://img-blog.csdnimg.cn/6d03989ba7674d859895e9cef26ca113.png)