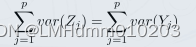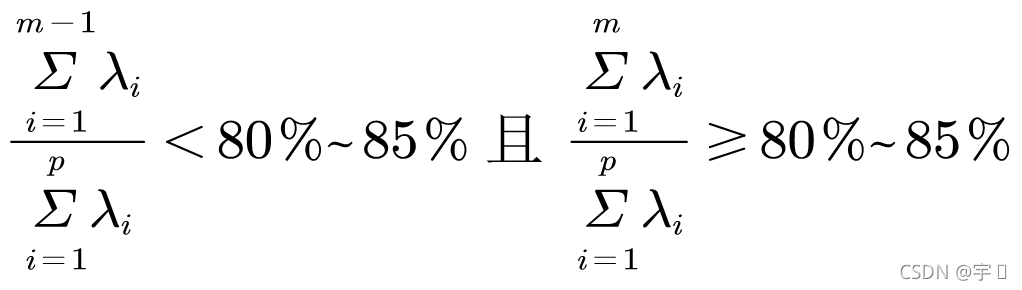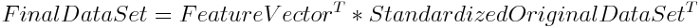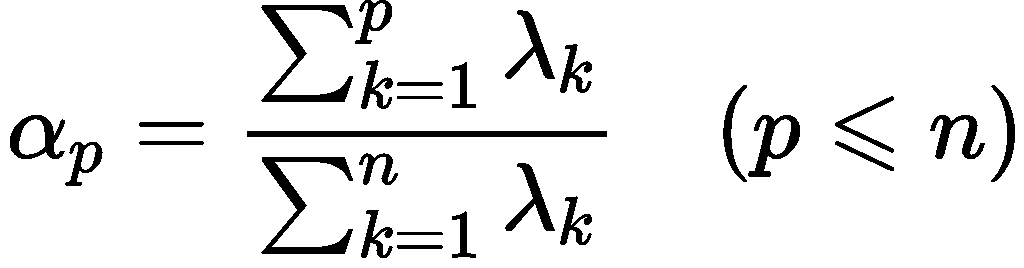主成分分析是用原始变量的线性组合来表示主成分,且主成分彼此之间互不相关,且能反映出原始数据的绝大部分信息。 一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
SPSS 软件中主成分分析与因子分析均在“因子分析”模块中完成。因此,在 SPSS 数据表中录人以上数据后,依次点击“分析-降维-因子”进入“因子分析”对话框,然后将12个变量全部选入“变量”框中。
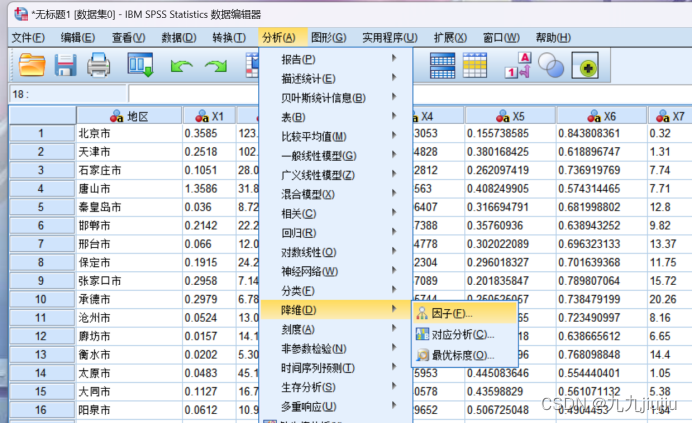
点击右侧的“描述”按钮,在弹出的对话框中,在“相关矩阵”中选择“系数”。点击右侧的“降维”按钮打开相应对话框,其中“方法”是“主成分”,“分析”部分可以选择是从相关阵还是从协方整阵出发求解主成分,默认是从相关阵出发。本例中各变量的量纲差别较大,选择从相关阵出发求解主成分。“显示”部分可以选择输出“未旋转的因子解”和“碎石图”。“降维”部分可以选择提取大于1的特征根与其所对应的主成分或者设定固定的因子(此处为主成分)个数,但是如果选择从协方差阵出发,则会提取大于特征根均值的指定倍数(默认为1)的特征根。点击“确定”运行,即可得到输出结果。
| 表1 相关性矩阵a | ||||||||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | |
| X1 | 1 | 0.244 | 0.18 | 0.807 | -0.023 | -0.009 | 0.023 | 0.107 | -0.118 | -0.359 | 0.097 | -0.155 |
| X2 | 0.244 | 1 | 0.861 | -0.195 | -0.138 | 0.145 | -0.548 | -0.39 | 0.686 | -0.294 | -0.35 | 0.461 |
| X3 | 0.18 | 0.861 | 1 | -0.185 | -0.402 | 0.408 | -0.367 | -0.557 | 0.751 | -0.195 | -0.167 | 0.281 |
| X4 | 0.807 | -0.195 | -0.185 | 1 | 0.027 | -0.067 | 0.318 | 0.179 | -0.351 | -0.403 | 0.176 | -0.277 |
| X5 | -0.023 | -0.138 | -0.402 | 0.027 | 1 | -0.999 | -0.546 | 0.726 | -0.416 | -0.331 | -0.566 | 0.523 |
| X6 | -0.009 | 0.145 | 0.408 | -0.067 | -0.999 | 1 | 0.532 | -0.731 | 0.429 | 0.346 | 0.558 | -0.511 |
| X7 | 0.023 | -0.548 | -0.367 | 0.318 | -0.546 | 0.532 | 1 | -0.253 | -0.299 | 0.357 | 0.523 | -0.728 |
| X8 | 0.107 | -0.39 | -0.557 | 0.179 | 0.726 | -0.731 | -0.253 | 1 | -0.847 | -0.292 | 0.137 | -0.15 |
| X9 | -0.118 | 0.686 | 0.751 | -0.351 | -0.416 | 0.429 | -0.299 | -0.847 | 1 | 0.092 | -0.422 | 0.548 |
| X10 | -0.359 | -0.294 | -0.195 | -0.403 | -0.331 | 0.346 | 0.357 | -0.292 | 0.092 | 1 | 0.131 | -0.217 |
| X11 | 0.097 | -0.35 | -0.167 | 0.176 | -0.566 | 0.558 | 0.523 | 0.137 | -0.422 | 0.131 | 1 | -0.908 |
| X12 | -0.155 | 0.461 | 0.281 | -0.277 | 0.523 | -0.511 | -0.728 | -0.15 | 0.548 | -0.217 | -0.908 | 1 |
| a. 此矩阵不是正定矩阵。 | ||||||||||||
输出结果中,表1是样本相关阵,可以看到12个变量之间部分变量存在较强的相关关系,适合进行主成分分析。
| 表2 总方差解释表 | ||||||
| 成分 | 初始特征值 | 提取载荷平方和 | ||||
| 总计 | 方差百分比 | 累积 % | 总计 | 方差百分比 | 累积 % | |
| 1 | 4.031 | 33.591 | 33.591 | 4.031 | 33.591 | 33.591 |
| 2 | 3.930 | 32.746 | 66.337 | 3.930 | 32.746 | 66.337 |
| 3 | 2.175 | 18.122 | 84.459 | 2.175 | 18.122 | 84.459 |
| 4 | .973 | 8.108 | 92.567 | |||
| 5 | .513 | 4.278 | 96.845 | |||
| 6 | .210 | 1.749 | 98.594 | |||
| 7 | .104 | .864 | 99.458 | |||
| 8 | .041 | .338 | 99.795 | |||
| 9 | .024 | .202 | 99.998 | |||
| 10 | .000 | .002 | 100.000 | |||
| 11 | 5.402E-7 | 4.501E-6 | 100.000 | |||
| 12 | -1.167E-16 | -9.728E-16 | 100.000 | |||
| 提取方法:主成分分析法。 | ||||||
表2给出了相关阵的特征根及对应主成分的方差贡献率和累积贡献率。本例保留了大于1的特征根,可看到提取了3个主成分,其方差贡献率为84.459%,说明该三个主成分基本上提取了原始变量的大部分信息。这样由分析原来的12个变量转化为仅需分析3个综合变量,极大地起到了降维的作用。【注:lamda10、11、12接近于0,意味着中心化以后的原始变量之间存在着多重共线性,即原始变量存在不可忽视的重叠信息】
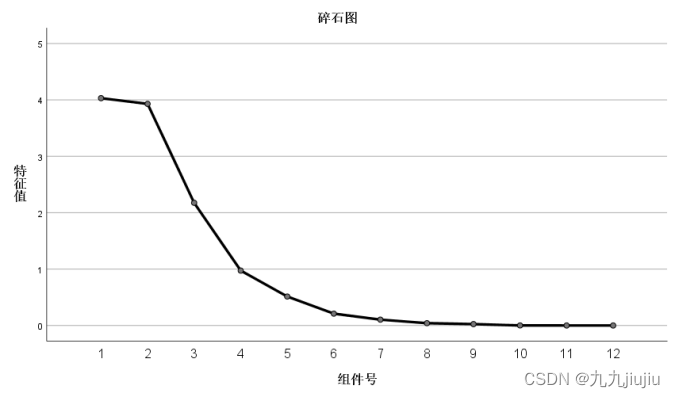
从碎石图中也可以看出,前三个特征根较大,因此选取三个特征根是合适的。
| 表3 成分矩阵a | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | -.102 | -.030 | .908 |
| VAR2 | .836 | .084 | .368 |
| VAR3 | .782 | .353 | .345 |
| VAR4 | -.423 | -.070 | .790 |
| VAR5 | -.032 | -.991 | -.086 |
| VAR6 | .048 | .992 | .055 |
| VAR7 | -.632 | .604 | -.036 |
| VAR8 | -.550 | -.732 | .060 |
| VAR9 | .889 | .390 | -.040 |
| VAR10 | -.132 | .433 | -.646 |
| VAR11 | -.648 | .547 | .141 |
| VAR12 | .773 | -.536 | -.135 |
| 提取方法:主成分分析法。a | |||
| a. 提取了 3 个成分。 | |||
表3是因子载荷阵,需要将其每个元素除以响应主成分的特征根的平方根,才可以得到第一主成分关于标准化的原始变量的变换系数,如表4所示。
| 表4 成分得分系数矩阵 | |||
| 成分 | |||
| 1 | 2 | 3 | |
| VAR1 | -.025 | -.008 | .418 |
| VAR2 | .208 | .021 | .169 |
| VAR3 | .208 | .090 | .159 |
| VAR4 | -.105 | -.018 | .363 |
| VAR5 | -.008 | -.252 | -.040 |
| VAR6 | .012 | .252 | .025 |
| VAR7 | -.157 | .154 | -.016 |
| VAR8 | -.136 | -.186 | .028 |
| VAR9 | .221 | .099 | -.018 |
| VAR10 | -.033 | .110 | -.297 |
| VAR11 | -.161 | .139 | .065 |
| VAR12 | .192 | -.136 | -.062 |
由此可得,主成分Y关于各标准化变量的线性组合为:
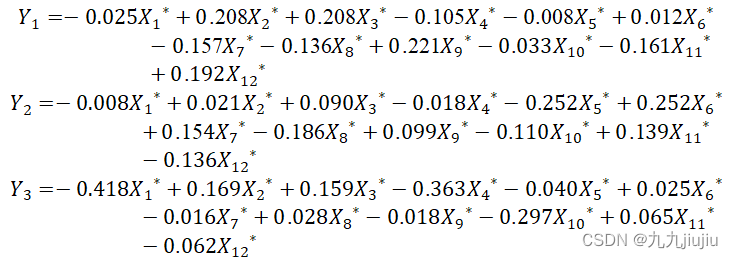
式中各变量的系数的大小可以表示其重要性。
本例中有12个指标,通过主成分计算后,选择了3个主成分。其中,第一主成分的线性组合表达式中X2、X3、X7、X9、X11、X12的系数相对较大,因此第一主成分可看成X2、X3、X7、X9、X11、X12的综合变量,可以理解为第一主成分主要体现了第二、三产业从业人员数、第一、三产业产出结构、第二、三产业劳动生产率,大致反映了产业结构合理化情况;同理,第二主成分可看成X5、X6、X8的综合变量,可以理解为第二主成分主要体现了第二、三产业就业结构及第二产业产出结构,大致反映了产业结构升级化情况;第三主成分可看成X1、X4、X10的综合变量,可以理解为第三主成分主要体现了第一产业从业人员数、产业就业结构及产业劳动生产率,大致反映了产业结构合理化情况。
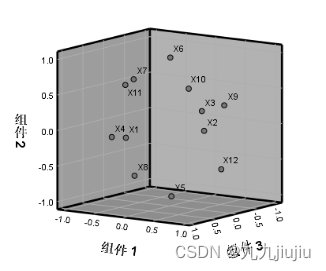
通常为了分析各样品在主成分上所反映的经济意义方面的情况,还需将原始数据代入主成分表达式计算出各样品的主成分得分,根据各样品的主成分得分就可以对样品进行大致分类或者排序。
表5 主成分1的样品排序
| 排序 | 地区 | Y1 | 排序 | 地区 | Y1 |
| 1 | 北京市 | 180.5150607 | 13 | 临汾市 | 10.46116696 |
| 2 | 天津市 | 64.58425815 | 14 | 阳泉市 | 9.58268787 |
| 3 | 太原市 | 28.6908458 | 15 | 运城市 | 9.576200993 |
| 4 | 石家庄市 | 27.51126238 | 16 | 朔州市 | 9.403504998 |
| 5 | 保定市 | 20.44835652 | 17 | 晋中市 | 9.333657238 |
| 6 | 唐山市 | 16.13782061 | 18 | 晋城市 | 8.618180294 |
| 7 | 邯郸市 | 14.34404851 | 19 | 邢台市 | 8.55713213 |
| 8 | 大同市 | 14.18527824 | 20 | 秦皇岛市 | 8.001142876 |
| 9 | 张家口市 | 12.49250853 | 21 | 承德市 | 7.456756398 |
| 10 | 沧州市 | 12.13317336 | 22 | 忻州市 | 7.275499933 |
| 11 | 长治市 | 10.97995128 | 23 | 吕梁市 | 5.205538483 |
| 12 | 廊坊市 | 10.5379542 | 24 | 衡水市 | 4.263760211 |
表6 主成分2的样品排序
| 排序 | 地区 | Y2 | 排序 | 地区 | Y2 |
| 1 | 北京市 | 68.95036761 | 13 | 承德市 | 5.738359679 |
| 2 | 廊坊市 | 21.7017499 | 14 | 晋中市 | 5.250730169 |
| 3 | 衡水市 | 21.32785977 | 15 | 邯郸市 | 5.050358973 |
| 4 | 天津市 | 18.6740728 | 16 | 临汾市 | 4.428244365 |
| 5 | 石家庄市 | 17.85848122 | 17 | 大同市 | 3.900698174 |
| 6 | 秦皇岛市 | 14.01048574 | 18 | 忻州市 | 2.923556626 |
| 7 | 保定市 | 11.93600734 | 19 | 朔州市 | 0.677891108 |
| 8 | 邢台市 | 11.26217305 | 20 | 唐山市 | 0.675547677 |
| 9 | 沧州市 | 10.72374997 | 21 | 长治市 | -1.095271353 |
| 10 | 运城市 | 9.121019677 | 22 | 阳泉市 | -1.189746842 |
| 11 | 太原市 | 7.647849868 | 23 | 吕梁市 | -1.534529357 |
| 12 | 张家口市 | 7.563284738 | 24 | 晋城市 | -1.951322435 |
表7 主成分3的样品排序
| 排序 | 地区 | Y3 | 排序 | 地区 | Y3 |
| 1 | 北京市 | 124.0088998 | 13 | 吕梁市 | -1.403670484 |
| 2 | 天津市 | 39.57507582 | 14 | 保定市 | -1.740401389 |
| 3 | 唐山市 | 12.41857457 | 15 | 临汾市 | -3.664946889 |
| 4 | 太原市 | 9.96648314 | 16 | 忻州市 | -3.96973901 |
| 5 | 长治市 | 4.219456963 | 17 | 石家庄市 | -6.378107088 |
| 6 | 晋城市 | 2.40563238 | 18 | 晋中市 | -7.704121015 |
| 7 | 阳泉市 | 2.125268721 | 19 | 运城市 | -9.152635185 |
| 8 | 邯郸市 | 2.007346431 | 20 | 沧州市 | -14.18356557 |
| 9 | 朔州市 | 1.315259427 | 21 | 邢台市 | -17.43441436 |
| 10 | 大同市 | 0.76826382 | 22 | 秦皇岛市 | -24.86005785 |
| 11 | 张家口市 | -0.194855256 | 23 | 廊坊市 | -43.0706488 |
| 12 | 承德市 | -1.191899812 | 24 | 衡水市 | -45.14251758 |
注意表中各地区得分中,有许多地区的得分是负数,但并不表明这些地区的指标为负,这里的正负仅表示该地区与平均水平的位置关系。