主成分分析思想 核心思路
总体主成分推导
基于标准化变量的总体主成分分析
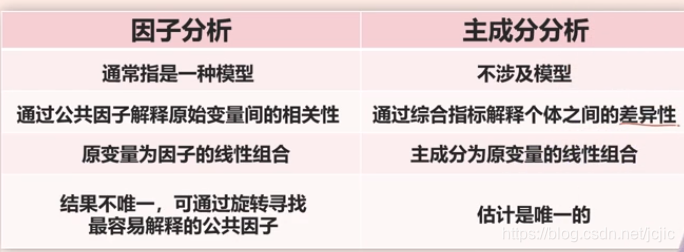
主成分分析(PCA)就是在所有可能的Y1,...,Yn的线性组合模式中,寻找一个或几个(通常小于n个)可以最大程度区分变量的线性组合/加权平均。即期望能将手中许多相关性很高的变量转化成相互独立的变量,并能解释大部分资料之变异的几个新变量,也就是所谓的主成分。
总体主成分分析推导
记原始变量 y=(Y1,......,Yp)’ ,其协方差矩阵为
主成分分析试图定义一组互不相关的变量,称为Y1,........Yp的主成分(PC),记为Z1,......Zp,每一主成分都是Y1,。。。。Yp的线性组合:

则Z1,......,Zp的方差与协方差为
 求解主成分Z1,.......,Zp即求解a1,。。。。,ap
求解主成分Z1,.......,Zp即求解a1,。。。。,ap
主成分(PC)Z1,........,Zp按照”方差贡献度“依次导出:
第一主成分Z1=a1‘y:在满足限制a1’a1=1时,最大化方差var(a‘y)
第二主成分Z2=a2’y:在满足限制a2'a2=1,且cov(a1‘y,a2’y)=0时,最大化方差var(a2‘y)
第j主成分Zj=aj'y:在满足限制aj’aj=1,且cov(ak‘y,aj’y)=0,k<j时,最大化方差var(aj‘y)
主成分(PC)Z1,.....,Zp按照“方差贡献度”依次导出:
第p主成分Zj=a‘y:在满足限制ap’ap=1时,最小化方差var(ap‘y)
定理:
记(1,e1),。。。。(
p,ep)为协方差矩阵
的特征值-特征向量,
1>
2≥。。。。≥
p≥0并且特征向量e1, 。。。。ep是正交化特征向量。
则变量Y1,.....,Yp的第j个主成分由下式给出:
Zj=ej’y=ej1Y1+ej2Y2+ +ejpYp,j=1,.....,p,
这里有var(Zj)=ej‘ej=
j
并且有cov(Zj,Zk)=ej‘ek=0
进一步地,我们有:![]()
基于标准化变量的总体主成分分析:
当变量y=(Y1,....,Yp)‘的数值(由于度量单位不同等原因)差距过大,直接由协方差矩阵生成的主成分会由方差大的变量主导。
在这种情况下,我们对每一个变量Yj做标准化,等价于基于原变量Y1,....Yp的相关系数矩阵进行主成分分析。
主成分分析案例:
| 地区 | 经营单位所在地进出口总额/103美元 | 全社会固定资产投资利用外资/亿元 | 城镇单位在岗职工平均工资/元 | 社会消费品零售总额/亿元 | 医疗卫生机构数/个 | 普通高等学校在校学生数/万人 | 城镇居民人均可支配收入/元 | 农村居民人均可支配收入/元 | 地方财政一般预算收入/亿元 | 城镇单位就业人员/万人 | 地区生产总值/亿元 | 第三产业增加值/亿元 | 全社会固定资产投资/亿元 | 人均地区生产总值/(元/人) | 外商及港澳台商投资工业企业利润总额/亿元 |
| 北京市 | 324017423 | 21.53 | 134994 | 11575.4 | 9976 | 59.29 | 62406.3 | 24240.5 | 5430.79 | 812.86 | 28014.94 | 22567.76 | 8370.44 | 128994 | 776.84 |
| 天津市 | 112919165 | 32.02 | 96965 | 5729.7 | 5539 | 51.47 | 40277.5 | 21753.7 | 2310.36 | 269.48 | 18549.19 | 10786.64 | 11288.92 | 118944 | 461.66 |
| 河北省 | 49855543 | 74.71 | 65255 | 15907.6 | 80912 | 126.89 | 30547.8 | 12880.9 | 3233.83 | 535.32 | 34016.32 | 15040.13 | 33406.8 | 45387 | 401.76 |
| 山西省 | 17186875 | 9.17 | 61547 | 6918.1 | 42490 | 76.3 | 29131.8 | 10787.5 | 1867 | 428.68 | 15528.42 | 8030.37 | 6040.54 | 42060 | 134.43 |
| 内蒙古 | 13873523 | 3.5 | 67688 | 7160.2 | 24218 | 44.81 | 35670 | 12584.3 | 1703.21 | 280.63 | 16096.21 | 8046.76 | 14013.16 | 63764 | 135.58 |
| 辽宁省 | 99595084 | 191.93 | 62545 | 13807.2 | 35767 | 98.1 | 34993.4 | 13746.8 | 2392.77 | 519.48 | 23409.24 | 12307.16 | 6676.74 | 53527 | 583.66 |
代码:
> library(psych) 利用psych包做主成分分析
> library(tidyverse) 用于数据加载及预处理
> library(xlsx) 用xlsx包读取数据
> d<-read.xlsx("E:/R/shuju/shuju4.xlsx",1) 用read.xlsx()函数读取数据
> nms<-d[['地区']] 保存地区名称
> d<-d[,-1] 去掉第一列(地区名称)
> d<-data.frame(d) 将数据转化为数据框
> d<-scale(x=d) 数据标准化
> fa.parallel(d,fa='pc') 绘制碎石图
> p<-principal(d,nfactors=2,rotate="none") 提取主成分
> p$values 特征根
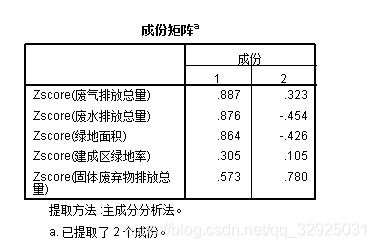
> p$loadings 主成分载荷矩阵
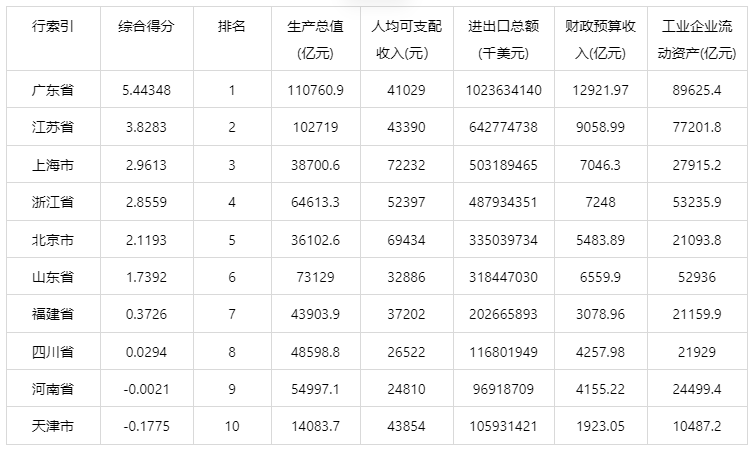
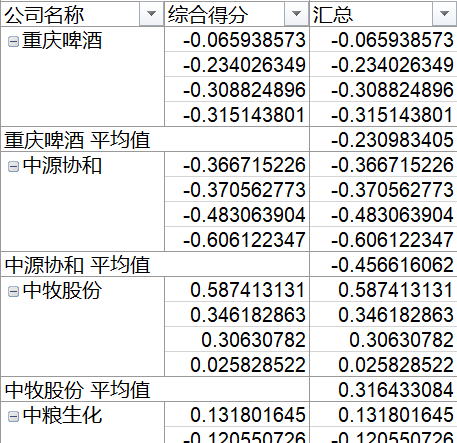
> p$scores 主成分得分
-