一、说明
这篇文章的目的是提供主成分分析(PCA)的完整和简化的解释。我们将逐步介绍它是如何工作的,这样每个人都可以理解并使用它,即使是那些没有强大数学背景的人。
PCA是网络上广泛覆盖的机器学习方法,并且有一些关于它的很棒的文章,但是许多人在这个主题上花费了太多时间,而我们大多数人只是想知道它是如何以简化的方式工作的。
主成分分析可以分为五个步骤。我将介绍每个步骤,提供PCA正在做什么的逻辑解释,并简化数学概念,如标准化,协方差,特征向量和特征值,而不关注如何计算它们。
二、如何进行主成分分析?
- 标准化连续初始变量的范围
- 计算协方差矩阵以识别相关性
- 计算协方差矩阵的特征向量和特征值以识别主成分
- 创建特征向量以决定要保留哪些主成分
- 沿主分量轴重铸数据
首先,一些基本(和简短)的背景对于上下文是必要的。
三、主成分分析 (PCA) 概述
3.1 什么是主成分分析?
主成分分析(PCA)是一种降维方法,通常用于降低大型数据集的维数,方法是将大型变量集转换为仍包含大型数据集中大部分信息的较小变量集。
减少数据集的变量数量自然是以牺牲准确性为代价的,但降维的诀窍是用一点准确性来换取简单性。因为较小的数据集更容易探索和可视化,并且使机器学习算法的数据点分析更加容易和快捷,而无需处理无关的变量。
因此,总而言之,PCA的想法很简单 - 减少数据集的变量数量,同时保留尽可能多的信息。
3.2 PCA的分步说明
第 1 步:标准化
此步骤的目的是标准化连续初始变量的范围,以便每个变量对分析的贡献相同。
更具体地说,在PCA之前执行标准化至关重要的原因是后者对初始变量的方差非常敏感。也就是说,如果初始变量的范围之间存在较大差异,则范围较大的变量将主导范围较小的变量(例如,范围在 0 到 100 之间的变量将主导范围在 0 到 1 之间的变量),这将导致结果偏差。因此,将数据转换为可比较的比例可以防止此问题。
在数学上,这可以通过减去平均值并除以每个变量的每个值的标准差来完成。
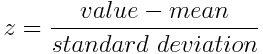
标准化完成后,所有变量都将转换为相同的比例。
第 2 步:协方差矩阵计算
此步骤的目的是了解输入数据集的变量如何与平均值相互变化,或者换句话说,查看它们之间是否存在任何关系。因为有时,变量高度相关,以至于它们包含冗余信息。因此,为了识别这些相关性,我们计算协方差矩阵。
协方差矩阵是一个 p × p 对称矩阵(其中 p 是维数),其条目是与初始变量的所有可能对关联的协方差。例如,对于具有 3 个变量 x、y 和 z 的三维数据集,协方差矩阵是 3×3 的数据矩阵,来自:

由于变量与自身的协方差是其方差(Cov(a,a)=Var(a)),因此在主对角线(从左上到右下)中,我们实际上具有每个初始变量的方差。由于协方差是可交换的(Cov(a,b)=Cov(b,a)),协方差矩阵的条目相对于主对角线是对称的,这意味着上三角形和下三角形部分相等。
我们作为矩阵条目的协方差告诉我们变量之间的相关性是什么?
实际上,协方差的符号很重要:
- 如果为正,则:两个变量一起增加或减少(相关)
- 如果为负,则:一个增加,另一个减少(负相关)
现在我们知道协方差矩阵只不过是一个总结所有可能的变量对之间相关性的表,让我们进入下一步。
步骤 3:计算协方差矩阵的特征向量和特征值以识别主成分
特征向量和特征值是我们需要从协方差矩阵计算以确定数据主成分的线性代数概念。在解释这些概念之前,让我们首先了解主成分的含义。
主成分是构造为初始变量的线性组合或混合的新变量。这些组合的完成方式是,新变量(即主成分)不相关,并且初始变量中的大部分信息被压缩或压缩到第一个分量中。所以,这个想法是 10 维数据给你 10 个主分量,但 PCA 试图在第一个分量中放置最大可能的信息,然后在第二个分量中放置最大剩余信息,依此类推,直到得到下面碎石图所示的东西。
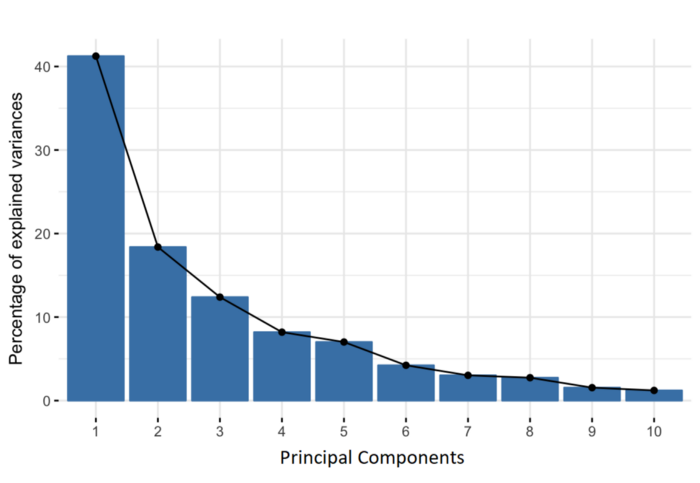
以这种方式组织主组件中的信息将允许您在不丢失太多信息的情况下降低维数,这是通过丢弃信息量低的组件并将剩余组件视为新变量来实现的。
这里要认识到的重要一点是,主成分的可解释性较差,并且没有任何实际意义,因为它们被构造为初始变量的线性组合。
从几何上讲,主成分表示解释最大方差量的数据方向,即捕获数据大部分信息的线。这里的方差和信息之间的关系是,一条线携带的方差越大,沿它的数据点的离散度就越大,沿一条线的离差越大,它拥有的信息就越多。简单地说,只需将主分量视为新轴,这些轴提供了查看和评估数据的最佳角度,以便更好地看到观测值之间的差异。
四、PCA 如何构造主成分
由于数据中的变量与变量一样多的主成分,因此主成分的构造方式是,第一个主成分占数据集中最大可能的方差。例如,假设我们数据集的散点图如下所示,我们可以猜出第一个主成分吗?是的,它大约是与紫色标记匹配的线,因为它穿过原点,并且它是点(红点)投影最分散的线。或者从数学上讲,它是最大化方差(从投影点(红点)到原点的平方距离的平均值)的线。
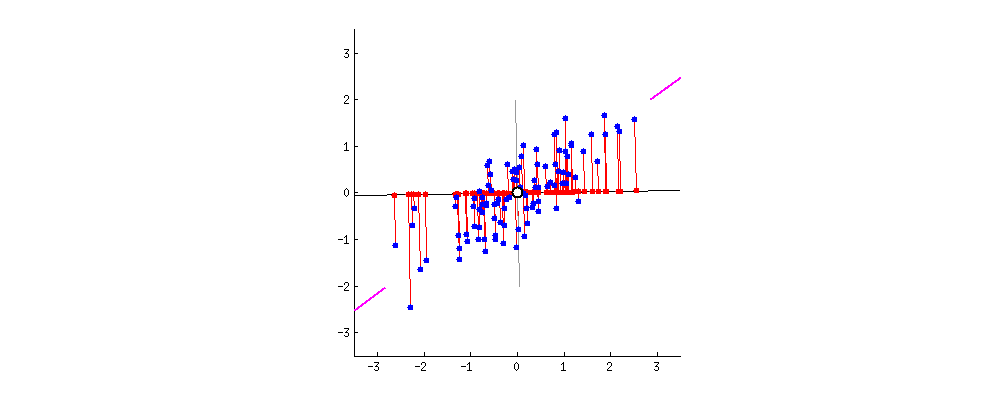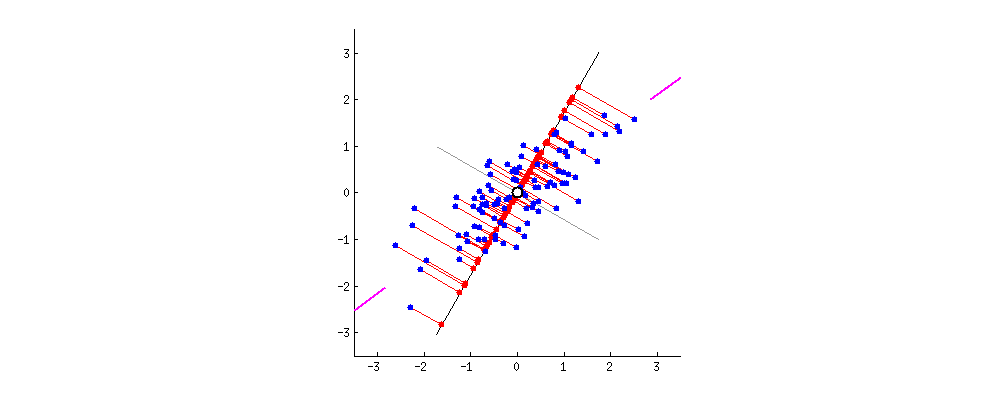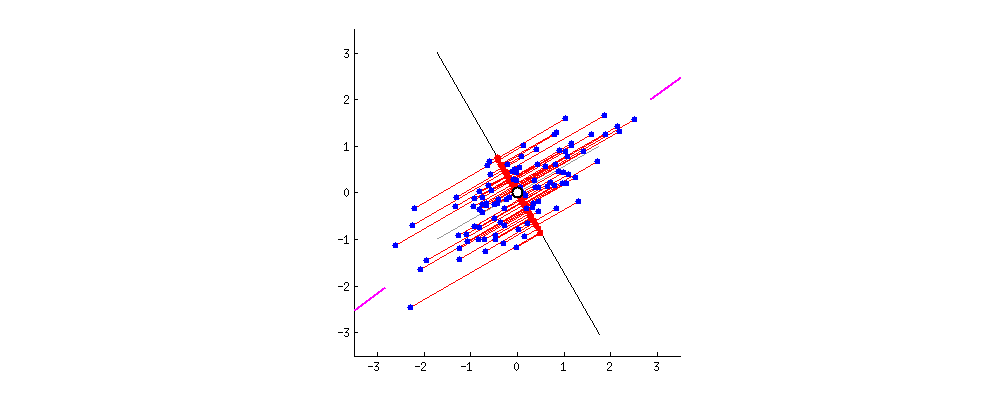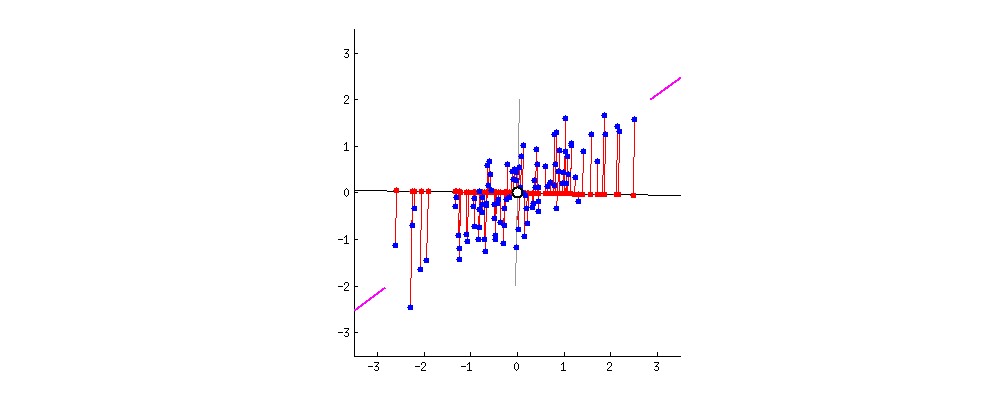
第二个主成分的计算方式相同,条件是它与第一个主成分不相关(即垂直于)第一个主成分,并且它占下一个最高方差。
这一直持续到计算出总共 p 个主成分,等于原始变量数。
现在我们理解了主成分的含义,让我们回到特征向量和特征值。您首先需要了解的是它们总是成对出现,因此每个特征向量都有一个特征值。它们的数量等于数据的维度数。例如,对于三维数据集,有 3 个变量,因此有 3 个特征向量和 3 个相应的特征值。
事不宜迟,特征向量和特征值是上述所有魔力的幕后推手,因为协方差矩阵的特征向量实际上是方差最大(信息最多)的轴的方向,我们称之为主分量。特征值只是附加到特征向量的系数,它给出了每个主成分中携带的方差量。
通过按特征值从高到低的顺序对特征向量进行排序,您可以按显著性顺序获得主分量。
4.1 主成分分析示例:
假设我们的数据集是二维的,有 2 个变量 x,y,协方差矩阵的特征向量和特征值如下:
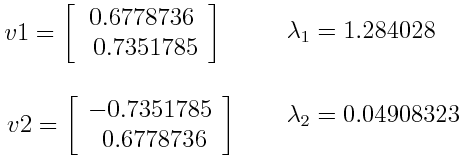
如果我们按降序对特征值进行排名,我们得到 λ1>λ2,这意味着对应于第一个主成分 (PC1) 的特征向量是 v1,对应于第二个主成分 (PC2) 的特征向量是v2。
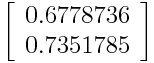
在获得主分量后,为了计算每个分量所占的方差(信息)的百分比,我们将每个分量的特征值除以特征值的总和。如果我们在上面的例子上应用它,我们发现 PC1 和 PC2 分别承载了 96% 和 4% 的数据方差。
第 4 步:特征向量
正如我们在上一步中看到的,计算特征向量并按其特征值降序对它们进行排序,使我们能够按显著性顺序找到主分量。在此步骤中,我们要做的是选择是保留所有这些分量还是丢弃那些重要性较低的分量(低特征值),并与剩余的分量形成一个我们称之为特征向量的向量矩阵。
因此,特征向量只是一个矩阵,它将我们决定保留的组件的特征向量作为列。这使其成为降维的第一步,因为如果我们选择仅将 p 特征向量(分量)排除在 n 之外,则最终数据集将只有 p 维。
4.2 主成分分析示例:
继续上一步中的示例,我们可以同时使用特征向量 v1 和 v2 形成一个特征向量:

或者丢弃特征向量 v 2,这是重要性较小的特征向量,并仅形成 v1 的特征向量:
丢弃特征向量 v2 会将维数降低 1,从而导致最终数据集中的信息丢失。但鉴于 v 2 只携带了 4% 的信息,因此损失并不重要,我们仍将拥有 v96 携带的 1% 的信息。
因此,正如我们在示例中所看到的,您可以选择是保留所有组件还是丢弃重要性较低的组件,具体取决于您要查找的内容。因为如果您只想根据不相关的新变量(主成分)来描述数据,而不寻求降低维度,则不需要省略不太重要的组件。
步骤 5:沿主分量轴重新转换数据
在前面的步骤中,除了标准化之外,您不会对数据进行任何更改,只需选择主成分并形成特征向量,但输入数据集始终保持原始轴(即初始变量)。
在此步骤(即最后一步)中,目的是使用使用协方差矩阵的特征向量形成的特征向量,将数据从原始轴重新定向到主分量表示的轴(因此称为主分量分析)。这可以通过将原始数据集的转置乘以特征向量的转置来完成。
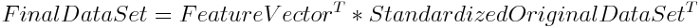
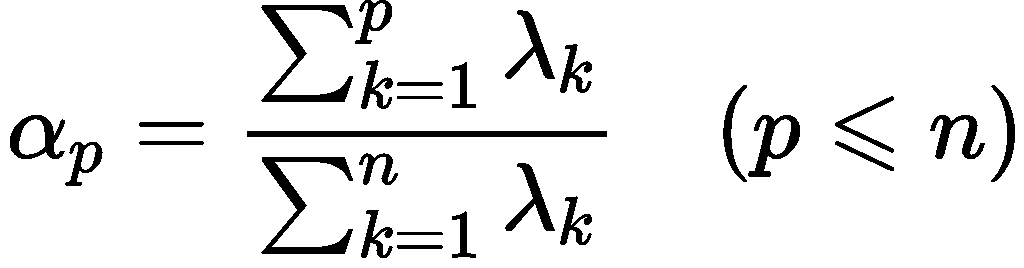





![[将小白进行到底] 如何比较两篇文章的相似度](https://images0.cnblogs.com/blog/79263/201304/02151548-f7e8409392c846498b9d9e548e92926f.png)