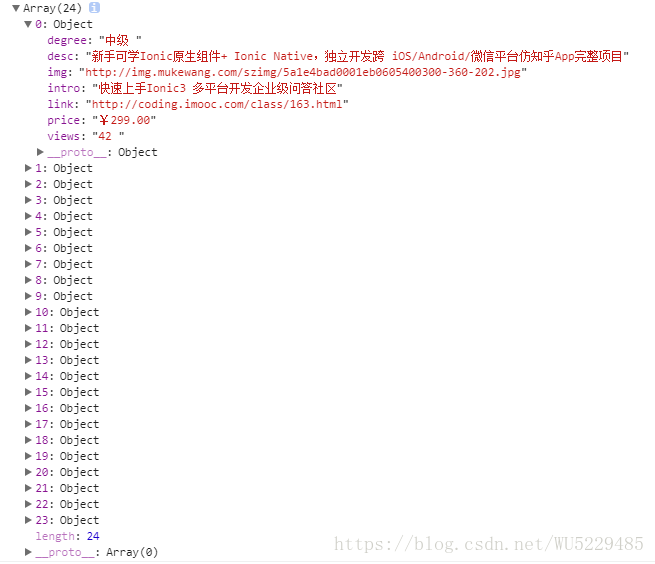
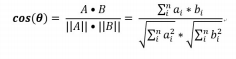去百度文库上一搜,是很老的题目了。这里所做的只是准备工作,为后面更多的数据处理做准备。
例题
1.对原始资料矩阵进行标准化处理
zef_data = xlsread('chengshi.xls');
z = zscore(zef_data)z =1.1977 0.7149 0.6674 1.1390 0.9189 3.1113 2.5079 3.2677 3.6461 3.60180.5570 0.6125 0.3058 1.3990 -0.6652 1.3427 0.5439 0.7769 1.1365 0.83940.4914 -1.4940 1.8031 -0.1495 -0.6958 -0.9003 -0.3724 0.1012 -0.1547 -0.3345-0.5940 1.0693 -1.0304 -0.5571 -0.7879 0.0172 -0.5484 -0.4053 -0.2385 -0.4168-0.7678 -0.2339 -0.8938 -0.7459 -0.7494 -0.8349 -0.6636 -0.8144 -0.7997 -0.68730.1174 0.9093 0.0886 -0.2536 -0.2453 0.3405 -0.1177 0.4098 0.3259 -0.0252-0.1312 0.0896 0.7057 0.0019 0.0330 0.6874 0.0492 0.1752 -0.1721 -0.17190.1440 -0.4423 0.6777 -0.2398 -0.5212 -0.1999 -0.3668 -0.2671 -0.0699 -0.23590.5889 -0.1036 1.5339 -0.4148 -0.3439 -0.3848 -0.2199 -0.0026 0.7761 0.09751.3169 1.5667 0.9057 4.5318 -0.3730 3.0124 4.3123 3.1335 2.7543 3.4700-0.1460 0.3290 -0.2349 0.4584 0.3569 -0.0473 -0.0039 -0.1262 0.0649 0.13570.0022 -0.7525 0.2146 0.3531 0.6924 -0.0022 -0.2575 0.1542 -0.1390 -0.0032-0.1442 -1.3638 0.2288 0.2177 1.0945 -0.1295 -0.1959 -0.1960 -0.5580 -0.2833-0.3487 -0.9778 -0.6156 -0.5790 -0.5135 -0.9365 -0.5126 -0.7781 -0.7374 -0.6401-0.0598 -1.2511 0.9936 -0.1820 -0.1461 -0.4152 -0.2363 -0.2307 -0.4683 -0.3959-0.9164 0.0406 -0.9276 -0.2610 -0.6216 -0.8398 -0.2939 -0.7001 -0.7415 -0.4141-0.3596 -0.4907 -0.5527 -0.5995 -0.6266 -0.7829 -0.5905 -0.6146 -0.5589 -0.5537-0.1079 -0.4320 0.2902 -0.2084 -0.4186 0.0062 -0.2444 -0.3758 -0.3029 -0.33620.1662 -0.6695 1.2366 0.3031 0.2770 0.4899 -0.0108 -0.2391 -0.0592 -0.17530.0009 -0.8324 -0.5642 -0.3065 0.0008 -0.4540 -0.3311 -0.2138 -0.2866 -0.38320.2364 0.6488 -0.0003 -0.0886 -0.0586 0.3432 -0.0744 -0.1154 0.4917 0.1019-0.0611 -1.0245 -0.0689 -0.5217 -0.1595 -0.5505 -0.4063 -0.4827 -0.4685 -0.46150.1323 0.8578 0.4110 1.4680 1.0752 1.1163 1.2921 2.2388 0.8969 1.4621-0.9336 1.8981 -0.9632 1.1753 -0.1551 -0.6832 1.3941 0.4906 -0.2070 0.5537-0.6205 -0.4447 -0.5187 -0.7131 -0.4915 -0.7733 -0.6117 -0.6868 -0.7637 -0.6383-1.0571 2.1543 -1.2324 -0.7556 -0.4715 -0.8594 -0.6525 -0.7774 -1.0782 -0.77464.6348 -1.6546 3.1235 0.0175 3.9004 1.2330 0.2732 0.4217 1.3904 0.33110.7331 -0.8773 0.7647 -0.2469 2.7585 0.7283 -0.1257 0.1628 0.2950 0.0123-0.5533 -0.1460 -0.8973 -0.6052 0.4900 -0.6952 -0.5548 -0.7516 -0.6409 -0.6007-0.2668 -0.5653 -0.4417 -0.4718 -0.4475 0.0307 -0.1694 -0.3756 -0.2450 -0.26900.1125 -0.4265 -0.4982 -0.4659 -0.0105 -0.1784 -0.3056 -0.0967 0.0673 -0.2353-0.6172 0.3920 -1.0057 -0.5371 -0.7976 -0.6395 -0.5883 -0.6144 -0.5136 -0.4977-0.9070 0.2599 -1.2102 -0.7562 -0.8056 -0.9410 -0.7305 -0.9014 -0.9793 -0.7581-0.9797 0.5519 -1.0985 -0.7611 -0.7722 -0.9663 -0.7003 -0.9080 -1.0214 -0.7900-0.8599 2.0877 -1.1968 -0.6446 -0.7200 -0.2451 -0.4875 -0.6588 -0.6410 -0.5238
2.计算相关系数矩阵
cor = corrcoef(z)
cor =1.0000 -0.3444 0.8425 0.3603 0.7390 0.6215 0.4039 0.4967 0.6761 0.4689-0.3444 1.0000 -0.4750 0.3096 -0.3539 0.1971 0.3571 0.2600 0.1570 0.30900.8425 -0.4750 1.0000 0.3358 0.5891 0.5056 0.3236 0.4456 0.5575 0.37420.3603 0.3096 0.3358 1.0000 0.1507 0.7664 0.9412 0.8480 0.7320 0.86140.7390 -0.3539 0.5891 0.1507 1.0000 0.4294 0.1971 0.3182 0.3893 0.25950.6215 0.1971 0.5056 0.7664 0.4294 1.0000 0.8316 0.8966 0.9302 0.90270.4039 0.3571 0.3236 0.9412 0.1971 0.8316 1.0000 0.9233 0.8376 0.95270.4967 0.2600 0.4456 0.8480 0.3182 0.8966 0.9233 1.0000 0.9201 0.97310.6761 0.1570 0.5575 0.7320 0.3893 0.9302 0.8376 0.9201 1.0000 0.93960.4689 0.3090 0.3742 0.8614 0.2595 0.9027 0.9527 0.9731 0.9396 1.0000
3.计算该相关系数矩阵的特征值和特征向量,并对特征值进行排序
[vec, val] = eig(cor) %特征向量vec 特征值val
newval = diag(val); %取主对角线上的数值,排成一列数组
newy = sort(newval, 'descend')vec =-0.1367 0.2282 -0.2628 0.1939 0.6371 -0.2163 0.3176 -0.1312 -0.4191 0.2758-0.0329 -0.0217 0.0009 0.0446 -0.1447 -0.4437 0.4058 -0.5562 0.5487 0.0593-0.0522 -0.0280 0.2040 -0.0492 -0.5472 -0.4225 0.3440 0.3188 -0.4438 0.24010.0067 -0.4176 -0.2856 -0.2389 0.1926 -0.4915 -0.4189 0.2726 0.2065 0.34030.0404 -0.1408 0.0896 0.0380 -0.1969 -0.0437 -0.4888 -0.6789 -0.4405 0.1861-0.0343 0.2360 0.0640 -0.8294 0.0377 0.2662 0.1356 -0.1290 0.0278 0.37820.2981 0.4739 0.5685 0.2358 0.1465 -0.1502 -0.2631 0.1245 0.2152 0.36440.1567 0.3464 -0.6485 0.2489 -0.4043 0.2058 -0.0704 0.0462 0.1214 0.38120.4879 -0.5707 0.1217 0.1761 0.0987 0.3550 0.3280 -0.0139 0.0071 0.3832-0.7894 -0.1628 0.1925 0.2510 -0.0422 0.2694 -0.0396 0.0456 0.1668 0.3799val =0.0039 0 0 0 0 0 0 0 0 00 0.0240 0 0 0 0 0 0 0 00 0 0.0307 0 0 0 0 0 0 00 0 0 0.0991 0 0 0 0 0 00 0 0 0 0.1232 0 0 0 0 00 0 0 0 0 0.2566 0 0 0 00 0 0 0 0 0 0.3207 0 0 00 0 0 0 0 0 0 0.5300 0 00 0 0 0 0 0 0 0 2.3514 00 0 0 0 0 0 0 0 0 6.2602newy =6.26022.35140.53000.32070.25660.12320.09910.03070.02400.0039特征值降序排序。
4.确定主成分个数
newrate = newy./sum(newy %求方差贡献率newrate =0.62600.23510.05300.03210.02570.01230.00990.00310.00240.0004
0.6260 + 0.2351 > 0.8,因此留下前两个主成分即可。
5.建立相应主成分方程
确定留下两个主成分,我们把vec最后两列留下,它们是主成分的系数。

其中X1~X10是归一化以后的向量。
由图可得,X9是最重要的变量,其次是X9,再其次是X10。
6.计算主成分得分
sco = z * vec;sco =-0.0891 0.0216 0.2222 0.3641 -0.2957 1.9306 0.5594 -0.4799 1.0743 7.1934-0.0001 -0.3269 -0.3512 -0.6205 0.3922 -0.1147 0.5937 0.4695 0.9456 2.3723-0.0169 0.0433 -0.2005 0.5222 -0.4797 -0.4093 0.5040 1.8343 -1.7000 -0.32440.0494 0.0214 -0.1218 -0.3047 0.1567 0.2042 0.6227 -0.5672 1.2869 -1.2816-0.0202 0.0466 0.0328 0.0544 0.1884 0.2876 -0.0839 0.2186 0.3809 -2.26910.1342 0.1297 -0.2376 -0.0469 -0.2427 -0.0294 0.8191 -0.4409 0.4981 0.33290.0498 0.3153 0.0852 -0.6438 -0.5363 -0.2077 0.2389 0.0905 -0.2021 0.3587-0.0553 -0.0382 0.0198 -0.0463 -0.1089 -0.1221 0.5292 0.6896 -0.5805 -0.42980.0751 -0.3394 0.2110 0.5479 -0.4345 -0.2788 1.2710 0.6056 -0.9551 0.42720.0139 0.1042 0.1283 -0.1621 0.6668 -0.8618 -0.5308 1.1461 2.9966 8.4253-0.0559 -0.3915 0.0024 -0.0457 0.0553 -0.2344 -0.3407 -0.3509 0.2890 0.1543-0.0743 -0.2234 -0.2604 -0.1475 -0.1892 0.0586 -0.7060 0.0900 -0.7793 0.1662-0.0350 -0.0815 0.0042 -0.2673 -0.1908 0.0650 -1.2707 0.1448 -1.3473 -0.3044-0.0097 0.0646 0.0248 0.2097 0.4041 0.3097 -0.3798 0.5863 -0.3534 -1.9579-0.0179 0.1240 0.1116 -0.0290 -0.3936 -0.1514 -0.1531 1.0720 -1.2353 -0.6021-0.0579 -0.0769 0.1336 0.1270 0.1426 0.0293 -0.3946 0.1837 0.7919 -1.8106-0.0161 0.0143 -0.0655 0.1748 0.2529 0.2573 -0.0151 0.3875 -0.0409 -1.7517-0.0188 0.1056 0.1127 -0.3146 -0.0221 -0.0239 0.1877 0.5146 -0.3355 -0.6083-0.0000 -0.0579 0.2855 -0.6432 -0.3549 -0.4078 0.0178 0.5566 -1.0925 0.45870.1007 0.0498 -0.2158 0.1627 0.3793 0.4381 -0.4419 0.1929 -0.4462 -0.91790.0508 -0.2062 0.0924 -0.1250 0.1443 -0.0120 0.6355 -0.4374 0.2646 0.3484-0.0064 0.1034 0.0367 0.1067 0.1661 0.2847 -0.2316 0.5056 -0.7851 -1.1965-0.0335 0.1369 -0.5282 0.1946 -0.8407 -0.0752 -0.7187 -0.5187 0.8937 3.53130.0949 0.0011 0.2132 0.7842 -0.1493 -1.0186 -0.8578 -0.5021 2.6027 0.5625-0.0302 0.0791 0.0487 0.0686 0.0228 0.2242 -0.1379 0.2761 -0.0330 -1.9686-0.0874 0.0886 -0.0004 0.0955 -0.2510 -0.6968 0.4484 -1.3650 1.8280 -2.3713-0.0626 0.1688 -0.0441 0.2900 0.7580 -0.8106 0.4699 -1.4452 -5.7415 4.04730.0956 -0.1221 0.1880 -0.3089 -0.4433 0.2627 -0.8883 -1.4101 -2.3768 1.17260.0453 -0.1380 0.1128 0.0887 0.1050 0.1939 -0.6115 -0.6625 -0.1256 -1.71690.0393 0.2042 0.1418 -0.2290 0.2662 0.5435 -0.0443 0.3325 -0.0305 -0.84630.1396 0.0244 -0.1590 0.1429 0.3225 0.5438 -0.0141 -0.0874 -0.2729 -0.5537-0.0191 -0.0529 -0.0960 0.0687 0.2623 0.1586 0.1944 -0.0972 0.8548 -1.7961-0.0650 0.0523 -0.0207 0.0664 0.2170 0.1209 -0.0516 -0.1027 0.8322 -2.5616-0.0557 0.0589 0.0345 0.0734 0.0630 -0.0754 0.0445 -0.2381 0.9570 -2.5623-0.0612 0.0966 0.0587 -0.2082 -0.0330 -0.3826 0.7363 -1.1913 1.9373 -1.7202
倒数第一列是第一主成分在35个城市中的得分,倒数第二列是是第二主成分在35个城市中的得分,以此类推。
倒数第一列的重要性是0.6260,倒数第二列的重要性是0.2351。
7.建立排序指标,进行排序
因为所有向量指标都是同向的,可以用如下方式对城市进行排序。
nowsco = sco(:, end) .* newrate(1) + sco(:, end-1) .* newrate(2)
[a,x] = sort(nowsco, 'descend')a =5.97904.75582.42081.70751.18370.96410.32560.28030.17700.17520.16460.04290.0303-0.0792-0.4056-0.4108-0.4597-0.4997-0.5074-0.5370-0.6028-0.6214-0.6674-0.6796-0.9234-0.9336-0.9473-1.0546-1.1043-1.1062-1.2401-1.3088-1.3310-1.3790-1.4079x =1012322724621728119191283118413303351520322216262917251453433光最后两列就占了所有的%86的信息,所以我们以最后两列的主成分得分为排序指标,对城市进行排序。
原本表上所列的第10个城市,综合指标排在第一,原本表上所列的第1个城市,综合指标排在第二,以此类推。
排序完成。
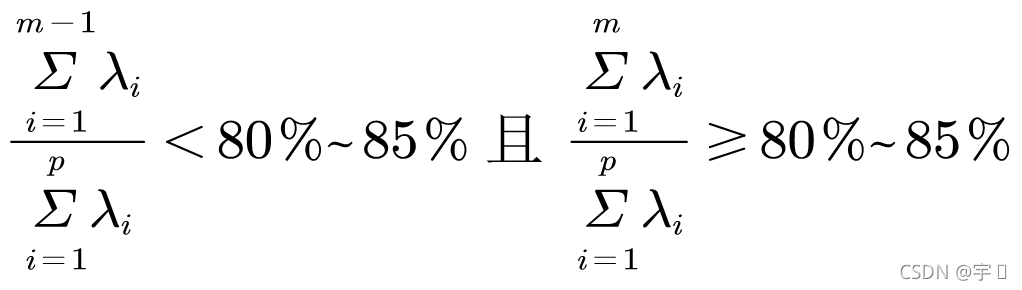
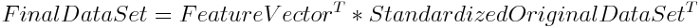
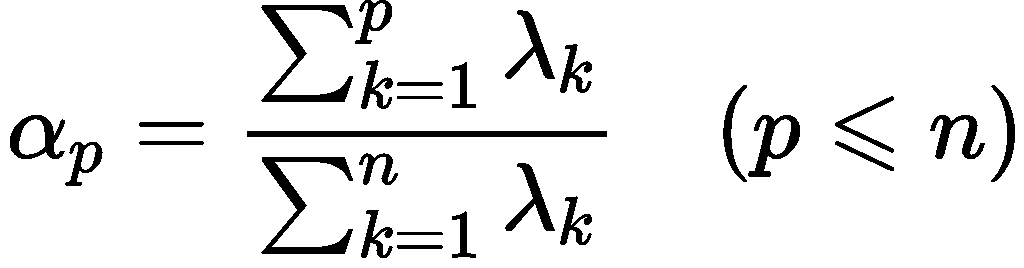





![[将小白进行到底] 如何比较两篇文章的相似度](https://images0.cnblogs.com/blog/79263/201304/02151548-f7e8409392c846498b9d9e548e92926f.png)