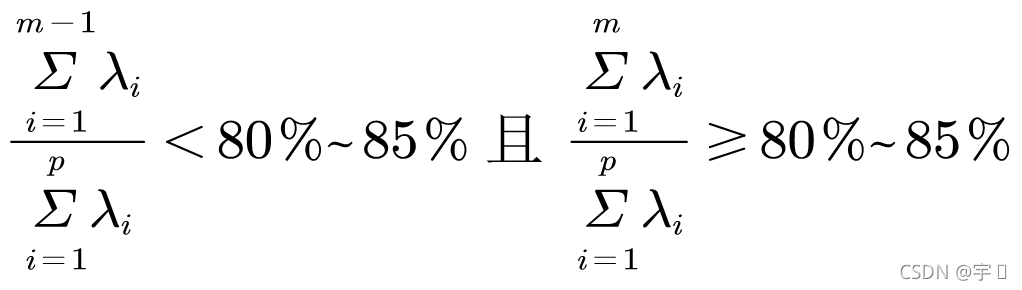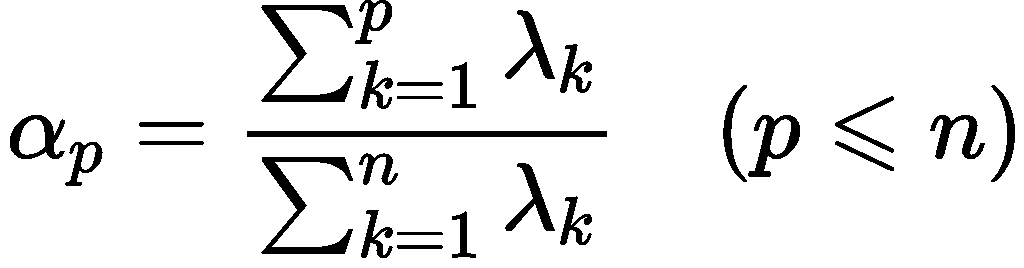* * * *
*
* * *
因子分析是主成分分析的推广和发展,它也是多元统计分析中将为的一种方法. 因子分析是研究相关阵和或协方差阵的内部依赖关系,它将多个变量综合为少数几个因子,以再现原始变量与因子之间的相关关系.
因子分析的思想一般认为始于Charles Spearman 于1904年发表的文章,他提出用这种方法来解决智力测验得分的统计分析. 目前因子分析在心理学、医学、地质学和经济学等领域都取得了成功的应用。

* * * * * *
导航
1 正交因子模型
1.1 模型设定
1.2 模型假设
1.3 模型求解
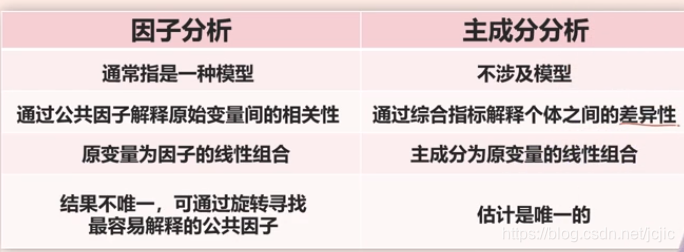
2 因子分析模型与主成分分析模型的联系与区别
3 具体案例
* * * * * *
1 正交因子模型
1.1 模型设定
设有p维列向量
为标准化(Z-score)后原有可观测指标向量. 因子分析希望对于每个变量 ,用m个公共因子
来解释,即
上式用矩阵表示为
, 其中A为(p×m)的矩阵
称 为X的特殊因子,代表了前面m个因子之外剩余因子之和;
为第 i 个变量在第 j 个因子上的载荷.
1.2 模型假设
1.3 模型求解(矩阵的谱分解相关知识可点击参见我的另一篇文章)
相比主成分分析,因子分析更倾向于描述原始变量之间的相关关系,因此因子分析的出发点就是原始变量的相关系数矩阵 ,根据定义有
同时
上述两式称为正交因子模型的协方差结构,它将相关系数矩阵分解成X与F的协方差矩阵的乘积,受此启发,可以求出原始变量的相关系数矩阵 的谱分解式
为了使上式符合正交因子模型的假定,谱分解式中特征值 对应的特征向量
选为标准正交向量,同时
为对称矩阵,故当省略掉的最后 p-m 个特征值较小的时候,
可近似分解为
其中
上式给出的A和D就是因子模型的一个解. 因子载荷矩阵A中的第j列(即第j个公共因子 在X上的载荷)和X的第j个主成分的系数相差一个倍数
,故上式给出的解通常称为因子模型的主成分解.
因子个数m的确定原则,一般由实际情况或相关准则确定
或某下限值
2 因子分析模型与主成分分析模型的联系与区别
(今天来不及写了、很快补上
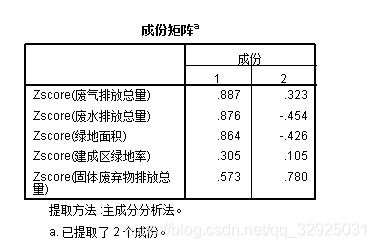
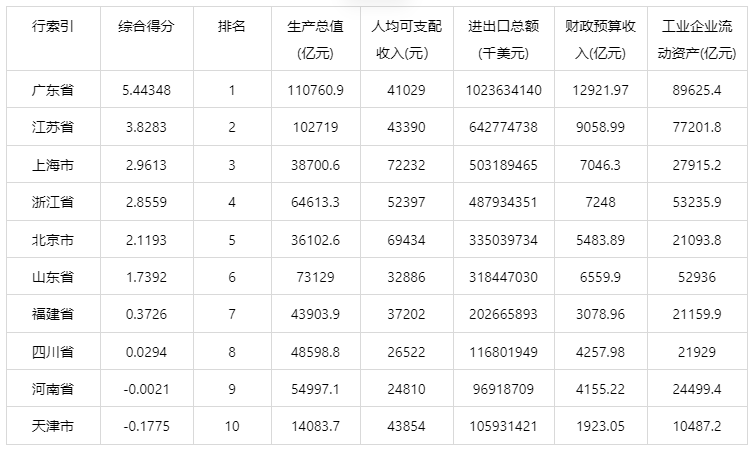
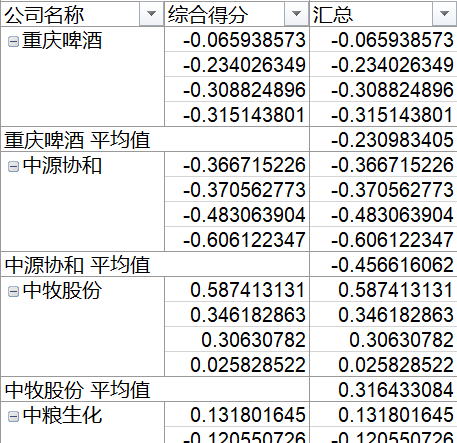
3 具体案例
(今天来不及写了、很快补上
* * * 分享 * 交流 :-) * * *