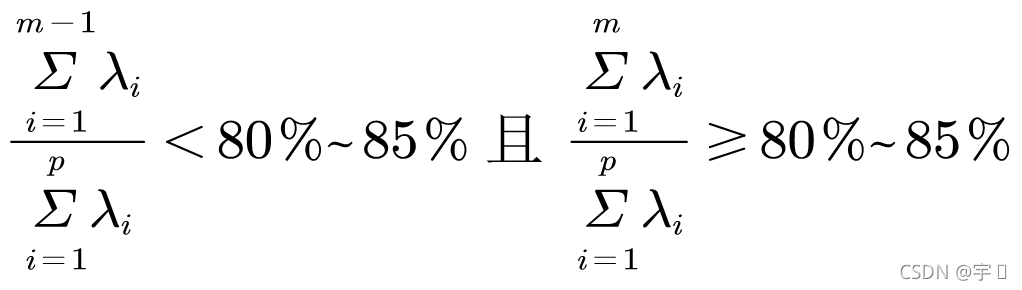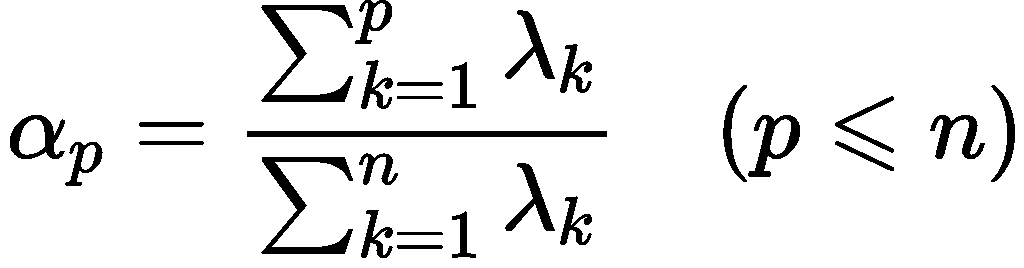主成分分析
本文将介绍主成分分析(PCA),主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。 一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
文章目录
- 主成分分析
- 一、主成分分析简介
- 二、主成分分析的思想
- 三、主成分分析的计算步骤
- 四、案例分析
- 五、模型扩展(★)
一、主成分分析简介
主成分分析可以用较少的新变量替换原来较多的新变量,而且是这些较少的新变量尽可能多地保留原来所反映的信息。
主成分分析是数据降维算法的一种,降维是将高维度的数据(指标太多)保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
二、主成分分析的思想
假设有 n n n 个样本, p p p 个指标,则可构成大小为 n × p n\times p n×p 的样本矩阵 x x x:
X = [ x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n p ] = ( x 1 , x 2 , ⋯ , x p ) X= \begin{bmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21}& x_{22} & \cdots &x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1}& x_{n2} & \cdots &x_{np} \end{bmatrix}=(x_1,x_2,\cdots,x_p) X=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1px2p⋮xnp⎦⎥⎥⎥⎤=(x1,x2,⋯,xp)
假设我们想找到新的一组变量 z 1 , z 2 , … , z m ( m ≤ p ) z_1,z_2,…,z_m( m ≤ p) z1,z2,…,zm(m≤p),且它们满足:
{ z 1 = l 11 x 1 + l 12 x 2 + ⋯ + l 1 p x p z 2 = l 21 x 1 + l 22 x 2 + ⋯ + l 2 p x p ⋯ z m = l m 1 x 1 + l m 2 x 2 + ⋯ + l m p x p \begin{cases} z_1=l_{11}x_1+l_{12}x_2+\cdots+l_{1p}x_p\\ z_2=l_{21}x_1+l_{22}x_2+\cdots+l_{2p}x_p\\ \cdots\\ z_m=l_{m1}x_1+l_{m2}x_2+\cdots+l_{mp}x_p \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧z1=l11x1+l12x2+⋯+l1pxpz2=l21x1+l22x2+⋯+l2pxp⋯zm=lm1x1+lm2x2+⋯+lmpxp
系数 l i j l_{ij} lij 的确定原则:
- z i z_i zi 与 z j z_j zj (i≠j; i,j=1,2,…,m) 相互无关;
- z 1 z_1 z1 是 x 1 , x 2 , . . . , x p x_1,x_2,...,x_p x1,x2,...,xp 的一切线性组合中方差最大者;
- z 2 z_2 z2 是与 z 1 z_1 z1 不相关的 x 1 , x 2 , . . . , x p x_1,x_2,...,x_p x1,x2,...,xp 的所有线性组合中方差最大者;
- 以此类推, z m z_m zm是与 z 1 , z 2 , … , z m − 1 z_1,z_2,…,z_{m-1} z1,z2,…,zm−1 不相关的 x 1 , x 2 , . . . , x p x_1,x_2,...,x_p x1,x2,...,xp 的所有线性组合中方差最大者;
- 新变量指标 z 1 , z 2 , … , z m z_1,z_2,…,z_m z1,z2,…,zm 分别称为原变量指标 x 1 , x 2 , . . . , x p x_1,x_2,...,x_p x1,x2,...,xp 的第一,第二,…,第 m m m 主成分。
三、主成分分析的计算步骤
假设有 n n n 个样本, p p p 个指标,则可构成大小为 n × p n×p n×p 的样本矩阵 x x x:
x = [ x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n p ] = ( x 1 , x 2 , ⋯ , x p ) x= \begin{bmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21}& x_{22} & \cdots &x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1}& x_{n2} & \cdots &x_{np} \end{bmatrix}=(x_1,x_2,\cdots,x_p) x=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1px2p⋮xnp⎦⎥⎥⎥⎤=(x1,x2,⋯,xp)
1. 首先对其进行标准化处理:
按 列 计 算 均 值 : x ˉ j = 1 n ∑ i = 1 n x i j , 标 准 差 : S j = ∑ i = 1 n ( x i j − x ˉ j ) 2 n − 1 , 标 准 化 数 据 : X i j = x i j − x ˉ j S j 原 始 样 本 矩 阵 经 过 标 准 化 变 化 : X = [ X 11 X 12 ⋯ X 1 p X 21 X 22 ⋯ X 2 p ⋮ ⋮ ⋱ ⋮ X n 1 X n 2 ⋯ X n p ] = ( X 1 , X 2 , ⋯ , X p ) 按列计算均值:\bar x_j=\frac{1}{n} \sum_{i=1}^{n}x_{ij},\quad 标准差:S_j=\sqrt{\frac{\displaystyle\sum_{i=1}^{n}(x_{ij}-\bar x_j)^2}{n-1}},\quad 标准化数据:X_{ij}=\frac{x_{ij}-\bar x_j}{S_j}\\ 原始样本矩阵经过标准化变化: X= \begin{bmatrix} X_{11} & X_{12} & \cdots &X_{1p} \\ X_{21}& X_{22} & \cdots &X_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ X_{n1}& X_{n2} & \cdots &X_{np} \end{bmatrix}=(X_1,X_2,\cdots,X_p) 按列计算均值:xˉj=n1i=1∑nxij,标准差:Sj=n−1i=1∑n(xij−xˉj)2,标准化数据:Xij=Sjxij−xˉj原始样本矩阵经过标准化变化:X=⎣⎢⎢⎢⎡X11X21⋮Xn1X12X22⋮Xn2⋯⋯⋱⋯X1pX2p⋮Xnp⎦⎥⎥⎥⎤=(X1,X2,⋯,Xp)
2. 计算标准化样本查的协方差矩阵:
R = [ r 11 r 12 ⋯ r 1 p r 21 r 22 ⋯ r 2 p ⋮ ⋮ ⋱ ⋮ r p 1 r p 2 ⋯ r p p ] R= \begin{bmatrix} r_{11} & r_{12} & \cdots &r_{1p} \\ r_{21}& r_{22} & \cdots &r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1}& r_{p2} & \cdots &r_{pp} \end{bmatrix} R=⎣⎢⎢⎢⎡r11r21⋮rp1r12r22⋮rp2⋯⋯⋱⋯r1pr2p⋮rpp⎦⎥⎥⎥⎤ r i j = 1 n − 1 ∑ k = 1 n ( X k i − X ‾ i ) ( X k i − X ‾ j ) = 1 n − 1 ∑ k = 1 n X k i X k j r_{ij}=\frac{1}{n-1}\sum_{k=1}^{n}{(X_{ki}-\overline X_i)(X_{ki}-\overline X_j)}=\frac{1}{n-1}\sum_{k=1}^{n}{X_{ki}X_{kj}} rij=n−11k=1∑n(Xki−Xi)(Xki−Xj)=n−11k=1∑nXkiXkj
1、2步骤可以合成一步:
R = ∑ k = 1 n ( x k i − x ‾ i ) ( x k i − x ‾ j ) ∑ k = 1 n ( x k i − x ‾ i ) 2 ∑ k = 1 n ( x k j − x ‾ j ) 2 R=\frac{\displaystyle\sum_{k=1}^{n}{(x_{ki}-\overline x_i)(x_{ki}-\overline x_j)}}{\sqrt{\displaystyle\sum_{k=1}^{n}{(x_{ki}-\overline x_i)^2}\sum_{k=1}^{n}{(x_{kj}-\overline x_j)^2}}} R=k=1∑n(xki−xi)2k=1∑n(xkj−xj)2k=1∑n(xki−xi)(xki−xj)
3. 计算 R 的特征值和特征值向量:
特 征 值 λ 1 ≥ λ 2 ≥ ⋯ ≥ λ p ≥ 0 , ( R 是 半 正 定 矩 阵 , 且 t r ( R ) = ∑ k = 1 p λ k = p ) 特 征 向 量 : a 1 = [ a 11 a 21 ⋮ a p 1 ] , a 2 = [ a 12 a 22 ⋮ a p 2 ] , ⋯ , a p = [ a 1 p a 2 p ⋮ a p p ] 特征值 \lambda_1≥\lambda_2≥\cdots≥\lambda_p≥0,\quad(R是半正定矩阵,且tr(R)=\sum_{k=1}^{p}\lambda_k=p)\\ 特征向量:a_1=\left[ \begin{array}{c} a_{11}\\a_{21}\\ \vdots\\a_{p1} \end{array} \right],a_2=\left[ \begin{array}{c} a_{12}\\a_{22}\\ \vdots\\a_{p2} \end{array} \right],\cdots,a_p=\left[ \begin{array}{c} a_{1p}\\a_{2p}\\ \vdots\\a_{pp} \end{array} \right] 特征值λ1≥λ2≥⋯≥λp≥0,(R是半正定矩阵,且tr(R)=k=1∑pλk=p)特征向量:a1=⎣⎢⎢⎢⎡a11a21⋮ap1⎦⎥⎥⎥⎤,a2=⎣⎢⎢⎢⎡a12a22⋮ap2⎦⎥⎥⎥⎤,⋯,ap=⎣⎢⎢⎢⎡a1pa2p⋮app⎦⎥⎥⎥⎤
4. 计算主成分共享率以及累计贡献率:
贡 献 率 = λ i ∑ k = 1 p λ k , 累 加 贡 献 率 = ∑ k = 1 i λ k ∑ k = 1 p λ k , ( i = 1 , 2 , ⋯ , p ) 贡献率=\frac{\lambda_i}{\displaystyle\sum_{k=1}^{p}{\lambda_k}},\quad累加贡献率=\frac{\displaystyle\sum_{k=1}^{i}{\lambda_k}}{\displaystyle\sum_{k=1}^{p}{\lambda_k}},\quad(i=1,2,\cdots,p) 贡献率=k=1∑pλkλi,累加贡献率=k=1∑pλkk=1∑iλk,(i=1,2,⋯,p)
5. 写出主成分:
一般取累计贡献率超过 80% 的特征值所对应的第一、第二、…、第 m m m( m ≤ p m≤p m≤p)个主成分。
第 i 个 主 成 分 : F i = a 1 i X 1 + a 2 i X 2 + ⋯ + a p i X p 第i个主成分:F_i = a_{1i}X_1+a_{2i}X_2+\cdots+a_{pi}X_p 第i个主成分:Fi=a1iX1+a2iX2+⋯+apiXp
6. 根据系数分析主成分代表的意义:
对于某个主成分而言,指标前面的系数越大,代表该指标对于该主成分的影响越大。
四、案例分析
题目来源于:《应用多元统计分析》王学民
在制定服装标准的过程中,对128名成年男子的身材进行了测量,每人测得的指标中含有这样六项:身高( x 1 x_1 x1)、坐高( x 2 x_2 x2) 、胸围( x 3 x_3 x3) 、手臂长( x 4 x_4 x4) 、肋围( x 5 x_5 x5)和腰围( x 6 x_6 x6) 。所得样本相关系数矩阵(对称矩阵哦)列于下表。

注意:本题相当于直接把 第一二步骤计算好,但是我们在建模的时候得到的是最原始的数据(每一列是指标,每一行是样本)。
经过计算,相关系数矩阵的特征值、相应的特征向量以及贡献率列于下表:

注意:matlab 求得的特征值向量,默认进行了归一化,验证方法:每一列平方和之后开根号。
从表中可以看到前三个主成分的累计贡献率达85.9%,因此可以考虑只取前面三个主成分,它们能够很好地概括原始变量。

X i X_i Xi 均是标准化后的指标, x i x_i xi:身高、坐高、胸围、手臂长、肋围和腰围
- 第一主成分 F 1 F_1 F1 对所有(标准化)原始变量都有近似相等的正载荷,故称第一主成分为(身材)大小成分。
- 第二主成分 F 2 F_2 F2 在 X 3 X_3 X3、 X 5 X_5 X5、 X 6 X_6 X6。上有中等程度的正载荷,而在 X 1 X_1 X1、 X 2 X_2 X2、 X 4 X_4 X4 上有中等程度的负载荷,称第二主成分为形状成分(或胖瘦成分)。
- 第三主成分 F 3 F_3 F3 在 X 2 X_2 X2 上有大的正载荷,在 X 4 X_4 X4 上有大的负载荷,而在其余变量上的载荷都较小,可称第三主成分为臂长成分。
注:由于第三主成分的贡献率不高( 7.65%)且实际意义也不太重要,因此我们也可以考虑只取前两个主成分进行分析。
五、模型扩展(★)
- 主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。
- 主成分分析的困难之处主要在于要 能够给出主成分的较好解释,所提取的主成分中如有一个主成分解释不了,整个主成分分析也就失败了。
- 主成分分析不可用于评价类模型。
- 主成分分析可用于聚类分析,将自变量进行降维方便画图。
- 主成分分析也可用于回归分析解决多重共线性的问题。
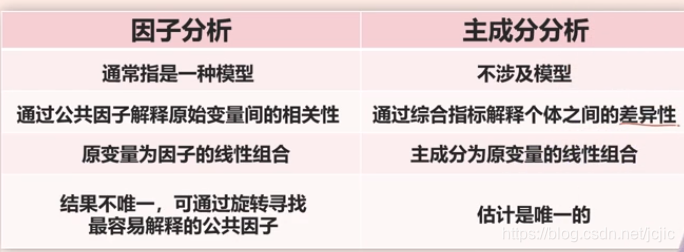
- 主成分分析实际上是因子分析的特例,但是由于因子分析便于解释,所以建议大家多用因子分析。
本文借鉴了数学建模清风老师的课件与思路,如果大家发现文章中有不正确的地方,欢迎大家在评论区留言,也可以点击查看下方链接查看清风老师的视频讲解~
原文链接:https://www.bilibili.com/video/BV1DW411s7wi