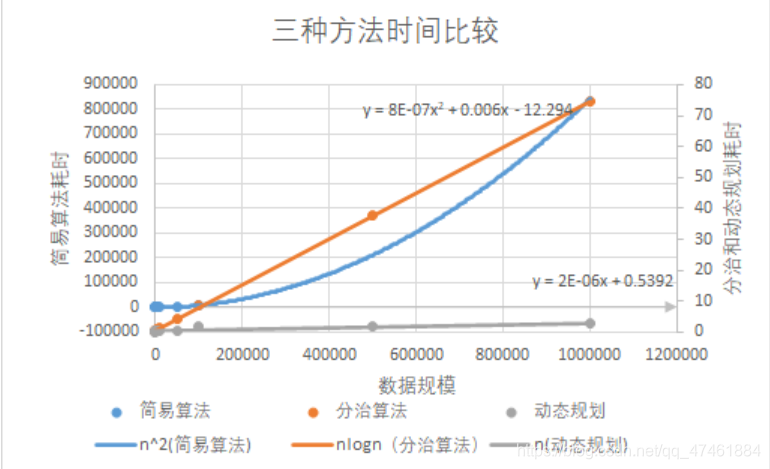
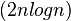什么是最大子段和，通俗点讲：
最大子段和就是给了一些数，然后你从中找了几个连续的数，这组连续的数的和比任意一组连续的数的和都大，那么你找的这几个连续的数的和就是这些数的最大子段和。
通俗的听不懂你就看这里：
给定由n个整数（可能为负整数）组成的序列,
...
,求该序列形如
的子段和的最大值。当所有整数均为负整数时定义其最大子段和0。依此定义，所求的最优值为：
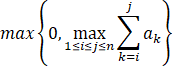。例如，当(a1,a2,a3,a4,a5,a6)=(-2,11,-4,13,-5,-2)时，最大子段和为
= 20。
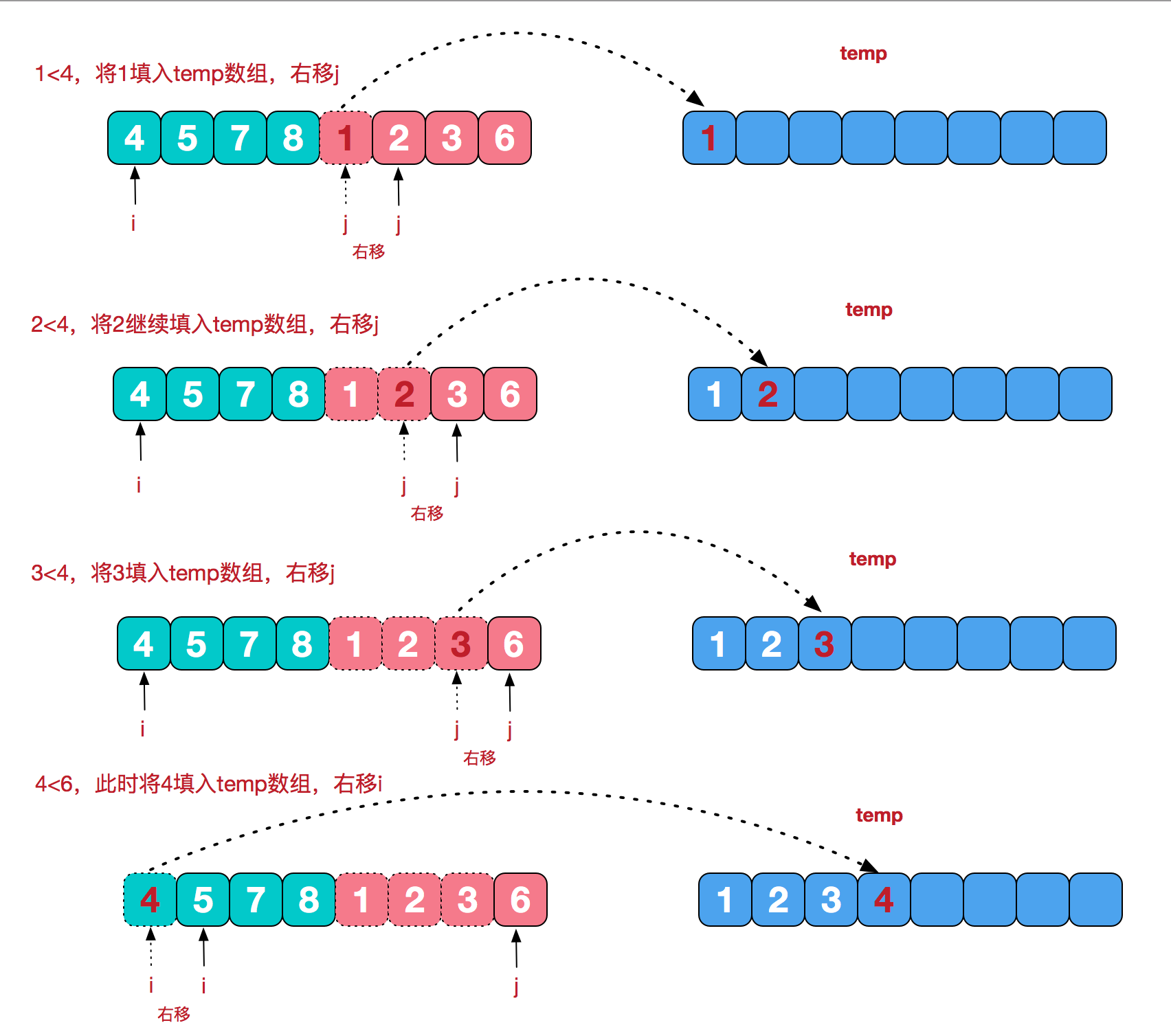
一、分治法
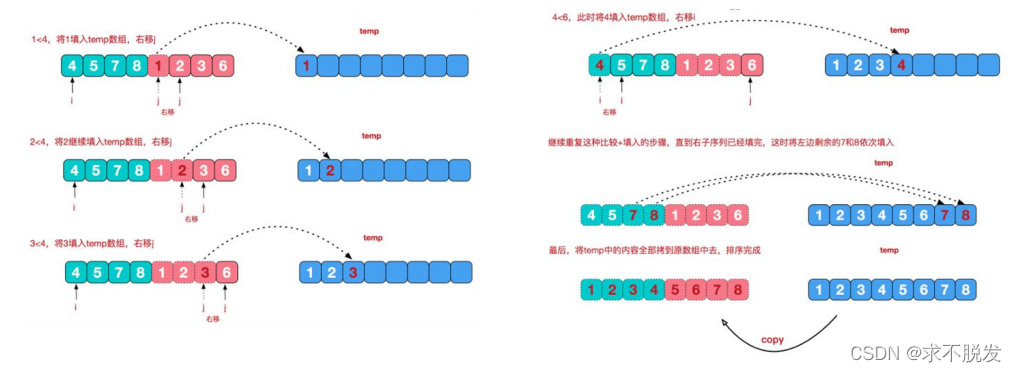
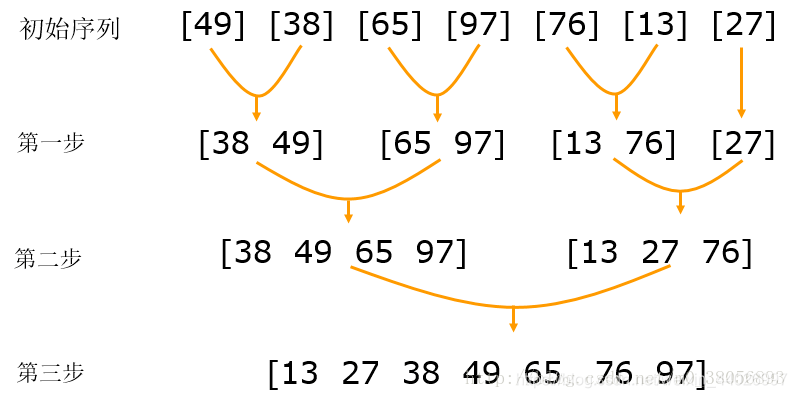
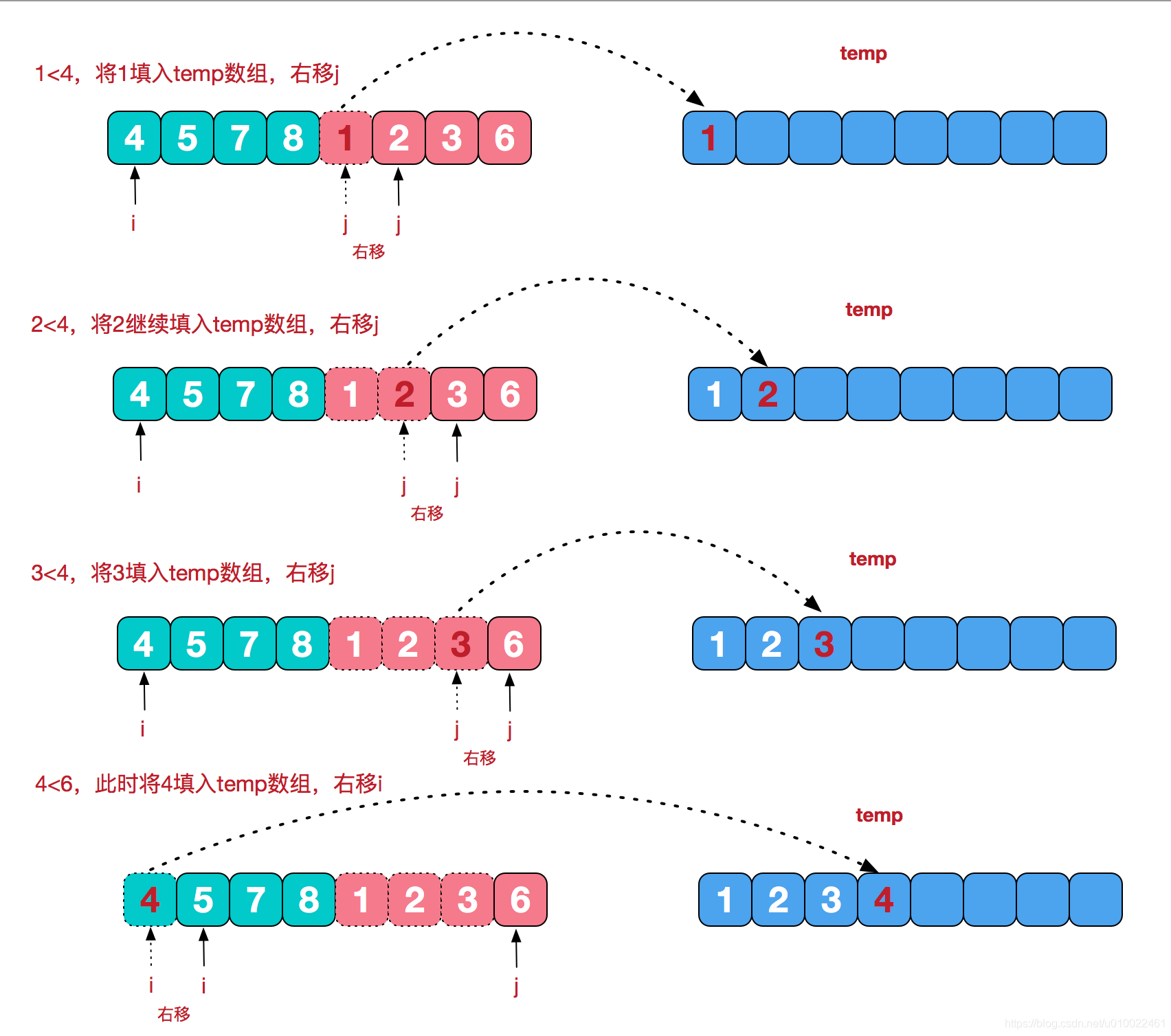
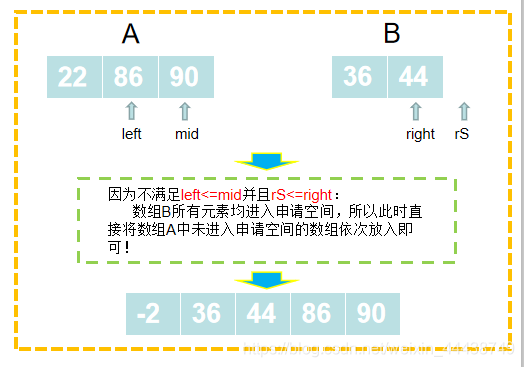
分治法思想：如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n]，分别求出这两段的最大子段和，则a[1:n]的最大子段和有三种情形：（不敲了。。。直接看图）
#include<iostream>
using namespace std;
int MaxSubSum(int *a,int left,int right){int sum = 0;if(left == right)sum = a[left] > 0 ? a[left] : 0;else{int center = (left + right)/2;int leftsum = MaxSubSum(a, left, center);int rightsum = MaxSubSum(a,center+1,right);int s1 = 0;int lefts = 0;for(int i =center;i>=left;i--){lefts +=a[i];if(lefts > s1)s1 = lefts;} int s2 = 0;int rights = 0;for(int j = center +1;j<=right;j++){rights += a[j];if(rights> s2)s2 = rights;}sum = s1+s2;if(sum<leftsum)sum = leftsum;if(sum<rightsum)sum = rightsum;}return sum;
}int MaxSum(int n,int *a){return MaxSubSum(a,0,n);
}int main(){int a[] ={-2,11,-4,13,-5,-2};cout<<"最大子段和是:"<<MaxSum(5,a)<<endl;return 0;
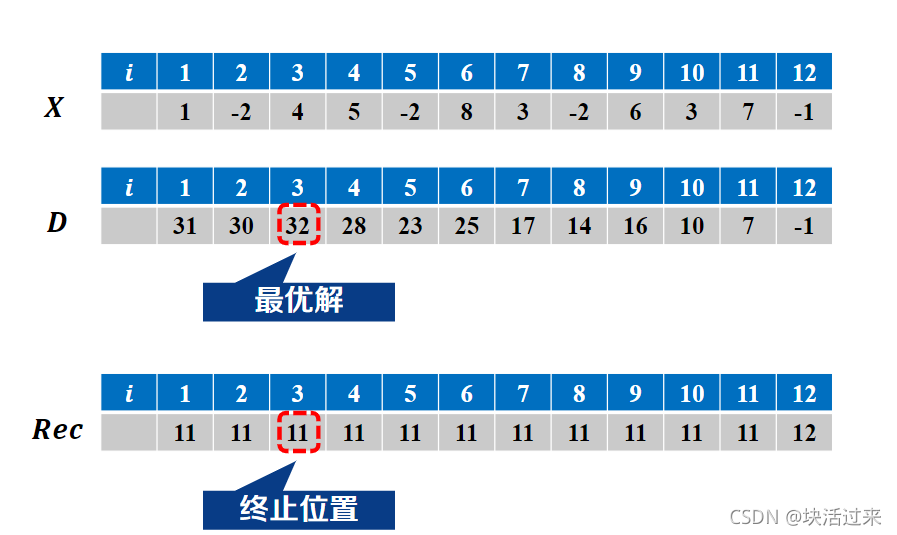
}二、动态规划
动态规划思想：设b[i]是以第i个数结尾的最大子段和，那么从a[i]的角度来看，b[i]的值只有两种情况，如果 b[i-1]>0,那么b[i]=b[i-1]+a[i]，否则b[i]=a[i]。（我觉得这个说法比书上的好理解）。
#include<iostream>
using namespace std;
int MaxSum(int n,int *a){int sum = 0, b = 0;for(int i =0;i<n;i++){if(b>0)b+=a[i];elseb = a[i];if(b>sum)sum = b;}return sum;
}
int main(){int a[] = {-2,11,-4,13,-5,-2};cout<<"最大子段和:"<<MaxSum(5,a)<<endl;return 0;
}
