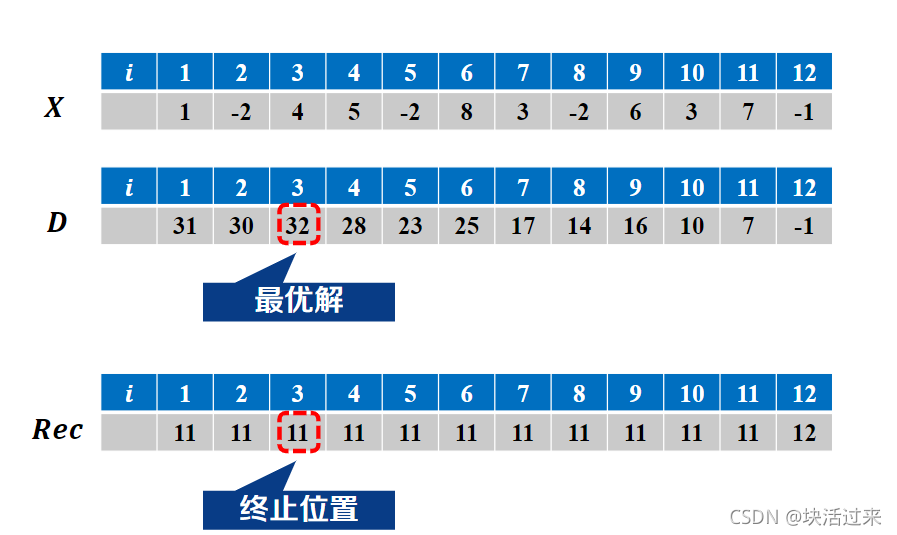
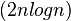给定由n个整数(可能为负整数)组成的序列a1,a2, a3… , an, 寻找它的某个连续子段,使得其和最大。例如( -2,11,-4,13,-5,-2 )最大子段是{ 11,-4,13 }其和为20。
1、最大字段和问题的简单算法
(1)枚举法求解:
以a[0]开始: {a[0]}, {a[0],a[1]},{a[0],a[1],a[2]}……{a[0],a[1],……a[n]}共n个
以a[1]开始: {a[1]}, {a[1],a[2]},{a[1],a[2],a[3]}……{a[1],a[2],……a[n]}共n-1个
……
以a[n]开始:{a[n]}共1个
#include<iostream>
using namespace std;int maxSum(int n, int a[], int &besti, int &bestj){int sum = 0;for(int i= 0; i < n; i++) {int thisSum = 0;for(int j = i; j < n; j++){thisSum += a[j];if(thisSum > sum){sum = thisSum;besti = i;bestj = j;}}}return sum;
}int main(){int a[] = {-2,11,-4,13,-5,-2,};for(int i=0; i<6; i++){cout<<a[i]<<" ";}int besti,bestj;cout<<endl;cout<<"数组a的最大连续子段和为:a["<<besti<<":"<<bestj<<"]:"<<maxSum(6,a,besti,bestj)<<endl;return 0;
}

2、最大字段和问题分治算法:
将序列a[1:n]分成长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大字段和,则a[1:n]的最大子段和有三中情形:
-
a[1:n]的最大子段和与a[1:n/2]的最大子段和相同;
-
a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同;
-
a[1:n]的最大字段和为

,且1<=i<=n/2,n/2+1<=j<=n。
可用递归方法求得情形1、2。对于情形3,可以看出a[n/2]与a[n/2+1]在最优子序列中。因此可以在a[1:n/2]中计算出
,并在a[n/2+1:n]中计算出 。则s1+s2即为出现情形3时的最优值。
。则s1+s2即为出现情形3时的最优值。
#include<iostream>
using namespace std;int maxSubSum(int a[], int left, int right){int sum = 0;if(left == right){sum = a[left]>0 ? a[left] : 0;}else{int center = (left + right) / 2;int leftSum = maxSubSum(a, left, center);int rightSum = maxSubSum(a, center + 1, right);int s1 = 0;int lefts = 0;for(int i = center; i >= left; i--){lefts += a[i];if(lefts > s1) s1 = lefts;}int s2 = 0;int rights = 0;for(int i = center + 1; i < right; i++){rights += a[i];if(rights > s2) s2 = rights;}sum = s1 + s2;if(sum < leftSum) sum = leftSum; if(sum < rightSum) sum = rightSum;}return sum;
}int maxSum(int a[], int n){return maxSubSum(a, 0, n - 1);
}int main(){int a[] = {-2,11,-4,13,-5,-2,};// left rightfor(int i= 0; i < 6; i++){cout<<a[i]<<" ";} cout<<endl;cout<<"数组a的最大连续子段和为:" << maxSum(a, 6)<<endl;return 0;
}

O(nlogn)
3、动态规划算法:
#include<iostream>
using namespace std;int maxSum(int a[], int n){int sum = 0;int b = 0;for(int i = 0; i < n; i++){if(b > 0)b += a[i]; elseb = a[i];if(b > sum)sum = b;}return sum;
}int main(){int a[] = {-2,11,-4,13,-5,-2,6};for(int i= 0; i < 7; i++){cout<<a[i]<<" ";} cout<<endl;cout<<"数组a的最大连续子段和为:" << maxSum(a, 7)<<endl;return 0;
}

4、最大子段和问题动态规划算法推广:
一、最大子矩阵和:
二、最大m子段和问题: