归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

1.算法思想

第一步：将待排序列不断二分，直到分成每个元素单独为一个子序列时停止，此时所有子序列均为有序（因为只有一个元素）；
第二步：申请一个空间大小为两个待合并子序列空间之和，用来存放两个子序列归并后的序列；
第三步：设置两个指针，初始时分别指向两个待合并子序列的起始元素处；
第四步：比较两个指针所指向的元素大小，选择两者中较小的元素，放入到步骤二申请的空间中，并移动刚刚较小元素的指针到子序列的下一位置；
第五步：不断重复第四步，直到某一指针移出子序列的结尾，此时，将另一子序列中剩余未添加到申请空间的元素添加进申请空间中；

2.图解

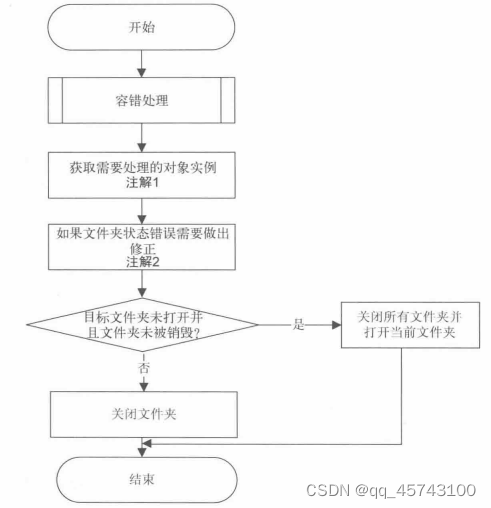
2.1算法流程：

在这里插入图片描述

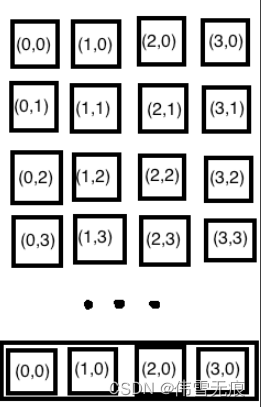
2.2接下来对上图中合的过程进行详细图解说明，以橙色虚线框中为例：

第一步：
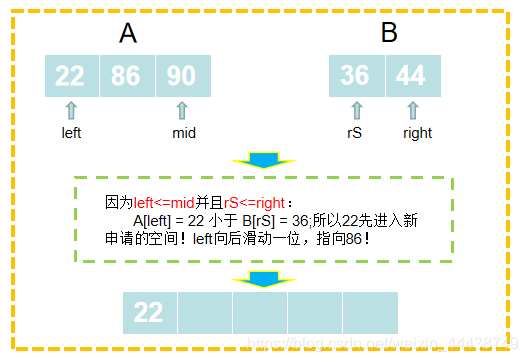
在这里插入图片描述
第二步：

第三步：

第四步：

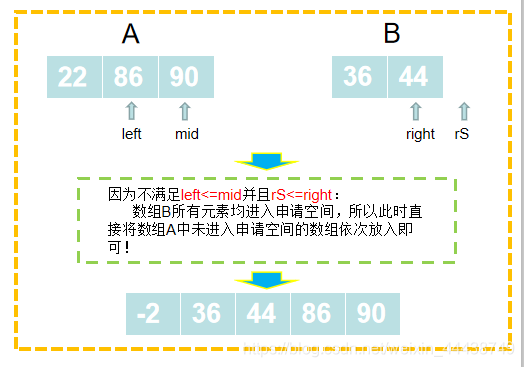
3.算法分析

归并排序是稳定的排序，即相等的元素的顺序不会改变。速度仅次于快速排序，一般用于对总体无序，但是各子项相对有序的数列，归并排序的比较次数小于快速排序的比较次数，移动次数一般多于快速排序的移动次数。
时间复杂度 O(nlogn)
空间复杂度 T（n)

4.代码实现

public class MergrSort {//归并排序-------------------------------------------------------------public void mergeSort(int[] a,int left,int right){if(left<right){int middle = (left + right)/2;mergeSort(a,left,middle);mergeSort(a,middle+1,right);merge(a,left,middle,right);}else if(left == right)return;}private void merge(int[] a, int left, int middle, int right) {int[] tempArray = new int[a.length];int rS = middle + 1;int temp = left;int third = left;//比较两个小数组相应下标位置的数组大小，小的先放进新申请的空间数组while(left<=middle&&rS<=right){if(a[left]<=a[rS]){tempArray[third++] = a[left++];}else {tempArray[third++] = a[rS++];}}//如果左边还有数据需要拷贝，把左边数组剩下的拷贝到新申请的空间数组while (left<= middle){tempArray[third++] = a[left++];}//如果右边还有数据需要拷贝，把右边数组剩下的拷贝到新申请的空间数组while (rS<= right){tempArray[third++] = a[rS++];}while (temp<=right){a[temp] = tempArray[temp++];}}//----------------------------------------------------------------------//测试代码public static void main(String[] args) {MergrSort mergrSort = new MergrSort();int[] a={25,33,-2,55,43,90,86,22,44,36};System.out.println("排序之前：");for(int i=0;i<a.length;i++){System.out.print(a[i]+"  ");}mergrSort.mergeSort(a,0,a.length-1);System.out.println();System.out.println("排序之后：");for(int i=0;i<a.length;i++){System.out.print(a[i]+"  ");}}
}