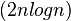3种算法：最大子段求和

一、问题分析

问题：给定有n个整数(可能为负整数)组成的序列$a_1,a_2,...,a_n,$求该序列连续的子段和的最大值。 如果该子段的所有元素和是负整数时定义其最大子段和为0。

简易算法： 两层循环遍历全部可能值，找出最大的记录下来。先从 $i$ 加到 $j$ 如果出现负数，同时记录当前循环的最大值，并且 $j++$；然后再 $i++$ 进行下一趟遍历，找可能的最大值。

分治算法： 在序列中间对问题进行划分，划分得到两段序列；其最大子段和可能出现在三个位置以及求解方法：

1. 出现在左边$(left)$子段 ——计算 $left$ 到 $center$ 的最大和，记作 $leftSum$。
2. 出现在右边$(right)$子段 ——计算从 $center+1$ 到 $right$ 的最大和，记作 $rightSum$ 。
3. 出现在跨中间 ($center$)子段 —— 从 $center$ 出发分别向左右扩展，同时记录分别的 $s_1$ 和 $s_2$ 扩张到值不再增大；这种情况下的值为 $centerSum=s_1+s_2$ 。

此时最大子段和$sum=max(leftSum,rightSum,centerSum)$ 。

动态规划算法： 该问题可分为两个阶段：①累加和为负不进行最大和计算，同时将sum值置为0 ②累加和为正时，开始累加。

二、复杂度分析

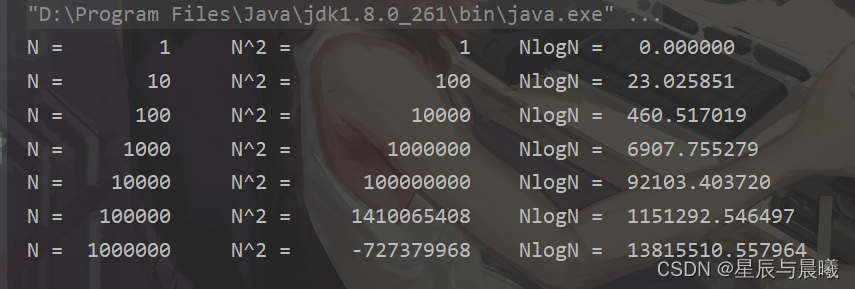
简易算法： 两层 $for$ 循环需要 $O(n^2)$ 的计算时间。

分治算法： 递归式
$$T(n)=\{\begin{array}{ll}O(1),& n\le c\\ 2T(n/2)+O(n),& n>c\end{array}$$
由主函数计算方法可以得到 $T(n)=O(n\log (n))$ 。

动态规划算法: 明显只有一层循环，只有 $O(n)$ 的计算时间和空间。

三、程序实现和测试过程和结果

简易算法：

int sum =0;int besti=0;int bestj=0;for(int i =0;i<n;i++){int thissum =0;for(int j=i;j <n;j++){thissum += a[j];if(thissum > sum){sum = thissum;besti = i;bestj = j;}}}

分治算法：

int maxSubSum(int left, int right)
{int sum =0;if(left == right)sum = a[left] >0? a[left]:0;  // 问号冒号表达式else{int center = (left+right)/2;int leftsum = maxSubSum(left,center);  // 递归求解int rightsum = maxSubSum(center+1,right);  // 递归求解// 向左扩张int s1=0;int lefts=0;for(int i = center;i>=left;i--){lefts += a[i];if(lefts>s1) s1= lefts;}// 向右扩张int s2 = 0;int rights = 0;for(int i = center+1;i<=right;i++){rights += a[i];if(rights>s2) s2= rights;}sum = s1+s2;// 取三种情况的最大值if(sum <leftsum) sum = leftsum;if(sum <rightsum) sum = rightsum;}return sum;}

动态规划算法:

int maxSum()
{int sum =0;int b=0;for(int i=0;i<n;i++){if(b>0) b+=a[i];  // 正数则继续else b= a[i];  // 否则直接从下一位开始计算if(b>sum) sum=b;}return sum;
}

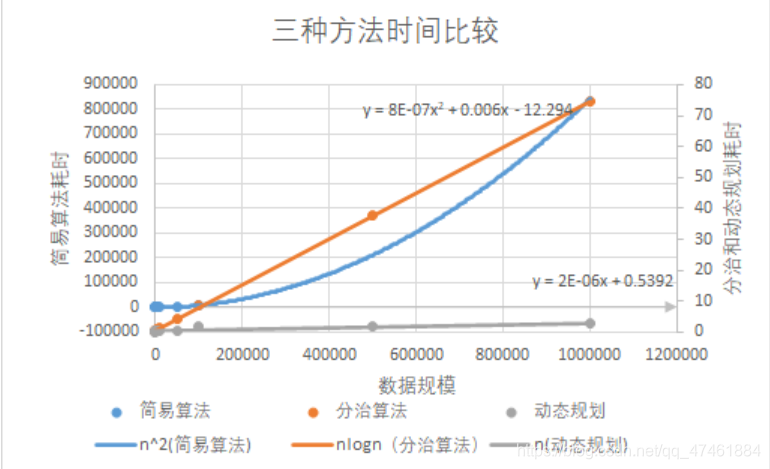
对文件数据读取处理的时间进行统计拟合，发现耗时和预期基本一致。

四、总结问题

在上图中虽然不太明显，但是在动态规划算法中5000规模的数据那一栏，耗时反而增加，经过多次重复计算，多次采取其他计算方法，仍然出现耗时增加，暂未分析出原因。
另外这个画图好麻烦，感觉不会调坐标轴。