最大子段和（动态规划算法）

一、思路

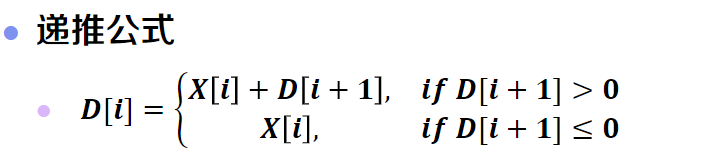
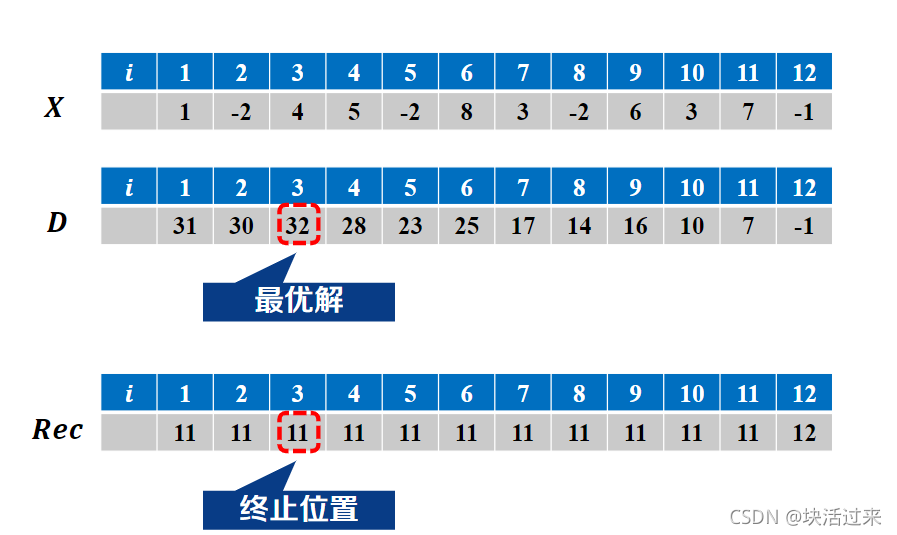
D[i]表示从i开始的最大字段和。（但我们不是从前往后找字段结束位置）
根据递推公式，我们可知要想求得D[i],就必须知道D[i+1],所以我们从前往后计算。
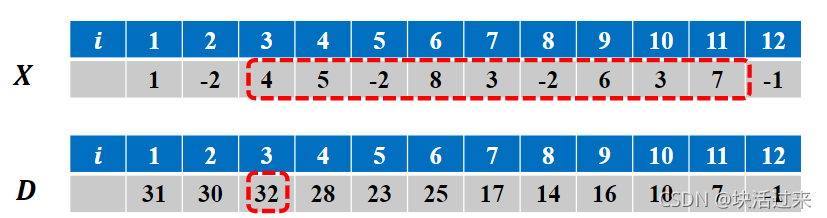
如下图：以i=12开始的子段和D[12]=X[12]=-1，该子段结束位置Rec[12]=i=12；
当i=11时，D[11+1]<0,所以D[11]=X[11]=7,Rec[i]=i=11;
当i=10时，D[10+1]>0,所以D[10]=X[10]+D[11]=3+7,Rec=i+1=11;
…
一直到i，我们就找完了所有子段和，接着在子段和中找最大的。

二、伪代码

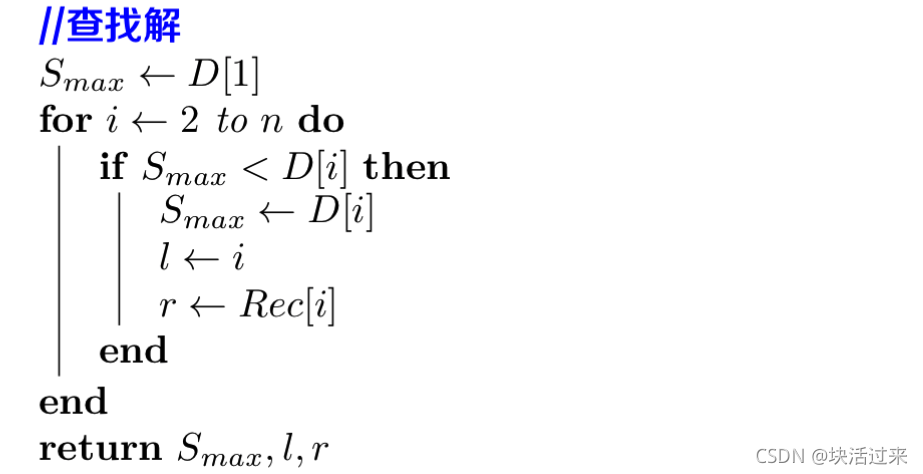
三、C++代码

#include <iostream>using namespace std;void Dsum(int n,int X[],int D[],int Rec[])
{int sum=D[1],l,r;for(int i=2;i<=n;i++){if(sum<D[i]){sum=D[i];l=i;r=Rec[i];}}cout<<"最长字段和为："<<sum<<endl;cout<<"最长字段为：";for(int i=l;i<=r;i++)cout<<X[i]<<' ';cout<<endl;
}
void find(int n,int X[])
{//X[]中为数组的值int D[n+1],Rec[n+1];//D[]中为以i为首的最大子段//Rec[]中记录了每个字段的尾数字的位置D[n]=X[n];//Rec[n]=n;for(int i=n-1;i>0;i--){//采用从后往前的计算if(D[i+1]>0){D[i]=X[i]+D[i+1];Rec[i]=Rec[i+1];}else{D[i]=X[i];Rec[i]=i;}}Dsum(n,X,D,Rec);//该函数用来寻找最大子段和，以及该子段的开始和结束位置
}
int main()
{int n;cout<<"请输入数组长度n:\n";cin>>n;int X[n+1];//为了方便，每个数组都是1~n（而不是0~n-1）cout<<"请输入数组:\n";for(int i=1;i<=n;i++)cin>>X[i];find(n,X);//该函数用来生成子段和return 0;
}
/*
12
1 -2 4 5 -2 8 3 -2 6 3 7 -1
*/

四、输入实例