一、题目

二、算法求解

1、蛮力算法

伪代码

算法分析

程序

2、分治策略

伪代码

算法分析

程序

3、动态规划算法

伪代码

算法分析

程序

一、题目

设A=<a1,a2,...,an>是n个整数的序列，称<ai,....,aj>为该序列的连续子序列，其中1<=i<=j<=n，子序列的元素之和 $\sum_{k=i}^{j} a_{k}$ 称为A的子段和：

例如，A=<-2,11,-4,13,-5,-2>，那么它的子段和如下：

长度为1的子段和有：-2,11,-4,13,-5,-2

长度为2的子段和有：9,7,9,8,-7

长度为3的子段和有：5,20,4,6

长度为4的子段和有：18,15,2

长度为5的子段和有：13,13

长度为6的子段和有：11

其中的最大子段和为：11-4+13=20

则最大子段和问题为：

给定n个整数的序列A=<a1,a2,...,an>，求

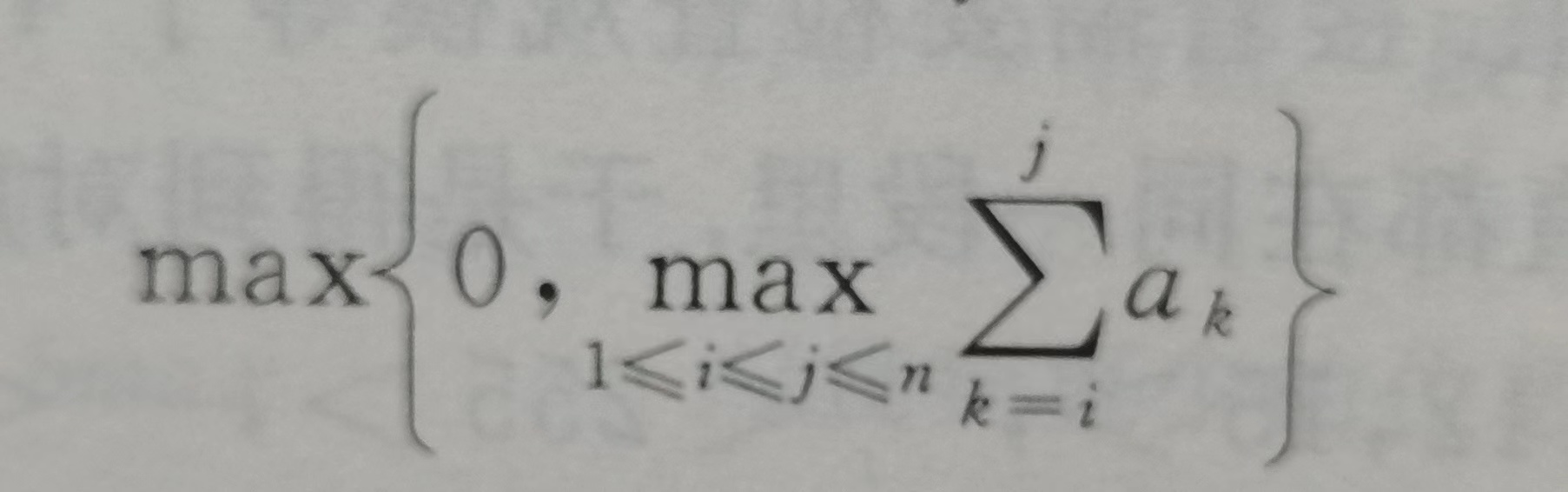
二、算法求解

1、蛮力算法

通过枚举A的所有连续子序列并且求和，通过比较找出具有最大和的子序列。

伪代码

//算法 Enumerate
//输入：数组A[1..n]
//输出：sum,first,last   //sum为最大子段和，first与last分别是和的首末位置

$sum\leftarrow 0$
$for \quad i\leftarrow 1 \quad to \quad n \quad do$
      $for \quad j\leftarrow 1\quad to \quad n \quad do$
                $thissum\leftarrow 0$
               $for \quad k\leftarrow i \quad to \quad j \quad do$
      $if \quad thissum>sum$
      $then \quad sum\leftarrow thissum$
                $first\leftarrow i$
                $last\leftarrow j$

算法分析

3个for循环，每次执行O(n)次，循环内部是常数操作，所以该算法的时间复杂度为 $O(n^{3})$

程序

//算法3.8 Enumerate
//输入：数组A[1..n]
//输出：sum,first,last#include<stdio.h>
#include<stdlib.h>
void Enumerate (int a[],int n)
{int sum = 0;int i,j,k;int first,last;for(i = 0;i < n; i++){for(j = i;j < n;j++){int thissum = 0;for(k = i;k <= j; k++){thissum = thissum + a[k];}if(thissum > sum){sum = thissum;first = i;last = j;}}}printf("数组A的最大连续子段和为A[%d..%d]=%d",first+1,last+1,sum);
}int main()
{int A[6]={-2,11,-4,13,-5,-2};int i;for(i = 0;i < 6;i++){printf("%d ",A[i]);}printf("\n");Enumerate(A,6); return 0;
}

2、分治策略

与最邻近点对的算法（参考之前的文章）类似，我们可以在 n/2的位置将 A 划分成A1和 A2前后两半，于是 A 的最大子段和可能是三种情况：

出现在 A1部分
出现在 A 部分，
出现在横跨两边的中间部分

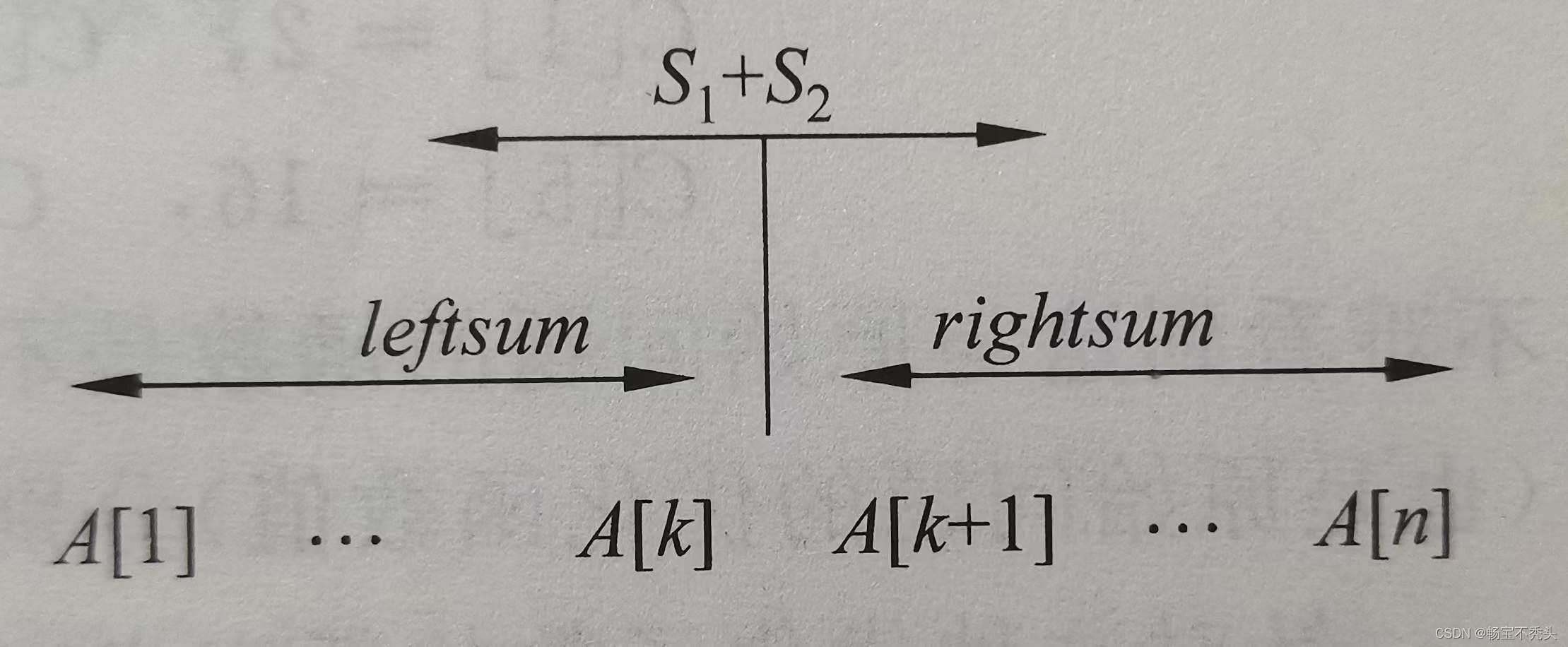
前两种情况恰好对应于两个规模减半的子问题，第三种情况需要特殊处理一下，设原问题的输人是 A [1...n]，中间分点 k = n /2，那么前半部分子问题的输人是 A [1...k]，后半部分子问题的输人是 A [ k +1，n]。在第三种情况下，设这个最大和是 A [ p .. q ]，那么 $p\leq k$ , $q\geq k+1$ ，从 A [ p ］到 A [ k ］的元素都在 A1 中，从 A [ k 十1］到 A [ q ］的元素都在 A2 中，我们只需要从 A [ k ］和 A [ k +1］分别向前和向后求和即可，比如以 A [ p ...k ］的计算为例，依次计算 A [ k .. k ], A [ k-1, k ],.., A [1...k]，记下其中最大的和 S1 ，即 A [ p ... k ]，对右半部可以同样处理，只不过扫描方向相反，得到的 S2 就是 A [ k+1... q ］的元素之和，当两个方向的扫描都完成之后,S1+S2 就是横跨中心的最大和，其边界从p到q。这三种情况都计算完成以后，通过比较就可以确定 A 的最大子段和

伪代码

//MaxSubSum(A,left,right) 【分治算法】
//输入：数组A,left,right分别是A的左右边界，1<=left<=right
//输出：A的最大子段和sum及其子段的前后边界

$if \quad left=right \quad then \quad return \quad max\left \{ A[left],0 \right \}$
$center\leftarrow (left+right)/2$
$leftsum\leftarrow MaxSubSum(A,left,center)$
$rightsum\leftarrow MaxSubSum(A,center+1,right)$
$S_{1}\leftarrow A_{1}[center]$
$S_{2}\leftarrow A_{2}[center+1]$
$sum\leftarrow S_{1}+S_{2}$
$if\quad leftsum>sum \quad then \quad sum\leftarrow leftsum$
$if \quad rightsum>sum \quad then \quad sum\leftarrow rightsum$

算法分析

设算法对规模为的输人运行时间是 T ( n )，行3和行4是递归调用，每个子问题是原来问题规模的一半，因此需要2T( n /2）时间，行5和行6的处理需要扫描A的每个元素，总计需要O(n)时间，于是递归方程为：

$T(n)=2T(n/2)+O(n), \quad\quad T(1)=0$

该方程的解为： $T(n)=O(n\log n)$

程序

//算法3.9 MaxSubSum(A,left,right) 【分治算法】 
//输入：数组A,left,right分别是A的左右边界，1<=left<=right
//输出：A的最大子段和sum及其子段的前后边界#include<stdio.h>
#include<stdlib.h>typedef struct max_info{int low;int high;int sum;
};struct max_info MaxSubSum(int a[],int left,int right)
{struct max_info maxinfo;maxinfo.sum = 0;int i;if(left == right){maxinfo.sum = a[left]>0 ? a[left] : 0;maxinfo.high = right;maxinfo.low = right;return maxinfo;}else{struct max_info leftinfo;//左侧 struct max_info rightinfo;//右侧 struct max_info croseinfo;//跨越 int center = (left + right) / 2;leftinfo = MaxSubSum(a, left, center);rightinfo = MaxSubSum(a, center + 1, right);int s1 = 0;int suml = 0;for(i = center; i >= left; i--){			suml += a[i];if(suml > s1) {s1 = suml;croseinfo.low = i;}	}int s2 = 0;int sumr = 0;for(i = center + 1; i < right; i++){			sumr += a[i];if(sumr > s2){s2 = sumr;croseinfo.high = i;	}	}croseinfo.sum = s1 + s2;if(croseinfo.sum < leftinfo.sum){maxinfo.sum = leftinfo.sum;	maxinfo.high = leftinfo.high;maxinfo.low = leftinfo.low;} 			if(croseinfo.sum < rightinfo.sum){maxinfo.sum = rightinfo.sum;maxinfo.high = rightinfo.high;maxinfo.low = rightinfo.low;} else{maxinfo.sum = croseinfo.sum;maxinfo.high = croseinfo.high;maxinfo.low = croseinfo.low;}}return maxinfo;
}int main()
{struct max_info maxinfo;int A[6]={-2,11,-4,13,-5,-2};int i;for(i = 0;i < 6;i++){printf("%d ",A[i]);}printf("\n");maxinfo = MaxSubSum(A,0,5); printf("数组A的最大连续子段和为：A[%d..%d]=%d\n",maxinfo.low+1,maxinfo.high+1,maxinfo.sum);return 0;
}

3、动态规划算法

为了得到更高效的算法，我们需要在子问题之间建立一个简单的递推关系，因此定义一个优化函数

对于数组A=<2,-5,8,11,-3,4,6>，其优化函数为：C[1]=2、C[2]=-3、C[3]=8、C[4]=19、C[5]=16、C[6]=20、C[7]=26

在这种优化函数中，C [ i +1］可以通过 C[ i ] 直接得到，因为如果 A [1... i +1 ］的子段 A [ k .. i +1］是使得 C [ i ＋1 ]达到最大和的子段，那么 A [ k ... i ］一定是使得 C [ i ]达到最大和的子段．如若不然，存在一个使得 C[ i ]达到更大和的子段 A [ t ... i ]，那么在 A [ t ... i ］后面加上 A[ i+1 ]所得到的子段 A [ t ... i +1］之和将大于 C [ i +1].这与 C [ i 十1］是 A [1.. i +1］以元素 A [ i +1］作为最后元素的最大子段和矛盾．这恰好验证了这样定义的优化函数满足优化原则于是，我们在考虑怎样选择才能使得 C [ i +1］达到最大值时，只要考虑一个问题：是否需要把 C [ i ]加到 A [ i +1上？而这取决于 C [ i ]是否大于0．

那么递推关系为：

$C[i+1]=max\left \{ C[i]+A[i+1],A[i+1] \right \} \quad i=1,2,....,n$

$C[1]=A[1] \quad$ 若A[1]>0,否则C[1]=0

根据上面的递推公式，得到C[1]，C[2]，C[3].....C[n，]恰好枚举了以任何元素为最后元素的所有子段的最大和，我们要找到所求问题的最大子段和，就要对上面n个子段和进行比较，找到其中最大和。

伪代码

//MaxSum(A,n) 【动态规划】
//输入：数组A
//输出：最大子段sum，子段的最后位置c

$sum\leftarrow 0$
$b\leftarrow 0$
$for \quad i\leftarrow 1\quad to \quad n \quad do$
       $if \quad b>0$
       $then \quad b\leftarrow b+A[i]$
       $else \quad b\leftarrow A[i]$
       $if \quad b>sum$
       $then \quad sum\leftarrow b$
                    $c\leftarrow i$
$return \quad sum,n$

算法分析

MaxSum(A,n) 算法只有一个for循环，执行次数为O(n)，循环体内都是常数次运算，因此算法复杂度为O(n)

程序

//算法3.10 MaxSum(A,n) 【动态规划】 
//输入：数组A
//输出：最大子段sum，子段的最后位置c#include<stdio.h>
#include<stdlib.h>void MaxSum(int A[], int n)
{int sum = 0;int b = 0;int i,c;for(i = 0;i < n;i++){if(b > 0)b= b+A[i];elseb = A[i];if(b > sum){sum = b;c = i;}}printf("数组A的最大连续子段和为：%d,且子段最后位置为：%d",sum,c+1);
} int main()
{int A[7]={2,-5,8,11,-3,4,6};int i;for(i = 0;i < 7;i++){printf("%d ",A[i]);}printf("\n");MaxSum(A,7); return 0;
}