1、一文看懂 AI 数据集：训练集、验证集、测试集： 

https://zhuanlan.zhihu.com/p/98532085

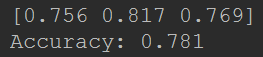
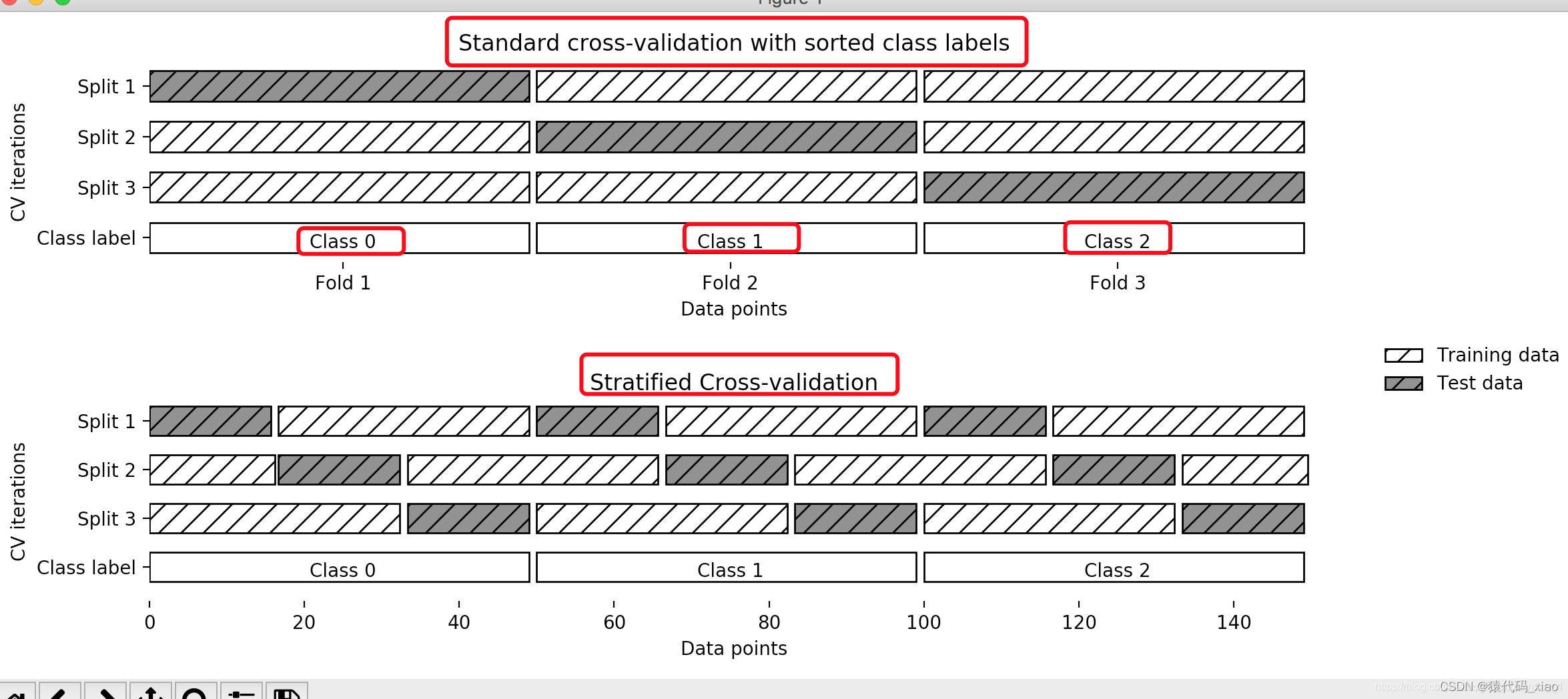
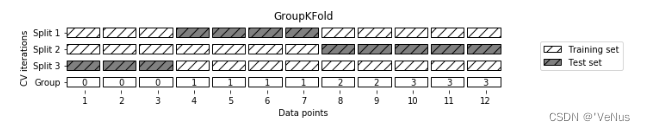
2、机器学习之K折交叉验证 - 吉什么的文章 - 知乎 https://zhuanlan.zhihu.com/p/38121870

注意：cross_val_score() 传入的 X 和 y 是原始特征和标签，而非经过 train/test split 的训练集。

划分过程由 cross_val_score() 函数内完成。

3、Cross-validation: evaluating estimator performance

                                            

                                          

     

训练集

训练集用来训练模型，即确定模型的权重和偏置这些参数，通常我们称这些参数为学习参数。

验证集

而验证集用于模型的选择，更具体地来说，验证集并不参与学习参数的确定，也就是验证集并没有参与梯度下降的过程。验证集只是为了选择超参数，比如网络层数、网络节点数、迭代次数、学习率这些都叫超参数。比如在k-NN算法中，k值就是一个超参数。所以可以使用验证集来求出误差率最小的k。

测试集

测试集只使用一次，即在训练完成后评价最终的模型时使用。它既不参与学习参数过程，也不参数超参数选择过程，而仅仅使用于模型的评价。 
值得注意的是，千万不能在训练过程中使用测试集，而后再用相同的测试集去测试模型。这样做其实是一个cheat，使得模型测试时准确率很高。

                                                           

4、Plotting Cross-Validated Predictions

5、Tuning the hyper-parameters of an estimator

It is possible and recommended to search the hyper-parameter space for the best cross validation score.

scikit-learn中提供了两种对搜索候选对象进行采样的通用方法：对于给定值，GridSearchCV穷举考虑所有参数组合，而RandomizedSearchCV可以从具有指定分布的参数空间中采样给定数量的候选对象。

请注意，通常这些参数的一小部分会对模型的预测或计算性能产生较大影响，而其他参数则可以保留其默认值。建议阅读估计器类的文档字符串，以更好地了解其预期行为，这可能是通过阅读随附的文献参考来实现的。

6、时序问题中的交叉验证怎么做？ - Alex的文章 - 知乎 https://zhuanlan.zhihu.com/p/141542218

7、干货笔记：过拟合处理 - AtomPai的文章 - 知乎 https://zhuanlan.zhihu.com/p/38947625