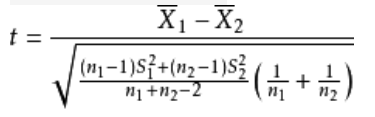1.k-mean算法的原理

1、选取K个点做为初始聚集的簇心

2、分别计算每个样本点到K个簇核心的距离（这里的距离一般取欧氏距离或余弦距离)，找到离该点最近的簇核心，将它归属到对应的簇

3、所有点都归属到簇之后，M个点就分为了K个簇。之后重新计算每个簇的重心（平均距离中心)，将其定为新的“簇核心”;

4、反复迭代2-3步骤，直到达到某个中止条件。
直到质心不再改变

2.聚类算法

聚类算法：是一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。

聚类算法与分类算法最大的区别是：聚类算法是无监督的学习算法，而分类算法属于监督的学习算法，分类是知道结果的。

在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

3.kmeans算法效果衡量标准

3.1 K值确定：

Elbow method就是“肘”方法，对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和，可以想象到这个平方和是会逐渐变小的，直到k==n时平方和为0，因为每个点都是它所在的簇中心本身。但是在这个平方和变化过程中，会出现一个拐点也即“肘”点，下图可以看到下降率突然变缓时即认为是最佳的k值。

肘方法的核心指标是SSE(sum of the squared errors，误差平方和)， Ci是第i个簇，p是Ci中的样本点， mi是Ci的质心（Ci中所有样本的均值）， SSE是所有样本的聚类误差，代表了聚类效果的好坏。

肘方法的核心思想：
随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。

并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，

所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。这也是该方法被称为肘方法的原因。

聚类效果怎么判断？
1、SSE误差平方和越小越好，肘部拐点的地方。
2、也可用轮廓系数表示 系数越大，聚类效果越好，簇与簇之间距离越远

kmeans算法的最大弱点：只能处理球形的簇（理论）

3.2轮廓系数：

（ Silhouette Coefficient）结合了聚类的凝聚度（ Cohesion）和分离度（ Separation），用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。

其中p是某个簇C k 中的样本。即，用X i 到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。