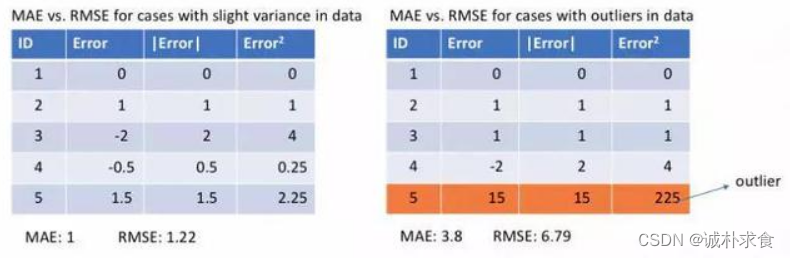
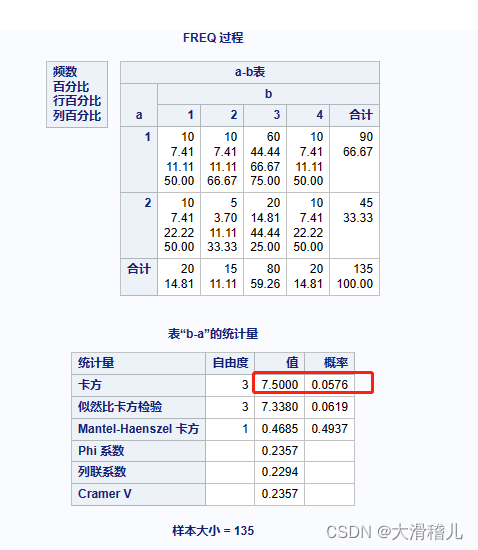
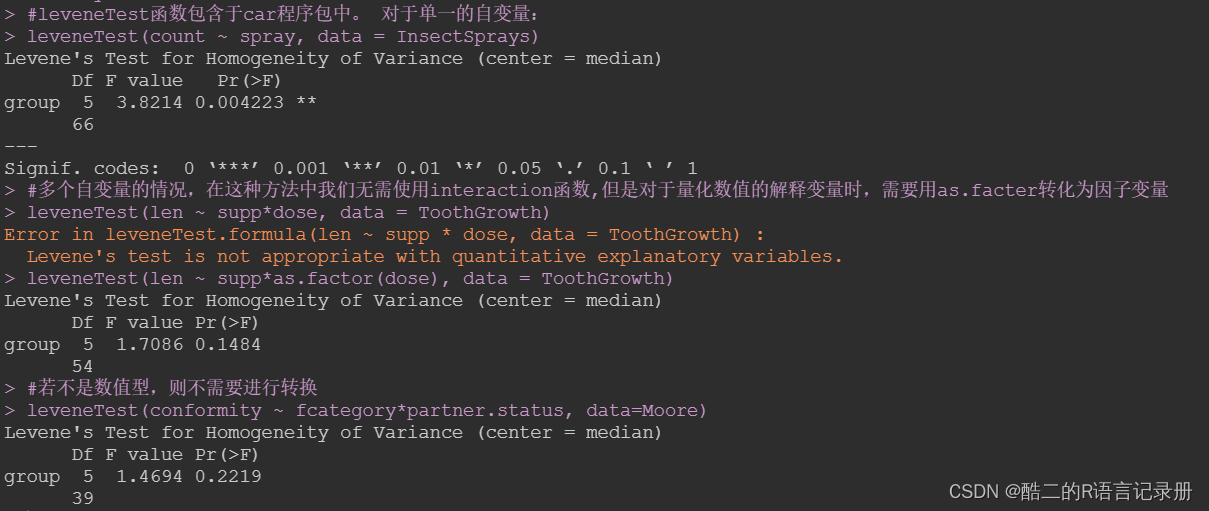
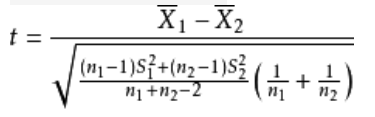目录
- 线性拟合的斜率和截距的不确定性
- Excel数组函数LINEST
- LINEST结果的含义
- LINEST输出的10个统计参数含义如下:
- 模型预测 y ^ \widehat{y} y = m x + b =mx+b =mx+b
- References
线性拟合的斜率和截距的不确定性
利用熟悉的Excel绘图功能,可以根据距离-高程散点数据拟合线性趋势线,如图1显示(河流阶地地形数据)。趋势线按如下方式插入:右击图表上的数据,添加趋势线,在图表上显示方程和 R 2 R^2 R2值。然而,趋势线函数并没有给出与线性拟合的斜率和截距相关的方差值。获得斜率和截距选定的置信区间(例如95%置信区间)对于精确测量断层变形量与滑动速率十分重要。因此,我们需要计算斜率与截距的方差值。Excel的LINESET函数提供这种统计测量。下文介绍了使用LINEST的基本步骤与原理(Morrison, 2014)。

图1. 拔河高度随距离的函数。利用Excel的趋势线特性对数据进行拟合;直线方程和拟合系数R2值如图所示。
Excel数组函数LINEST
使用MS Excel的 LINEST函数 进行最小二乘计算。对于图1所示数据,应用LINEST步骤如下:
- 选择一个5行2列的空白范围(总共10个单元格)来存放函数的输出值;我们选择B1:C5,如图2所示。
- 点击公式,然后 “插入函数”。
- 在 “插入函数” 窗口中,类别选择 “Statistical”,选择函数 “LINEST”,然后单击确定。
- 选择y和x数据范围;对于Const,输入TRUE(TRUE=计算非0截距);对于Stats,也选择TRUE (TRUE=返回误差统计值);单击OK。
- 通过选择输入字段中的公式并按键盘 CTRL-SHIFT-ENTER,指定LINEST是一个数组函数。选定的10个输出单元格将填充与图2和图3中标记的匹配相关的统计信息,下文进行讨论。

图2. 按照文本中的说明,填充LINEST的函数参数,如图所示。点击OK之后,还有最后一个重要的步骤:突出显示函数调用=LINEST(B9:B1493, A9:A1493, true, true)并同时按CTRL-SHIFT-ENTER。

图3. 在指定LINEST是一个数组函数之后,10个单元格B1:C5显示误差统计信息。这些统计值的含义见文本。
LINEST结果的含义
LINEST执行最小二乘运算求解最佳拟合直线的斜率和截距(图4,Wikipedia, 2014b)。最佳线性拟合对应拟合直线和数据之间的平方和误差值最小。通常,最小二乘计算中,假设x值没有误差(图4),详细推导见文献(Montgomery and Runger, 2011; McCuen, 1985),本文仅作简短讨论。

图4. 因变量y的平均值是参数(斜率和截距)和变量x的线性组合。通常最小二乘算法假设数据的x值不存在误差,响应变量y的残差计算为 y i − y ^ i y_i-\widehat{y}_i yi−y i,即点与直线之间的垂直距离(左图)。若x中的误差也存在,点和直线之间的最短距离是垂直距离,如右图所示。各因变量 y i y_i yi的误差是互不相关的,即每个 y i y_i yi之间不存在协方差。
值(xi, yi)是n个数据对的集合,我们希望拟合一条线; y ˉ ≡ ( ∑ i = 1 n y i ) / n \bar{y}≡(\sum_{i=1}^n y_i )/n yˉ≡(∑i=1nyi)/n是yi的均值,并且线性拟合是 y ^ ( x ) = m ^ x + b ^ \widehat{y}(x)=\widehat{m}x+\widehat{b} y (x)=m x+b ,为了解释Excel返回的误差统计值,首先定义三个平方和: S S y y SS_{yy} SSyy, S S E SS_E SSE, 和 S S R SS_R SSR
总平方和 S S T SS_T SST= S S y y SS_{yy} SSyy= ∑ i = 1 n ( y i − y ˉ ) 2 \sum\limits_{i=1}^n(y_i-\bar{y})^2 i=1∑n(yi−yˉ)2 (1)
误差平方和 S S E SS_E SSE≡ ∑ i = 1 n ( y i − y ^ ) 2 \sum\limits_{i=1}^n(y_i-\widehat{y})^2 i=1∑n(yi−y )2 (2)
回归平方和 S S R SS_R SSR≡ S S T − S S E SS_T-SS_E SST−SSE (3)
S S y y SS_{yy} SSyy是数据 y i y_i yi与均值 y ^ \widehat{y} y 之间误差平方和; S S E SS_E SSE是数据 y i y_i yi和拟合值 y ^ ( x ) \widehat{y}(x) y (x)= m ^ x + b ^ \widehat{m}x+\widehat{b} m x+b 之间的误差平方和; S S R SS_R SSR是二者之差,代表总平方和中可以用线性模型值解释的部分。在最小二乘计算中,目标是找到最小化的 S S E SS_E SSE,计算过程还涉及到两个平方和公式:
S S x x SS_{xx} SSxx≡ ∑ i = 1 n ( x i − x ˉ ) 2 \sum\limits_{i=1}^n(x_i-\bar{x})^2 i=1∑n(xi−xˉ)2 (4)
S S x y SS_{xy} SSxy≡ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) \sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) i=1∑n(xi−xˉ)(yi−yˉ) (5)
其中 x ˉ \bar{x} xˉ≡ ( ∑ i = 1 n x i ) / n (\sum_{i=1}^nx_i )/n (∑i=1nxi)/n是 x i x_i xi的平均值。
将n个数据点( x i x_i xi, y i y_i yi)拟合的线性模型:
y ^ ( x ) = m ^ x + b ^ \widehat{y}(x)=\widehat{m}x+\widehat{b} y (x)=m x+b (6)
LINEST输出的10个统计参数含义如下:
-
m,斜率的最小二乘估计值——通常为最佳拟合直线的斜率。
m ^ \widehat{m} m = ( n ∑ i = 1 n x i y i − ( ∑ i = 1 n x i ) ( ∑ i = 1 n y i ) ( n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 ) \frac{(n\sum_{i=1}^nx_i y_i-(\sum_{i=1}^nx_i)(\sum_{i=1}^ny_i)}{(n\sum_{i=1}^nx_i^2-(\sum_{i=1}^nx_i)^2 )} (n∑i=1nxi2−(∑i=1nxi)2)(n∑i=1nxiyi−(∑i=1nxi)(∑i=1nyi)= ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − y ˉ ) 2 \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(x_i-\bar{y})^2} ∑i=1n(xi−yˉ)2∑i=1n(xi−xˉ)(yi−yˉ)= S S x y S S x x \frac{SS_{xy}}{SS_{xx}} SSxxSSxy (7) -
b,截距的最小二乘估计值——通常为最佳拟合直线的截距。
b ^ \widehat{b} b = ( ∑ i = 1 n x i ) 2 ( ∑ i = 1 n y i ) − ( ∑ i = 1 n x i y i ) ( ∑ i = 1 n x i ) ( n ∑ i = 1 n x i 2 − ( ∑ i = 1 n x i ) 2 ) \frac{(\sum_{i=1}^nx_i )^2 (\sum_{i=1}^ny_i)-(\sum_{i=1}^nx_iy_i)(\sum_{i=1}^nx_i)}{(n\sum_{i=1}^nx_i^2 -(\sum_{i=1}^nx_i)^2)} (n∑i=1nxi2−(∑i=1nxi)2)(∑i=1nxi)2(∑i=1nyi)−(∑i=1nxiyi)(∑i=1nxi)= y ˉ − m ^ x ˉ \bar{y}-\widehat{m}\bar{x} yˉ−m xˉ (8) -
n-p, 最小二乘回归自由度。有n个数据点,p = 2个回归参数(m和b)。在进行最小二乘计算之前,有n个自由度,计算斜率和截距时使用了两个自由度,在以后的计算中留下n-2个自由度。
-
S y , x S_{y,x} Sy,x,y(x)的标准偏差(y(x)方差 S y , x 2 S_{y,x}^2 Sy,x2的平方根):
S y , x 2 S_{y,x}^2 Sy,x2= ( 1 n − 2 ) ∑ i = 1 n ( y i − y ^ ) 2 (\frac{1}{n-2})\sum_{i=1}^n(y_i-\widehat{y})^2 (n−21)∑i=1n(yi−y )2= S S E n − 2 \frac{SS_E}{n-2} n−2SSE (9) -
S m S_m Sm,坡度 m ^ \widehat{m} m 标准差( S m 2 S_m^2 Sm2的平方根,m ̂的方差)。
S m 2 S_m^2 Sm2= S ( y , x ) 2 S S x x \frac{S_(y,x)^2}{SS_{xx}} SSxxS(y,x)2 (10)
其中 S y , x 2 S_{y,x}^2 Sy,x2是y(x)的方差(见方程9)。为了求得计算的\widehat{m}和\widehat{b}的置信区间,我们采用t分布和n-2自由度(Montgomery and Runger, 2011)。对于自由度大于或等于6, t α / 2 , n − 2 ≥ 6 ≈ 2 t_{α/2,n-2≥6}≈2 tα/2,n−2≥6≈2(α=0.05,误差为一个有效数字)。
坡度95%置信区间(α=0.05): m ^ ± t 0.025 , n − 2 S m \widehat{m}±t_{0.025,n-2}S_m m ±t0.025,n−2Sm (11)
≅ m ^ ± 2 S m \widehat{m}±2S_m m ±2Sm, ( n − 2 ) ≥ 6 (n-2)≥6 (n−2)≥6 (12) -
S b S_b Sb,截距b ̂的标准差( S b 2 S_b^2 Sb2的平方根,\widehat{b}的方差)。\widehat{b}的置信区间由 S b S_b Sb和具有n-2自由度的t分布获得。
S b 2 S_b^2 Sb2= S y , x 2 ∑ i = 1 n x i 2 n S S x x \frac{S_{y,x}^2 \sum_{i=1}^nx_i^2}{nSS_{xx}} nSSxxSy,x2∑i=1nxi2= S y , x 2 ( 1 n + x ˉ 2 S S ) S_{y,x}^2(\frac1n+\frac{\bar{x}^2}{SS}) Sy,x2(n1+SSxˉ2) (13)
截距95%置信区间(α=0.05): b ^ ± t 0.025 , n − 2 S b \widehat{b}±t_{0.025,n-2}S_b b ±t0.025,n−2Sb (14)
≅ m ^ ± 2 S b \widehat{m}±2S_b m ±2Sb, ( n − 2 ) ≥ 6 (n-2)≥6 (n−2)≥6 (15) -
误差的残差平方和 S S E SS_E SSE——数据 y i y_i yi和线性模拟值 y ^ i \widehat{y}_i y i之差的平方和;一种线性模型y数据的误差度量。当 S S E SS_E SSE→0时,所有的总误差 S S T SS_T SST都可以用线性模型来解释,可以认为线性模型是一个很好的拟合(方程2)。
S S E SS_E SSE≡ ∑ i = 1 n ( y i − y ^ ) 2 \sum\limits_{i=1}^n(y_i-\widehat{y})^2 i=1∑n(yi−y )2 (2) -
回归平方和 S S R SS_R SSR——总平方和中可以用线性模型值解释的部分(方程3):
S S R SS_R SSR≡ S S T − S S E SS_T-SS_E SST−SSE (3) -
R 2 R^2 R2决定系数——线性模型解释的 y i y_i yi变量分数:
R 2 R^2 R2= e x p l a i n e d e r r o r t o t a l e r r o r \frac{explained error}{total error} totalerrorexplainederror= S S R S S T \frac{SS_R}{SS_T} SSTSSR= S S T − S S E S S T \frac{SS_T-SS_E}{SS_T} SSTSST−SSE
当线性模型拟合很好时,数据 y i y_i yi与模型之间的偏差很小, S S E SS_E SSE→0, R 2 R^2 R2=1。因此,决定系数是一种拟合优度的度量,该值越接近1,表明拟合的越好。但是,当拟合模型是一条水平线时,即 y ^ \widehat{y} y = y ^ \widehat{y} y ,则 S S T SS_T SST= S S E SS_E SSE,此时 R 2 R^2 R2为0。 -
Fisher F 统计——用于回归测试,以查看使用两个参数(斜率和截距)是否优于使用一个参数( y ^ \widehat{y} y = y ^ \widehat{y} y ;即坡度m为0,y=截距b)。回归统计F计算为两个量的比率,即模型能够解释的方差与模型不能解释的方差的比率:
F= ( ′ l a c k o f f i t ′ s u m o f s q u a r e s / v 1 ) ′ p u r e e r r o r ′ s u m o f s q u a r e s ) / v 2 (\frac{'lack of fit' sum of squares/v_1)}{'pure error' sum of squares)/v_2} (′pureerror′sumofsquares)/v2′lackoffit′sumofsquares/v1)= S S R / v 1 S S T / v 2 \frac{SS_R/v_1}{SS_T/v_2} SST/v2SSR/v1= S S T − S S E S y , x 2 \frac{SS_T-SS_E}{S_{y,x}^2} Sy,x2SST−SSE
其中 v 1 v_1 v1=1和 v 1 v_1 v1=n-2是每个变量的自由度。这个比率是一个具有F( v 1 v_1 v1, v 2 v_2 v2)分布且自由度为 v 1 v_1 v1=1和 v 1 v_1 v1=n-2的随机变量的计算值。如果F> F c r i t F_crit Fcrit,使用线性模型 y ^ = m ^ x + b ^ \widehat{y}=\widehat{m}x+\widehat{b} y =m x+b 比使用模型 y ^ \widehat{y} y = y ˉ \bar{y} yˉ合理(在(1-α)%置信区间)。 F c r i t F_crit Fcrit对应于具有期望的α置信水平的F( v 1 v_1 v1, v 2 v_2 v2)分布的累积分布函数,自由度为 v 1 v_1 v1和 v 2 v_2 v2。
模型预测 y ^ \widehat{y} y = m x + b =mx+b =mx+b
在方程12和15中,我们给出了两个模型参数 m ^ \widehat{m} m 和 b ^ \widehat{b} b 的95%置信区间。当模型参数 m ^ \widehat{m} m 和 b ^ \widehat{b} b 直接用于后续的计算时,这些置信区间适用于误差传播计算。
当模型方程用于在选定的x值处估计y值时,具有不同的误差范围。这里讨论最常见的情况。
用选定的x值估计最佳y值。任意点上y的最佳值是该点上y所有可能观测值的均值。设x的取值为 x p x_p xp, x在该点的最佳估计值为 y p y_p yp,由下式给出:
y p = m ^ x p + b ^ y_p=\widehat{m}x_p+\widehat{b} yp=m xp+b (18)
y p y_p yp的方差由方程18和误差传播计算而来,斜率和截距不是独立的变量增加了其复杂性,因此 m ^ \widehat{m} m 和 b ^ \widehat{b} b 之间的协方差非零。y在 x p x_p xp处的均值方差为:
y在 x p x_p xp的均值方差: S y , x 2 ( 1 n + ( x p − x ˉ ) 2 S S x x ) S_{y,x}^2(\frac1n+\frac{(x_p-\bar{x})^2}{SS_{xx}}) Sy,x2(n1+SSxx(xp−xˉ)2) (19)
y在y_p处的均值置信区间根据符合t分布且自由度为(n-2)的标准差得到(Montgomery and Runger, 2011):
y在 x p x_p xp的均值置信区间:
( m ^ x p + b ^ ) ± t ( α / 2 , n − 2 ≥ 6 ) s y , x 1 n + ( x p − x ˉ ) 2 S S x x (\widehat{m}x_p+\widehat{b})±t_{(α/2,n-2≥6)} s_{y,x}\sqrt{{\frac1n}+\frac{(x_p-\bar{x})^2}{SS_{xx}}} (m xp+b )±t(α/2,n−2≥6)sy,xn1+SSxx(xp−xˉ)2 (20)
方程20是基于最小二乘法最佳拟合得到的y值误差的合理区间(图5)。由此可知。误差条在回归( x ˉ \bar{x} xˉ, y ˉ \bar{y} yˉ)的中心点附近最窄,并向两端呈扇形展开。这反映了这样一个事实,即斜率的不确定性使得x范围两端的值不如中心附近的点确定。

图5. 图1中数据的拟合线(红色)与95%置信区间。外层的一对线(绿色和紫色)反映了在每个x值处y新值的95%预测区间。
References
[1]: D. C. Montgomery and G. C. Runger., 2011. Applied Statistics and Probability for Engineers, 5th edition (Wiley, New York).
[2]: Morrison, F. A., 2014. Obtaining uncertainty measures on slope and intercept of a least squares fit with Excel’s LINEST. Houghton, MI: Department of Chemical Engineering, Michigan Technological University. Retrieved August, 2014, 6: 2015.
[3]: R. H. McCuen., 1985. Statistical Methods for Engineers (Prentice Hall, Englewood Cliffs, NJ).
[4]: Wikipedia., 2014. “Ordinary Least Squares,” Wikipedia, the Free Encyclopedia, en.wikipedia.org/wiki/Ordinary_least_squares, accessed 14 July 2014.