回归分析(regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;
按照因变量的多少,可分为简单回归分析和多重回归分析;
按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
非线性拟合
离散参数非线性拟合的基本方法:
① 获得离散点数据;
② 确定函数模型,即确定想要拟合关联式的形式;
③ 确定选用函数模型中的未知参数
④ 即可确定拟合函数的具体形式
⑤ 还可画出拟合曲线
多元非线性拟合,依托nlinfit函数

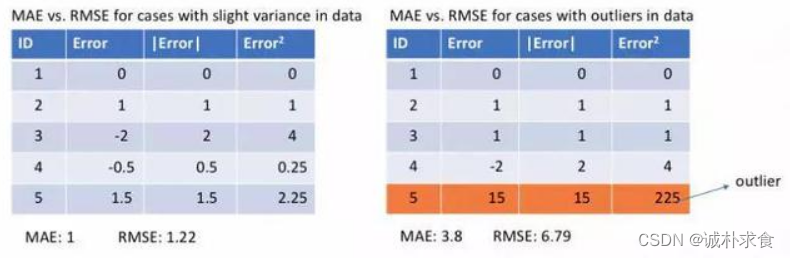
和方差(SSE)和均方差(MSE):其中MSE=SSE/n,SSE表示的是拟合数据和原始数据对应点的误差的平方和,其越接近0,说明模型选择和拟合更好,数据预测也越成功。
残差:真实值和估计值之间的差。
确定系数(R-square):通过数据的变化来表征一个拟合的好坏,其范围为{0,1},越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也越好。
实例1—一元非线性拟合
① 使用MATLAB
X=2:16;
Y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
mymodel=inline('beta(1)*exp(beta(2)./X)','beta','X');
beta0 = [1, 1]; % 初值的选取可能会导致结果具有较大的误差
beta=nlinfit(X,Y,mymodel,beta0);
结果:
beta=11.6036
-1.0641
其中初值的选择会影响最终的拟合结果,不同的初值最终拟合出来的拟合参数是不一样的,即不同的初值会拟合出“一套”对应的拟合参数,这一套拟合参数会得到精确的结果。
但是在拟合过程中,MATLAB会发出Warning,提示,拟合出来的公式预测结果不可靠。但是在本人经过多次尝试下,发现拟合出来的结果还行,因此后续在使用这个拟合公式时,可以通过校核数据的方法来进行校核,这样确保拟合公式的准确性。
② 使用1stopt软件
Parameter b1, b2; //拟合参数
Variable x,y; // 变量
Function y=b1*exp(b2/x);//数学模型
Data;//数据
2 6.42
3 8.20
4 9.58
5 9.5
6 9.7
7 10
8 9.93
9 9.99
10 10.49
11 10.59
12 10.60
13 10.80
14 10.60
15 10.90
16 10.76
计算结果:
b1=11.6036;
b2=-1.0641;
相比于MATLAB,1stopt软件中的非线性拟合功能,最大的好处就是摆脱了初值的影响,因为其根本不需要初值,据说其开发了一套独一无二的全局性优化算法,很好地解决了MATLAB存在的这一最大的局限。
当然该软件的使用方法极其简单,非常容易掌握。
但是非常遗憾,这个软件很难在网上找得到免费版,能找到的极限也就是有参数限制(四个拟合参数限制)的试用版,后面也询问了该公式的价格,几千元左右吧。对于学生来说,还是蛮贵的。
本人这里只有一个四参数试用版,如果有同学愿意学习一下,烦请发送邮件至3453126994@qq.com。(本人也是得到网络前辈的照顾,将之传递下去,不存在任何利益,如果有侵权,立马删除。)
实例2—多元非线性拟合
多元非线性拟合,依托lsqcurvefit函数
格式:lsqcurvefit(f,a,x,y)
f: 符号函数句柄,如果是以m文件的形式调用的时候,别忘记加@.这里需要注意,f函数的返回值是和y匹对的,即拟合参数的标准是(f-y)^2取最小值,具体看下面的例子
a:最开始预估的值(预拟合的未知参数的估计值)。如上面的问题如果我们预估A为1,B为2,C为3,则a=[1 2 3]
x:我们已经获知的x的值
y:我们已经获知的x对应的y的值
xdata=[950;1150;1350];
ydata=[200;100;50];
fun1 = @(x,xdata)x(1)+x(2)*exp(-(xdata./x(3)).^2); %自定义函数类型
X0=[0,1120,740]; %初始参数
[X,resnorm]=lsqcurvefit(fun1,X0,xdata,ydata); %resnorm残差平方和 X是参数
disp(X) %得到所求参数
注意:因为初值对拟合速度甚至结果有一定的影响。在确定数学模型后,拟合非线性问题时,初值应该如何选取呢?
①如果已知数学模型,有一定物理意义,则建议根据物理意思选取;
②当无法确定初值时,且你的数学模型有导数(如果求导模型很复杂甚至没有导数,则可进行简单的差分构造),则可以采取如下的办法进行:
1)求出拟合函数的一阶导数;
2)使用已知数据求出近似点的一阶导数;
3)代入一阶导数函数以及原函数求得初值近似值。