概述Holdout 交叉验证K-Fold 交叉验证Leave-P-Out 交叉验证总结

概述

交叉验证是在机器学习建立模型和验证模型参数时常用的办法。

顾名思义，就是重复的使用数据，把得到的样本数据进行切分，组合为不同的训练集和测试集。

用训练集来训练模型，用测试集来评估模型预测的好坏。

在此基础上可以得到多组不同的训练集和测试集，某次训练集中的某样本在下次可能成为测试集中的样本，即所谓“交叉”。

下面我们将讲解几种不同的交叉验证的方法。

Holdout 交叉验证

Holdout 交叉验证就是将原始的数据集随机分成两组，一组为测试集，一组作为训练集。

我们使用训练集对模型进行训练，再使用测试集对模型进行测试。

记录最后的模型准确度作为衡量模型性能的指标。

这是最简单的交叉验证的方法，当我们需要针对大量数据进行简单快速的验证时，Holdout 验证是一个不错的方法。

通常，Holdout 交叉验证会将数据集的20%——30%作为测试集，而其余的数据作为训练集。

当测试集的占比较高的时候，会导致训练的数据不足，模型较为容易出错，准确度较低。

当测试集的占比较低的时候，会导致训练的数据过多，模型可能会出现过拟合或者欠拟合的问题。

#以下是Holdout 交叉验证的示例代码#导入包，使用sklearn进行交叉验证
import pandas
from sklearn import datasets
from sklearn.model_selection import train_test_split#将训练集的比例设为70%，测试集的比例设为30%
#可以通过更改这个数值来改变训练集的比例
TRAIN_SPLIT = 0.7#设置以下diabetes数据集的列名
columns = ['age', 'sex', 'bmi', 'map', 'tc', 'ldl', 'hdl', 'tch', 'ltg', 'glu'
]#导入diabetes数据集
dataset = datasets.load_diabetes()#创建数据集的dataframe
dataframe = pandas.DataFrame(dataset.data, columns=columns)#看下数据集基本情况
dataframe.head()#使用train_test_split对数据集进行分割

#train_test_split 是sklearn中分割数据集的常用方法
#train_size 设置了训练集的比例x_train, x_test, y_train, y_test = train_test_split(dataframe, dataset.target, train_size=TRAIN_SPLIT, test_size=1-TRAIN_SPLIT)#看下数据集的条数
print("完整数据集的条数: {}".format(len(dataframe.index)))#看下训练集和测试集的数据占比
print("训练集的条数（占比）: {} (~{}%)".format(len(x_train), TRAIN_SPLIT*100))
print("测试集的条数（占比）: {} (~{}%)\n".format(len(x_test), (1-TRAIN_SPLIT)*100))#下面两行代码可以看下具体的数据明细，取消注释即可
# print("Training data:\n{}\n".format(x_train))
# print("Test data:\n{}".format(x_test))

完整数据集的条数: 442
训练集的条数（占比）: 309 (~70.0%)
测试集的条数（占比）: 133 (~30.000000000000004%)

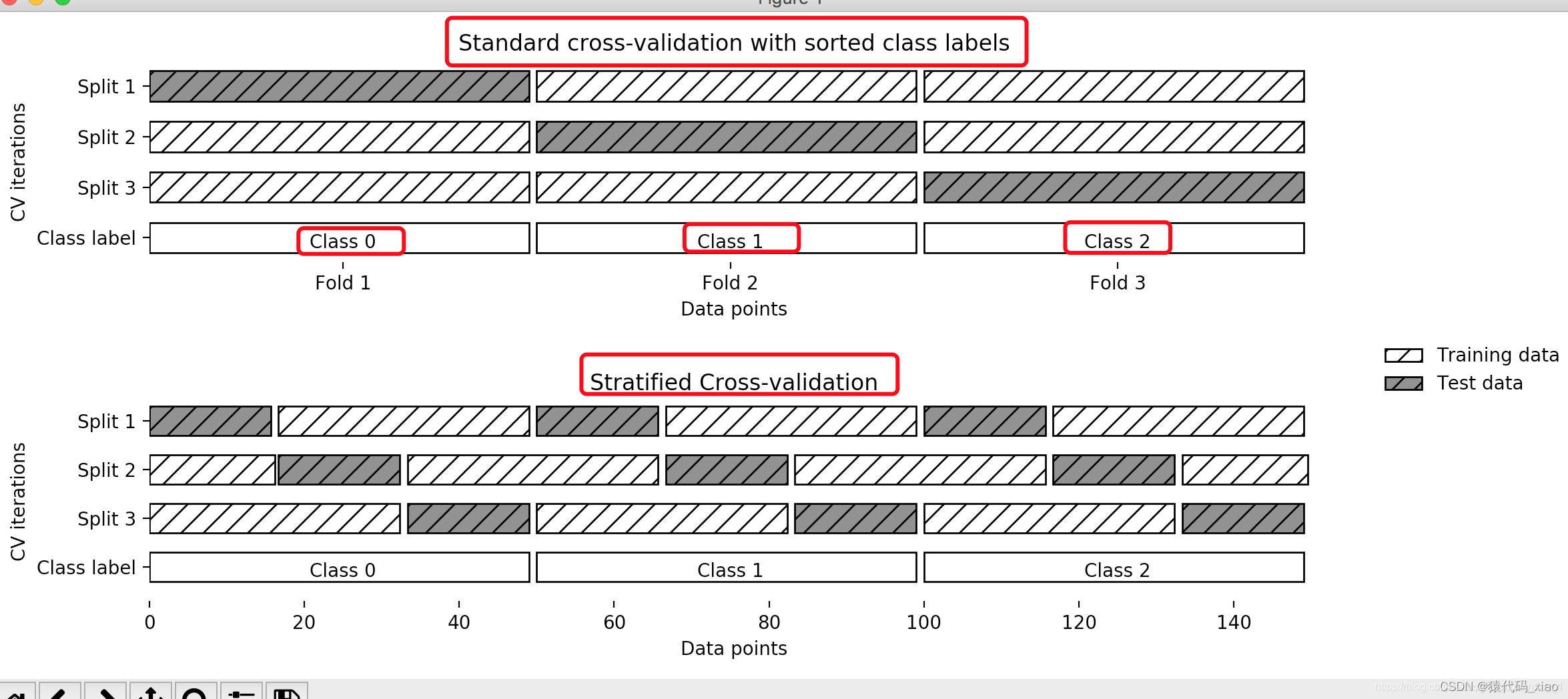
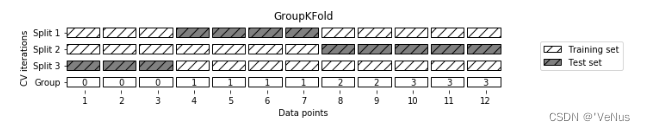
K-Fold 交叉验证

K-Fold 交叉验证会将数据集分成K个部分，其中一个单独的样本作为测试集，而其余K-1个样本作为训练集。

交叉重复验证K次，每个子集都会作为测试集，对模型进行测试。

最终平均K次所得到的结果，最终得出一个单一的模型。

假如我们有100个数据点，并且分成十次交叉验证。

那么我们会将数据分成十个部分，每个部分有十个数据点。

我们可以分别对十个数据点进行验证，而对使用另外的90个数据点进行训练。

重复十次这样的操作，将得到十个模型。

我们对这些模型进行平均，最终得出一个适合的模型。

K-Fold 交叉验证适用于数据集样本比较小的情况。

#以下是K-Fold 交叉验证的示例代码
#导入相关的包
import numpy
#从sklearn中导入KFold
from sklearn.model_selection import KFold#设置K值为3
NUM_SPLITS = 3#创建一个数据集方便使用KFold Cross Validation
data = numpy.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10], [11, 12]])#看下数据情况
data

array([[ 1,  2],[ 3,  4],[ 5,  6],[ 7,  8],[ 9, 10],[11, 12]])

#导入kfold交叉验证，将K值设置为3
kfold = KFold(n_splits=NUM_SPLITS)
#使用kfold分割数据
split_data = kfold.split(data)

#使用循环分别导出三次KFOLd的情况下训练集和测试集的数据内容
#将训练集设置为— 测试集设置为T#使用for循环
for train, test in split_data:#初始输出设置为空output_train = ''output_test = ''#初始case设置为—bar = ["-"] * (len(train) + len(test))#创建子循环for i in train:#输出训练集的内容以及训练集的数据编号output_train = "{}({}: {}) ".format(output_train, i, data[i])for i in test:#将测试集的case改成Tbar[i] = "T"#输出测试集的内容以及测试集的数据编号output_test = "{}({}: {}) ".format(output_test, i, data[i])#训练集和测试集的直观标志print("[ {} ]".format(" ".join(bar)))print("训练集: {}".format(output_train))print("测试集:  {}\n".format(output_test))

[ T T - - - - ]
训练集: (2: [5 6]) (3: [7 8]) (4: [ 9 10]) (5: [11 12]) 
测试集:  (0: [1 2]) (1: [3 4]) [ - - T T - - ]
训练集: (0: [1 2]) (1: [3 4]) (4: [ 9 10]) (5: [11 12]) 
测试集:  (2: [5 6]) (3: [7 8]) [ - - - - T T ]
训练集: (0: [1 2]) (1: [3 4]) (2: [5 6]) (3: [7 8]) 
测试集:  (4: [ 9 10]) (5: [11 12]) 

Leave-P-Out 交叉验证

Leave-P-Out 交叉验证（LPOCV）使用样本中的某几项当做测试集，从样本中选取某几项的可能种类称为P值。

举个例子，当我们有四个数据点，而我们要将其中的两个数据点当做测试集。

则我们一共有   种可能性，直观的展现如下所示：（T代表测试集，—代表训练集）

1: [ T T - - ]
2: [ T - T - ]
3: [ T - - T ]
4: [ - T T - ]
5: [ - T - T ]
6: [ - - T T ]

下面是LPOCV的另外一种可视化：

LPOCV可以迅速提高模型的精确度，准确的描摹大样本数据集的特征信息。

模型使用LPOCV的迭代次数可以用   来计算。

其中N代表数据点的个数，而P代表了测试集数据点的个数。

例如我们有十个数据点，所选测试集数据点为三个。

那么LPOCV将迭代   次。

LPOCV的一个极端案例是LOOCV（ Leave-One-Out Cross Validation）。

LOOCV限定了P的值等于1，这使得我们将迭代N次来评估模型。

LOOCV也可以看做是KFold交叉验证，其中   

与KFold类似，LPOCV和LOOCV都可以遍历整个数据集。

因此，针对于小型的数据集，LPOCV和LOOCV十分有效。

#以下是LPOCV、LOOCV的示例代码
#导入包
import numpy
#从sklearn中导入LPOCV，LOOCV
from sklearn.model_selection import LeaveOneOut, LeavePOut#设置P值等于2
P_VAL = 2#定义一个导出分割数据的函数
def print_result(split_data):for train, test in split_data:#初始输出设置为空output_train = ''output_test = ''#初始case设置为—bar = ["-"] * (len(train) + len(test))#创建子循环for i in train:#输出训练集的内容以及训练集的数据编号output_train = "{}({}: {}) ".format(output_train, i, data[i])for i in test:#将测试集的case改成Tbar[i] = "T"#输出测试集的内容以及测试集的数据编号output_test = "{}({}: {}) ".format(output_test, i, data[i])#训练集和测试集的直观标志print("[ {} ]".format(" ".join(bar)))print("训练集: {}".format(output_train))print("测试集:  {}\n".format(output_test))#创建一个需要分割的数据集
data = numpy.array([[1, 2], [3, 4], [5, 6], [7, 8]])#分别导入LOOCV个LPOCV模型
loocv = LeaveOneOut()
lpocv = LeavePOut(p=P_VAL)#分别使用LOOCV和LPOCV来分割数据
split_loocv = loocv.split(data)
split_lpocv = lpocv.split(data)#分别输出LOOCV和LPOCV所对应的分割数据
print("LOOCV:\n")
print_result(split_loocv)print("LPOCV (where p = {}):\n".format(P_VAL))
print_result(split_lpocv)

LOOCV:[ T - - - ]
训练集: (1: [3 4]) (2: [5 6]) (3: [7 8]) 
测试集:  (0: [1 2]) [ - T - - ]
训练集: (0: [1 2]) (2: [5 6]) (3: [7 8]) 
测试集:  (1: [3 4]) [ - - T - ]
训练集: (0: [1 2]) (1: [3 4]) (3: [7 8]) 
测试集:  (2: [5 6]) [ - - - T ]
训练集: (0: [1 2]) (1: [3 4]) (2: [5 6]) 
测试集:  (3: [7 8]) LPOCV (where p = 2):[ T T - - ]
训练集: (2: [5 6]) (3: [7 8]) 
测试集:  (0: [1 2]) (1: [3 4]) [ T - T - ]
训练集: (1: [3 4]) (3: [7 8]) 
测试集:  (0: [1 2]) (2: [5 6]) [ T - - T ]
训练集: (1: [3 4]) (2: [5 6]) 
测试集:  (0: [1 2]) (3: [7 8]) [ - T T - ]
训练集: (0: [1 2]) (3: [7 8]) 
测试集:  (1: [3 4]) (2: [5 6]) [ - T - T ]
训练集: (0: [1 2]) (2: [5 6]) 
测试集:  (1: [3 4]) (3: [7 8]) [ - - T T ]
训练集: (0: [1 2]) (1: [3 4]) 
测试集:  (2: [5 6]) (3: [7 8]) 

总结

• Holdout 交叉验证：按照一定比例将数据集拆分为训练集和测试集

• K-Fold 交叉验证：将数据分为K个部分，每个部分分别当做测试集

• Leave-P-Out 交叉验证: 使用P种选择的   可能性分别测试

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：
（1）点击页面最上方“小詹学Python”，进入公众号主页。
（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。
感谢支持，比心。
Avengers小詹开通了一个视频号，会分享互联网那些事、读书心得与副业经验，欢迎各位扫描下方二维码关注。