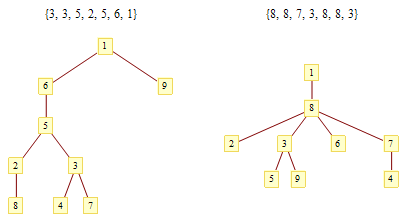
图论

结论：
1.无向完全图：在顶点数给定为n的情况下，边数达到最大的n(n-1)/2条边。
2.有向完全图：在顶点数给定为n的情况下，有向边数达到最大的n(n-1)条边。
3.树是图的特例：无环的无向图
4.生成树有可能不唯一
5.无向连通图所有顶点的度之和为偶数。
6. 有n个顶点的强连通图最多有n(n-1)条边,最少有n条边。
7. 有n个顶点的非连通的无向图，最多有(n-1)(n-2)/2条边
8.用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。
9.如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有两个连通分量。
10.如果e是有权无向图G唯一的一条最短边，那么边e一定会在该图的最小生成树上。
11.若图采用邻接矩阵表示，如果该矩阵不全为0，且矩阵主对角线以下全是0，那么说明该图一定是有向图
12.无向连通图构成的条件是：边数=顶点数-1
13.无向图的邻接矩阵是对称矩阵
14.任何一个无向连通图的最小生成树有一棵或多棵
15.图的BFS生成树的树高比DFS生成树的树高小或相等
16.拓扑排序的图为有向无环图
17.图的广度优先遍历类似于二叉树的层次遍历
18.二叉树一定是有序树

一些概念

：
1.无向图的极大连通子图称为“连通分量
连通分量的概念包含以下4个要点：
子图、连通、极大顶点数、极大边数
2.有向图中任意一对顶点vi 和vj (i≠j)均既有从vi到vj的路径，也有从vj到vi的路径，则称该有向图是“强连通图
3.生成树：图的包含其全部n 个顶点的一个极小连通子图。它必定包含且仅包含G的n-1条边。
4.最小顶点覆盖集：在所有的顶点覆盖集中，顶点数最小的那个叫最小顶点集合
顶点覆盖：
在顶点集合中，选取一部分顶点，这些顶点能够把所有的边都覆盖了。这些点就是顶点覆盖集
5.拓扑序列：用有向无环图中各顶点构成的有序序列
6.强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通
例题
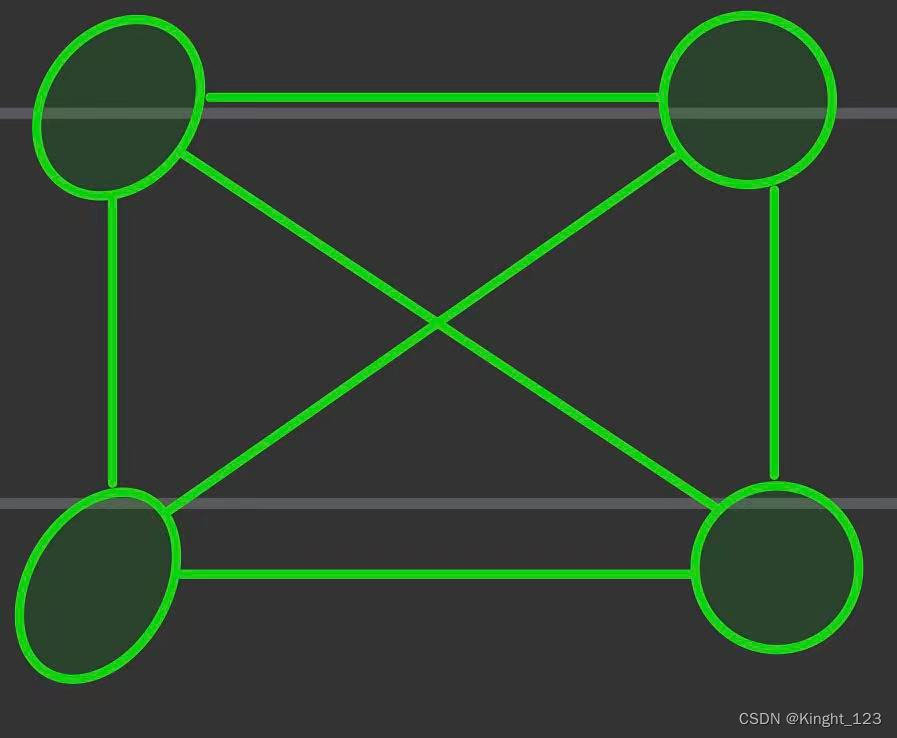
1.用一维数组G[]存储有4个顶点的无向图如下：

G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。


2.如果G是一个有28条边的非连通无向图，那么该图顶点个数最少为多少 9

解：n个顶点 最多拥有 n(n-1)/2条边，所以8个顶点最多有28条边，要想28条边而且保持非连通，至少要9个节点，第九个节点是孤立的，不与任何节点连通。

3.对于给定的有权无向图G，下列哪个说法是正确的？
（）
A.G的最小生成树中，任意一对顶点间的路径必是它们在G中的最短路径
B.设顶点V到W的最短路径为P。若我们将G中每条边的权重都加1，则P一定仍然是V到W的最短路径
C.单源最短路问题可以用O(∣E∣+∣V∣)的时间解决
D.以上都不对