💟作者简介：大家好呀！我是路遥叶子，大家可以叫我叶子哦！❣️
📝个人主页：【路遥叶子的博客】
🏆博主信息：四季轮换叶，一路招摇胜！

专栏

【安利Java零基础】

【数据结构-Java语言描述】

🐋希望大家多多支持😘一起进步呀！~❤️
🌈若有帮助，还请【关注➕点赞➕收藏】，不行的话我再努力努力呀！💪
————————————————
🍁想寻找共同成长的小伙伴，请点击【Java全栈开发社区】

前言

提起数据结构，大家最熟悉的恐怕就是数组、链表、二叉树。而对于“图”这种数据结构，很多人只停留在“听说过”阶段。但是，图也是一种非常重要，而且跟现实息息相关的数据结构。

比如，我们在使用百度、高德地图做导航的时候，城市的地图就是一种图结构；当我们用微信、QQ等社交软件的时候，我们的好友关系网也是一种图结构。

图，是一种比树更为复杂的数据结构，树的节点之间是一对多的关系，并且存在父与子的层级划分，而图的顶点（注意在此不叫节点）之间是多对多的关系，并且所有顶点都是平等的，无所谓谁是父谁是子。

举个例子，微信中许许多多的用户组成了一个多对多的朋友关系网，这个关系网就是数据结构中的图(Graph)。

让我们来详细了解一下图的底蕴吧！

💚❤️💙💚❤❤️💙💚❤️❤💙💚❤️💙❤💚❤️💙💚❤❤️💙💚❤️❤💙❤️💙💚❤

🐋基本概念

❣️❣️什么是图？

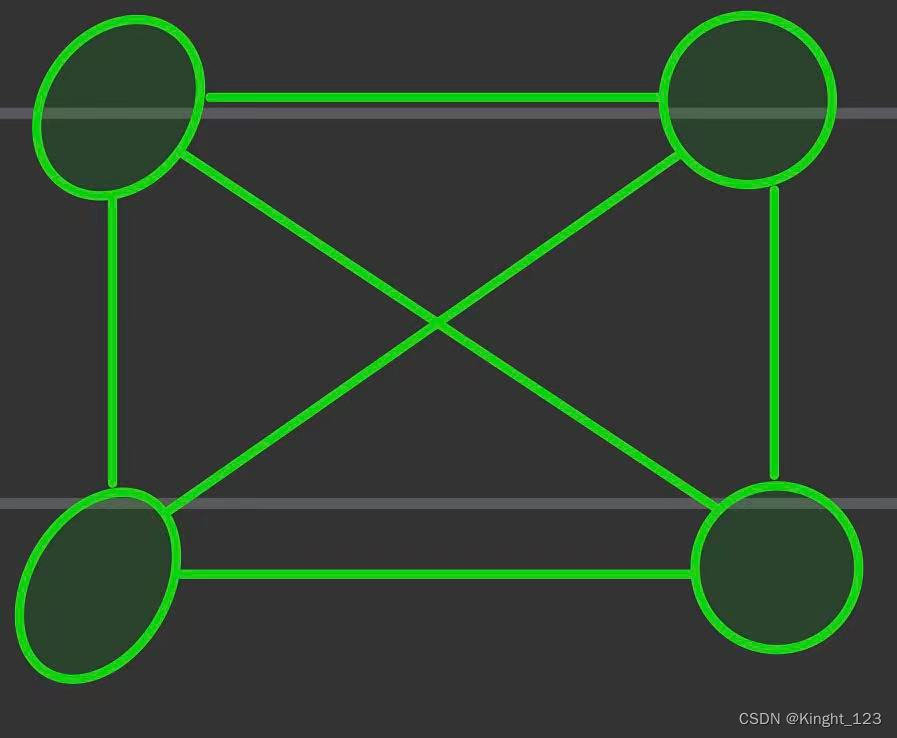
图，是一种用节点和边来表示相互关系的数学模型。

简单的说，点用边连起来就叫做图，严格意义上讲，图是一种数据结构，通常表示为：G＝（v，E），其中，G表示一个图，v是图G中顶点的有穷非空集合，E是图G中边的有限集合。E（G）也可以为空集。若E（G）为空，则图G只有顶点而没有边。

其实，用句不是很严谨的话来说，图可以看成是没有任何限制的树（比如，可以有环状，可以有多种关系等等）。

❣️❣️顶点与边

图是由顶点集和边集组成。
- 图：一般使用G表示
- 顶点集：一般使用V表示，是一个有穷非空集合。由顶点组成，例如：u，v 等顶点。
- 边集：一般使用E表示，是一个有穷集合，可以是空集。由边组成，例如：e等边。
- 记作：G = (V, E)
- 零图：E可以是空集，此时图G只有顶点没有边，称为零图。
例如：

零图：

在图中，最基本的单元是顶点，相当于树中的节点，顶点之间的关联关系，被称为边。

还有一些图中，顶点之间的关联并不是完全对称的，举个例子比如说微博，你的粉丝列表里有我，但我的粉丝列表里未必有你，类似于这种单方面关注的，顶点之间的边就有了方向的区分，这种带有方向的图称为有向图。

❣️❣️无向图

无向边：顶点u和顶点v，在没有方向的情况下形成的边，简称为边。
- 记作：(u, v) = (v, u)，也就是 (u, v) 和 (v, u) 是等同的。
无向图（Undirected Graph）：全部由无向边构成的图。

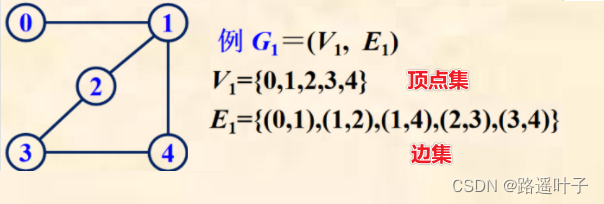
❣️❣️有向图

有向边：按照方向，从顶点u到顶点v形成的边，简称为弧。
- 记作：<u, v>、<v, u> ，也就是<u, v> 和 <v, u> 是不同的。
- 顶点u称为始点，或弧尾。
- 顶点v称为终点，或弧头。
有向图（Directed Graph）：全部由有向边构成的图。

💚❤️💙💚❤❤️💙💚❤️❤💙💚❤️💙❤💚❤️💙💚❤❤️💙💚❤️❤💙❤️💙💚❤❤️❤💙

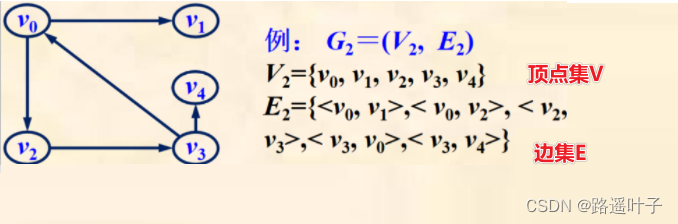
❣️❣️权和网

在一些图中，每一条边并不是完全等同的，使得边具有权重，涉及到权重的图，称为带权图 。

权重：与给定边之间的相关的成本。例如：航空公司航班图表，按城市之间的里程加权。

因此，综合有向无向、带权重不带权重，交叉来讲，图有带权重有向的、带权重无向的、不带权重的有向的、不带权重的无向的......

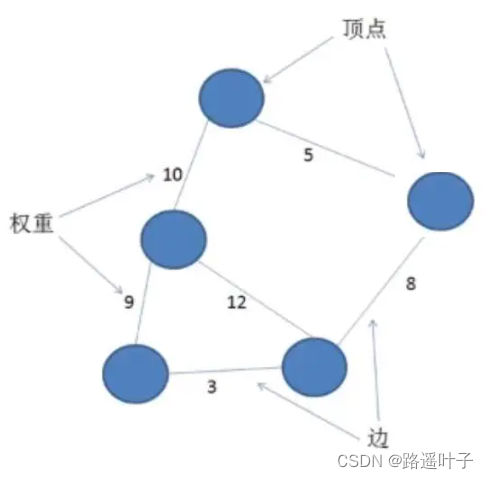
在某些实际场景中，图中的每条边（或弧）会赋予一个实数来表示一定的含义，这种与边（或弧）相匹配的实数被称为"权"，而带权的图通常称为网。如下图所示，就是一个网结构：

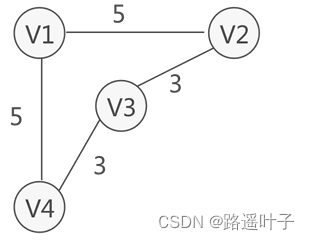
权（Weight）：在一个图中，每条边可以标上具有某种含义的数值，此数值称为该边上的权。

通常权是一个非负实数。

权可以表示从一个顶点到另一个顶点的距离、时间或代价等含义。

网（Network）：边上标识权的图。

❣️❣️完全图

在图论的数学领域，完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。完整的有向图又是一个有向图，其中每对不同的顶点通过一对唯一的边缘（每个方向一个）连接。n个端点的完全图有n个端点以及n(n − 1) / 2条边，以Kn表示。它是(k − 1)-正则图。所有完全图都是它本身的团。

无向完全图：每两个顶点之间都存在一条边。无向完全图是用n表示图中顶点数目的一种完全图，该图中每条边都是无方向的。在无向图中，如果任意两个顶点之间都存在边，则称该图为 无向完全图。

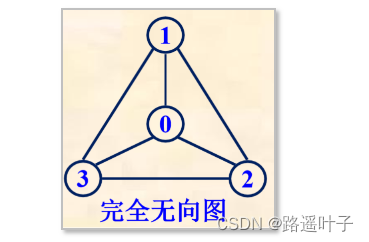
有向完全图：每两个顶点之间都存在着方向相反的两条边。有向完全图是指概述图中各边都有方向，且每两个顶点之间都有两条方向相反的边的连接图。

完全图有n个顶点，e条边，两者关系：

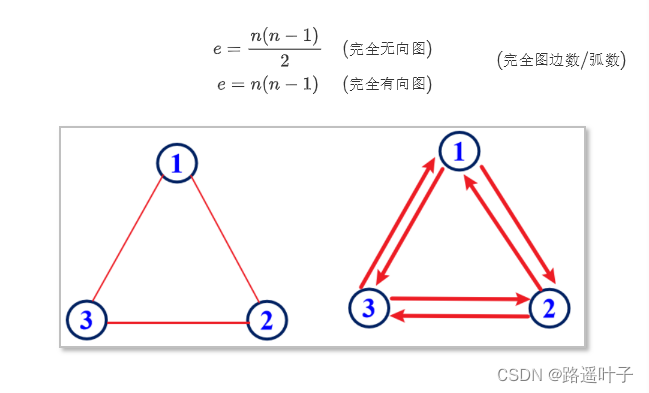
❣️❣️稠密图和稀疏图

稀疏图和稠密图：这两种图是相对存在的，即如果图中具有很少的边（或弧），此图就称为"稀疏图"；反之，则称此图为"稠密图"。

稀疏和稠密的判断条件是：e<nlogn，其中 e 表示图中边（或弧）的数量，n 表示图中顶点的数量。如果式子成立，则为稀疏图；反之为稠密图。

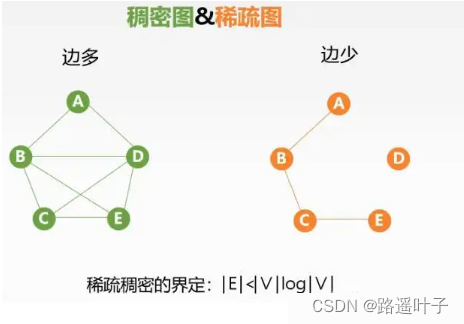
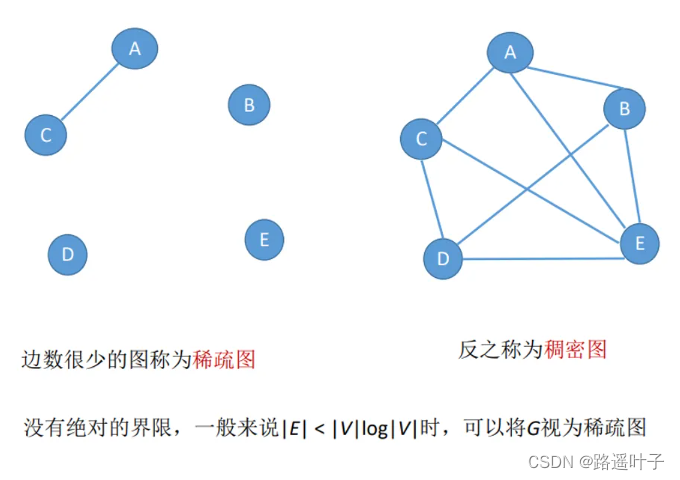
n为顶点数，e为边数，两图的相关计算如下：

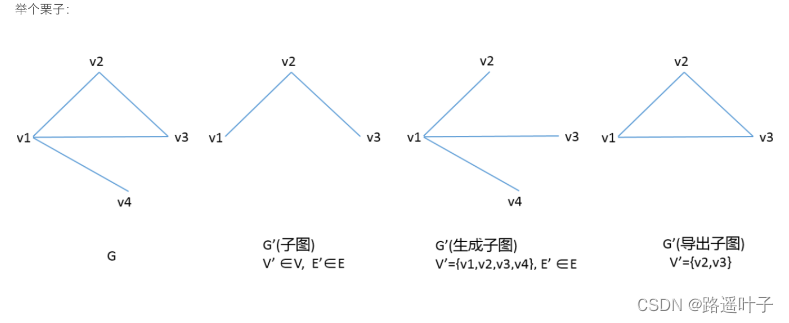
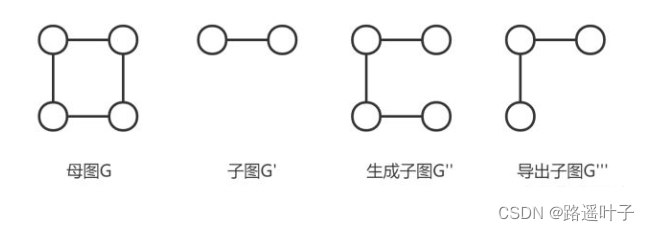
❣️❣️子图和生成子图

所有的顶点和边都属于图G的图称为G的子图。含有G的所有顶点的子图称为G的生成子图。

子图（Subgraph）

设有两个图 G=(V, E) 和 G'=(V', E')，若V‘是V的子集，即V’ ∈ V，并且E‘ 是 E的子集，即E’ ∈ E，则称 G‘ 为G的子图，记为 G’ ∈ G。

生成子图（Spanning Subgraph）

若G‘ 为G的子图，并且V’ = V，则称G‘ 为G的生成子图，即包含原图中所有顶点的子图。

导出⼦图(Induced Subgraph)
定义：导出⼦图G’，V’∈V，但对于V’中任⼀顶点，只要在原图G中有对应边，那么就要出现在E’中。

💚❤️💙💚❤❤️💙💚❤️❤💙💚❤️💙❤💚❤️💙💚❤❤️💙💚❤️❤💙❤️💙💚❤

❣️❣️邻接点

假若顶点v 和顶点w 之间存在一条边，则称顶点v 和w 互为邻接点。

在一个无向图中，若存在一条边(u,v)，则称顶点u与v互为邻接点。

边(u,v)是顶点u和v关联的边

顶点u和v是边(u,v)关联的顶点。

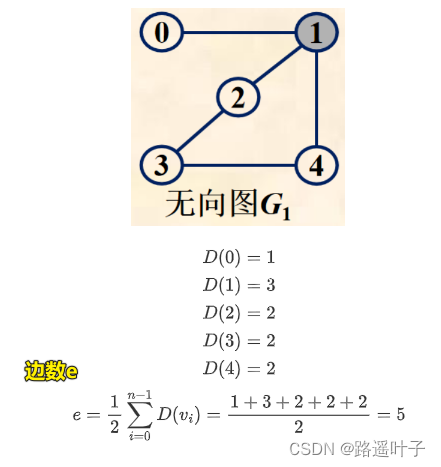
例如：以顶点1为端点的3条边是(0,1),(1,2),(1,4)，顶点1的3个邻接点分别为 0,2,4

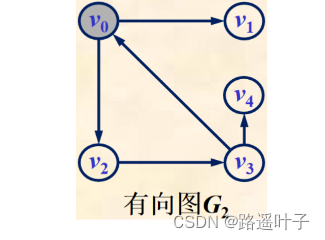
在一个有向图中，若存在一条弧<u,v>，则称顶点u邻接到v，顶点v邻接自u。

弧<u,v>和顶点u、v关联。

例如：顶点v0有2条出边<v0,v1>,<v0,v2>，1条入边<v3,v0>,顶点v0邻接到v1和v2,顶点v0邻接自v3

❣️❣️顶点的度

顶点的度（Degree）：图中与该顶点相关联边的数目。顶点v的度记为 D(v)。

若一个图有n个顶点和e条边，则该图所有顶点的度之和与边数满足如下关系：

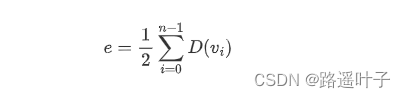
每条边关联两个顶点，对顶点的度贡献为2，所有全部顶点的度之和为所有边数的2倍。

无向图顶点的度：以该顶点为一个端点的边的数目，即该顶点的边的数目。

有向图顶点的度

入度(in degree)：顶点v的入边数目，称为该顶点的入度，记为 ID(v)。

以v为终点的弧的数目称为入度。

出度(out degree)：顶点v的出边数目，称为该顶点的出度，记为 OD(v)。

以v为起点的弧的数目称为出度。

顶点v的度：等于它的入度和出度之和。记作 D(v) = ID(v) + OD(v)

❣️❣️路径与回路

无论是无向图还是有向图，从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点），称为一条路径。如果路径中第一个顶点和最后一个顶点相同，则此路径称为"回路"（或"环"）。

并且，若路径中各顶点都不重复，此路径又被称为"简单路径"；同样，若回路中的顶点互不重复，此回路被称为"简单回路"（或简单环）。

拿下图来说，从 V1 存在一条路径还可以回到 V1，此 路径为 {V1,V3,V4,V1}，这是一个回路（环），而且还是一个简单回路（简单环）。

在有向图中，每条路径或回路都是有方向的。

路径(Path)：在一个图中，路径是从顶点u到顶点v所经过的顶点序列。

u=v0,v1,...vm = v
路径长度：该路径上边的数目。
回路：第一个顶点和最后一个顶点相同的路径，称为回路或环。
初等路径：序列中顶点不重复出现的路径。
初等回路：除了 第一个顶点和最后一个顶点 之外，其余顶点不重复出现的回路。
实例1：

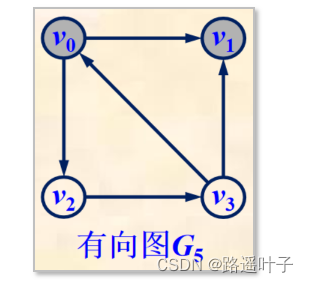
路径 (v0, v2, v3, v1) 是初等路径，其路径长度为3。

路径 (v0, v2, v3, v0, v1) 不是初等路径，其路径长度为4。

路径 (v0, v2, v3, v0) 是初等回路，其路径长度为3。

网中的路径长度：在网中，从始点到终点的路径上各边的权值之和，称为路径长度

实例2：从顶点A到顶点E的一条路径

(A, B, D, E) --> 路径长度：10 + 7 + 2 = 19

❣️❣️💚❤️💙💚❤❤️💙💚❤️❤💙💚❤️💙❤💚❤️💙💚❤❤️💙💚❤️❤💙❤️💙💚❤

如果文章对您有帮助，就拿起小手赶紧给博主点赞💚评论❤️收藏💙 一下吧！

想要了解更多吗？没时间解释了，快来点一点！

路遥叶子的博客_CSDN博客-数据结构,安利Java零基础,spring领域博主路遥叶子擅长数据结构,安利Java零基础,spring,等方面的知识,路遥叶子关注spring,spring boot,python,架构,java,mysql领域.https://blog.csdn.net/zsy3757486?spm=1011.2266.3001.5343https://blog.csdn.net/zsy3757486?spm=1011.2266.3001.5343