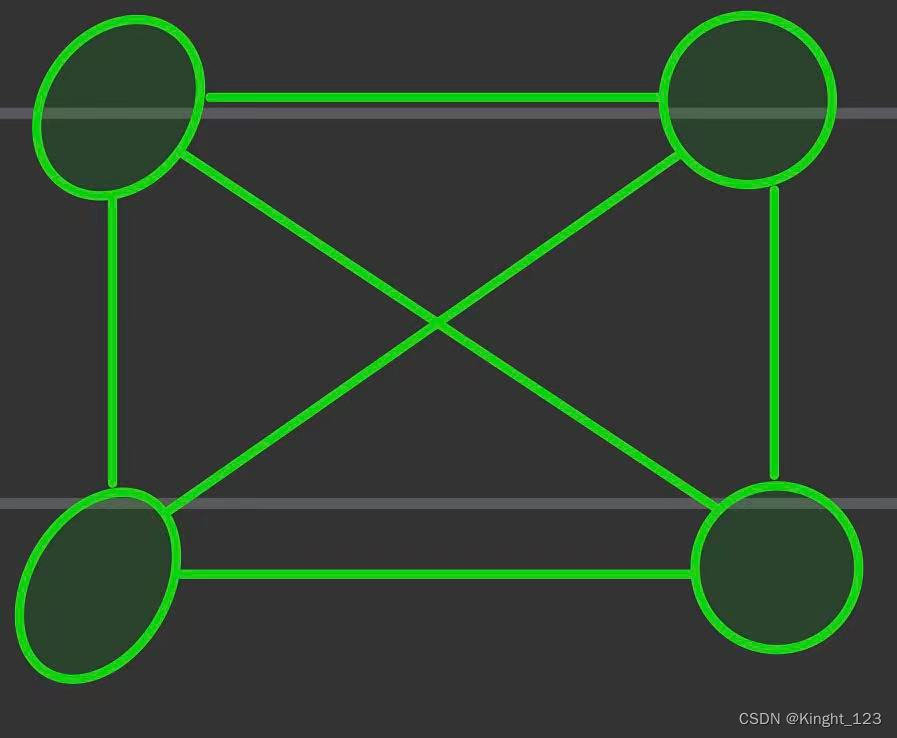
解题思想：

     对于图中所有节点，如果不相连，按照题意，必须在一个集合里；

     所以其实可以从第一个节点入手，找出与该点不相邻点的所有节点组成一个集合；

     判断剩余所有点，如果不和该集合中所有点都相连：按照题意，则无法构成完全多部图；

     如果和该集合中所有点都相连，则；

我们可以考虑，如果一个完全多部图去掉其中一个集合，则剩余的集合也是一个完全多部图；

所以，本题可以采用递归的思想：如果剩下的点也是完全多部图，则整个集合就是完全多部图。

     Base:

如果图中只有两个节点，则一定是完全多部图。（相连则划分为2个集合；不相连划分为一个集合）

代码实现（java）

import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;public class MainJD01 {public static void main(String[] args) {Scanner in = new Scanner(System.in);int t = in.nextInt();int n,m,x,y;int[][] adjArr;while(t-->0) {n = in.nextInt();m = in.nextInt();adjArr = new int[n][n];for (int i = 0; i < m; i++) {x = in.nextInt();y = in.nextInt();adjArr[x-1][y-1] = 1;adjArr[y-1][x-1] = 1;}List<Integer> list = new LinkedList<>();for (int i = 0; i < n; i++) {list.add(i);}if(judeg(list, adjArr)) System.out.println("Yes");elseSystem.out.println("No");}in.close();}/* * 1、* 	  1.1  节点数小于等于2必为完全多部图*    1.2  找出一个集合{节点互不相连}* 2、判断剩下的点时候都和这个集合里的点相连*    2.1 true:判断剩下节点是否是完全多部图*    2.2 false:结束*    */private static boolean judeg(List<Integer> list, int[][] adjArr) {if(list.size() <= 2)return true;List<Integer> listMinis = new LinkedList<>();listMinis.add(list.get(0));list.remove(0);for (int i = list.size()-1; i >= 0; i--) {if(adjArr[list.get(i)][listMinis.get(0)] == 0) {//和第一个顶点无连接listMinis.add(list.get(i));list.remove(i);}}for (int i = 0; i < listMinis.size(); i++) {for (int j = 0; j < list.size(); j++) {if(adjArr[list.get(j)][listMinis.get(i)] == 0)return false;}}return judeg(list, adjArr);}}

网上有个同学的想法是：

      1、如果两点不相连，则必在同一个集合里；
      2、同一个集合里的点因为需要与其他所有集合里的点都相连，所以关联的边数必须一致；
      3、遍历邻接表中所有点，如果不相连，则必须其关联的边数必须一致，否则则视为不能构成多部图

该想法是单项的必要条件而非充要条件。

反例：（环形图）