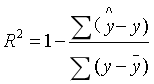相关文章
图论(2)完全图,顶点的度与度序列
目录
一、完全图 偶图(双图或二部图) (2)完全偶图 简单图的补图 自补图
二、顶点的度与图的度序列 顶点的度 图的度序列(注意与图序列的区别) 图序列 图的频序列及其性质
例题 一、完全图、偶图与补图
…
python散点图中如何添加拟合线并显示拟合方程与R方?
polyfit()函数可以使用最小二乘法将一些点拟合成一条曲线.
numpy.polyfit(x, y, deg, rcondNone, fullFalse, wNone, covFalse)
# x:要拟合点的横坐标
# y:要拟合点的纵坐标
# deg:自由度.例如:自由度为2,那么拟合出来的曲线就是二次函数,自由度是3,拟合出来的曲线就是3次函数…
一文搞定R语言拟合p值、R方...
R:ggplot2拟合,我推荐geom_smooth绘制拟合和ggpmisc添加统计信息。
几行代码就可以搞定了,对新手非常友好。
线性拟合
library(tidyverse)
library(readxl)
library(ggplot2)
library(ggpmisc)repeat1_rawgrassland <- read_excel("D:/OneDri…
R语言在逻辑回归中求R square R方
并非所有结果/因变量都可以使用线性回归进行合理建模。也许第二种最常见的回归模型是逻辑回归,它适用于二元结果数据。最近我们被客户要求撰写关于逻辑回归的研究报告,包括一些图形和统计输出。如何计算逻辑回归模型的R平方? 相关视频&…
Regression 中的 R方
最近在学习ML,一直看到这R方,明白什么意思,但是不知道怎么算出来的,今天看sklearn文档的时候偶然看到了,记录下 简而言之,他的值表示该系列数据是否适合该Regression 算法, 得分越靠近1越适合. 总结来说就是, 1 减去 ( 所有 ( ( 真实值 减去 预测值 ) 的平方 ) 和 除以 所有 (…
基于MATLAB的R方计算
R方计算原理
什么是R方
R-square是你以后很多数据模型都需要用到的统计量,计量模型什么的,还有回归系数显著性检验,F检验,德斌沃森统计量检验。利用数据拟合一个模型时,模型肯定存在误差,那么回归方程对观…
数据科学 | 如何解释线性回归的R方
R方,即R-Squared,常用来衡量线性回归的拟合度。相关性“r"衡量两个变量间的相关性,相关性接近1表示变量间具有很强的正相关性,接近-1表示变量间具有很强的负相关性,接近0表示变量间没有太多的关系。R方与相关性”…
什么是R方?这6张图会让你终身难忘~
什么是R2 ? 在回归模型中,因变量(y)总的方差(信息)可以被称作总平方和(Total sum of squares,TSS),它由两部分组成[1]: 1. 模型可以解释的那部分信…
贝叶斯相关公式(Bayes)
这里只是记录一下,非常推荐马同学高等数学,文末有原文.点击这里看里面的例一应该是理解贝叶斯公式最好的例子 ,如果你稍微有一些基础,我觉得文末第二个链接中的例一更加适合你
代数推导
1. 贝叶斯公式
是根据条件概率推导的 P(A|B)P(AB)P(B)P(B|A)…
贝叶斯模型及其应用总结
本文参考整理众多资料而成。
http://blog.csdn.net/huaxi1902/article/details/24140061 http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/
http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html
http://www.ruanyifeng.com/blog/2011/08…
贝叶斯预测模型 (数学原理与推导)
1. 方差的两种计算方法 对于方差计算的一个重要结论: 2. 联合概率分布-条件概率分布
当然,利用联合概率分布也很容易推出边缘概率分布;只需要对其他变量进行全积分即可! 条件概率分布直观想象还是有难度的,很多时候我…
朴素贝叶斯算法 — 超详细公式讲解+代码实例
本文收录于Github仓库,欢迎前来 star 呀~ https://github.com/Veal98/cs-wiki在线阅读地址/更好的阅读体验请移步:cswiki.top
👔 朴素贝叶斯算法 Naive Bayes 💡 思维导图 1. 朴素贝叶斯法概述
朴素贝叶斯法是基于贝叶斯定理与…
ubuntu DBUS 收集
ubuntu DBUS 收集
libdbus-1.so.3.19.11 是dbus-1.12.16.tar.gz 包编译出来的
参考文档:
https://www.freedesktop.org/wiki/Software/dbus/ https://www.freedesktop.org/wiki/IntroductionToDBus/ https://dbus.freedesktop.org/doc/dbus-tutorial.html https://docs.gtk.…
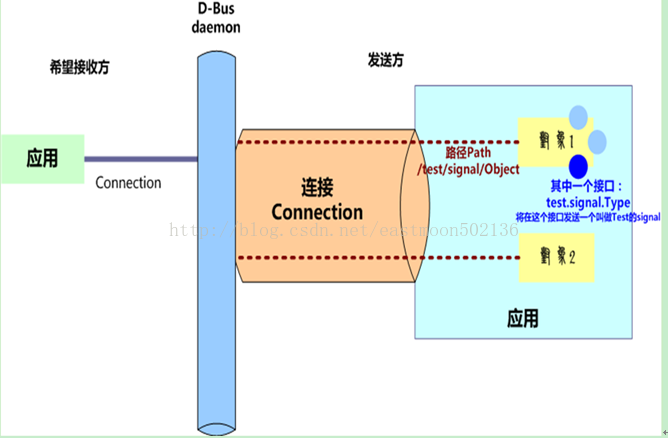
Linux DBUS服务器端程序
DBus 服务器端接收方式
DBus 服务器端用来接收signal和method调用。从收集的资料中发现,主要有三种接收方式。
一,采用while循环,监听dbus_connection_read_write()函数。有消息到来时在循环内部进行处理。优点是结构简单,处理方…
Linux -dbus总线
下载编译dbus
下载https://dbus.freedesktop.org/releases/dbus/
dbussrc1.14.0-Linux文档类资源-CSDN下载
dbus-1.14.0.tar.xz
xz -d dbus-1.14.0.tar.xz
tar xvf dbus-1.14.0.tar2.配置编译
./configure --prefix/data/opensrc/dbus #--prefix/data/opensrc/dbus 指定输…