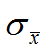前面我们讨论的关联规则都是用支持度和自信度来评价的，如果一个规则的自信度高，我们就说它是一条强规则，但是自信度和支持度有时候并不能度量规则的实际意义和业务关注的兴趣点。
一个误导我们的强规则
看这样一个例子，我们分析一个购物篮数据中购买游戏光碟和购买影片光碟之间的关联关系。交易数据集共有10,000条记录，其中购买6000条包含游戏光碟，7500条包含影片光碟，4000条既包含游戏光碟又包含影片光碟。数据集如下表所示：
| 买游戏 | 不买游戏 | 行总计 | |
| 买影片 | 4000 | 3500 | 7500 |
| 不买影片 | 2000 | 500 | 2500 |
| 列总计 | 6000 | 4000 | 10000 |
假设我们设置得最小支持度为30%，最小自信度为60%。从上面的表中，可以得到：support(买游戏光碟—>买影片光碟)=4000/10000=40%，confidence(买游戏光碟—>买影片光碟)=4000/7500*100%=66%（写错了，应该是4000/6000）。这条规则的支持度和自信度都满足要求，因此我们很兴奋，我们找到了一条强规则，于是我们建议超市把影片光碟和游戏光碟放在一起，可以提高销量。
可是我们想想，一个喜欢的玩游戏的人会有时间看影片么，这个规则是不是有问题，事实上这条规则误导了我们。在整个数据集中买影片光碟的概率p(买影片)=7500/10000=75%，而买游戏的人也买影片的概率只有66%，66%<75%恰恰说明了买游戏光碟抑制了影片光碟的购买，也就是说买了游戏光碟的人更倾向于不买影片光碟，这才是符合现实的。
从上面的例子我们看到，支持度和自信度并不能过成功滤掉那些我们不感兴趣的规则，因此我们需要一些新的评价标准，下面介绍六中评价标准：相关性系数，卡方指数，全自信度、最大自信度、Kulc、cosine距离。
相关性系数lift
从上面游戏和影片的例子中，我们可以看到游戏和影片不是正相关的，因此用相关性度量关联规则可以过滤这样的规则，对于规则A—>B或者B—>A，lift(A,B)=P(A交B)/(P(A)*P(B))，如果lift(A,B)>1表示A、B呈正相关，lift(A,B)<1表示A、B呈负相关，lift(A,B)=1表示A、B不相关（独立）。实际运用中，正相关和负相关都是我们需要关注的，而独立往往是我们不需要的，两个商品都没有相互影响也就是不是强规则，lift(A,B)等于1的情形也很少，一般只要接近于1我们就认为是独立了。
注意相关系数只能确定相关性，相关不是因果，所以A—>B或者B—>A两个规则的相关系数是一样的，另外lift(A,B)=P(A交B)/(P(A)*P(B))=P(A)*P(B|A)/(P(A)*P(B))=P(B|A)/P(B)=confidence(A—>B)/support(B)=confidence(B—>A)/support(A)。
卡方系数![clip_image002[4]](http://images0.cnblogs.com/blog/431880/201308/13150754-7a5a0718a44b4f5aa5fe90b0ebeec715.gif "clip_image002[4]"){kind=small}
卡方分布是数理统计中的一个重要分布，利用卡方系数我们可以确定两个变量是否相关。卡方系数的定义:
![clip_image002[8]](http://images0.cnblogs.com/blog/431880/201308/13150754-45ea3dff49e742fe892da9b037286712.gif "clip_image002[8]"){kind=small}
公式中的observed表示数据的实际值,expected表示期望值,不理解没关系,我们看一个例子就明白了。
| 买游戏 | 不买游戏 | 行总计 | |
| 买影片 | 4000(4500) | 3500(3000) | 7500 |
| 不买影片 | 2000(1500) | 500(1000) | 2500 |
| 列总计 | 6000 | 4000 | 10000 |
上面表格的括号中表示的是期望值，(买影片，买游戏)的期望值E=6000*(7500/10000)=4500，总体记录中有75%的人买影片，而买游戏的有6000人，于是我们期望这6000人中有75%(即4500)的人买影片。其他三个值可以类似计算得到。现在我们计算一下，买游戏与买影片的卡方系数：
卡方系数X=(4000-4500)^2/4500+(3500-3000)^2/3000+(2000-1500)^2/1500+(500-1000)^2/1000=555.6。
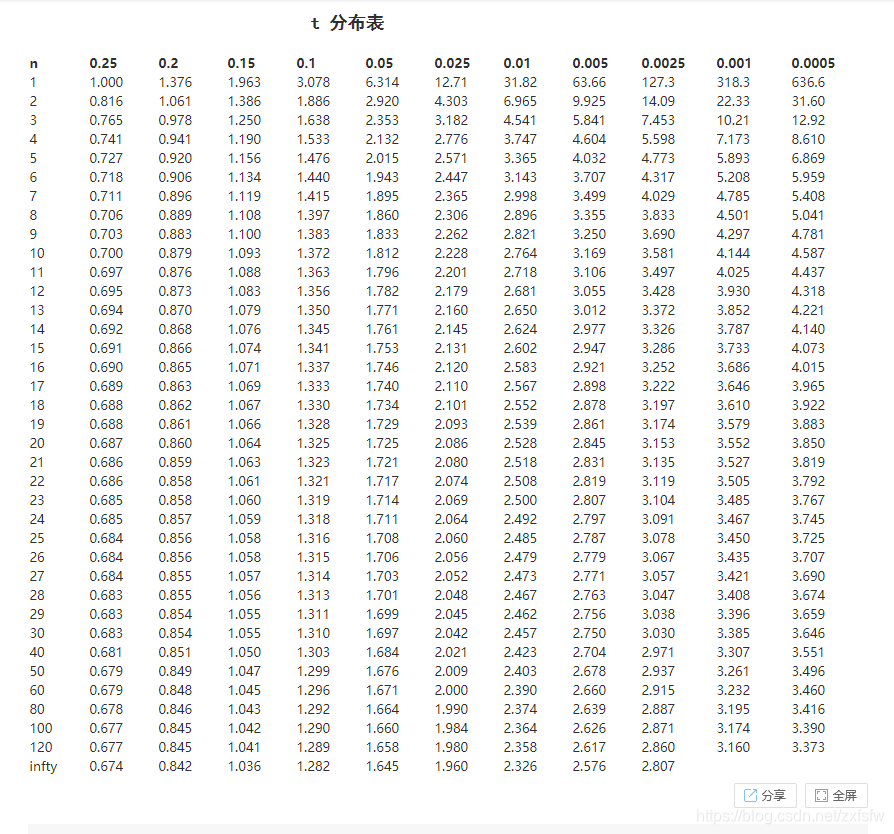
卡方系数需要查表才能确定值的意义，基于置信水平和自由度(r-1)*(c-1)=(行数-1)*(列数-1)=1，查表得到自信度为(1-0.001)的值为6.63，555.6大于6.63，因此拒绝A、B独立的假设，即认为A、B是相关的，而expected(买影片，买游戏)=4500>4000,因此认为A、B呈负相关。这里需要一定的概率统计知识。如果觉得不好理解，可以用其他的评价标准。
全自信度
全自信度all_confidence的定义如下：all_confidence(A,B)=P(A交B)/max{P(A),P(B)}
=min{P(B|A),P(A|B)}
=min{confidence(A—>B),confidence(B—>A)}
对于前面的例子，all_confidence(买游戏，买影片)=min{confidence(买游戏—>买影片),confidence(买影片—>买游戏)}=min{66%,53.3%}=53.3%。可以看出全自信度不失为一个好的衡量标准。
最大自信度
最大自信度则与全自信度相反，求的不是最小的支持度而是最大的支持度，max_confidence(A,B)=max{confidence(A—>B),confidence(B—>A)}，不过感觉最大自信度不太实用。
Kulc
Kulc系数就是对两个自信度做一个平均处理：kulc(A,B)=(confidence(A—>B)+confidence(B—>A))/2。，kulc系数是一个很好的度量标准，稍后的对比我们会看到。
cosine(A,B)
cosine(A,B)=P(A交B)/sqrt(P(A)*P(B))=sqrt(P(A|B)*P(B|A))=sqrt(confidence(A—>B)*confidence(B—>A))
七个评价准则的比较
这里有这么多的评价标准，究竟哪些好，哪些能够准确反应事实，我们来看一组对比。
| milk | milk | 行总计 | |
| coffee | MC | MC | C |
| coffee | MC | MC | C |
| 列总计 | M | M | total |
上表中，M表示购买了牛奶、C表示购买了咖啡,M表示不购买牛奶，C表示不购买咖啡，下面来看6个不同的数据集，各个度量标准的值
| 数据 | MC | MC | MC | MC | total | C->M自信度 | M->C自信度 | 卡方 | lift | all_conf | max_conf | Kulc | cosine |
| D1 | 10000 | 1000 | 1000 | 100000 | 112000 | 0.91 | 0.91 | 90557 | 9.26 | 0.91 | 0.91 | 0.91 | 0.91 |
| D2 | 10000 | 1000 | 1000 | 100 | 12100 | 0.91 | 0.91 | 0 | 1.00 | 0.91 | 0.91 | 0.91 | 0.91 |
| D3 | 100 | 1000 | 1000 | 100000 | 102100 | 0.09 | 0.09 | 670 | 8.44 | 0.09 | 0.09 | 0.09 | 0.09 |
| D4 | 1000 | 1000 | 1000 | 100000 | 103000 | 0.50 | 0.50 | 24740 | 25.75 | 0.50 | 0.50 | 0.50 | 0.50 |
| D5 | 1000 | 100 | 10000 | 100000 | 111100 | 0.91 | 0.09 | 8173 | 9.18 | 0.09 | 0.91 | 0.50 | 0.29 |
| D6 | 1000 | 10 | 100000 | 100000 | 201010 | 0.99 | 0.01 | 965 | 1.97 | 0.01 | 0.99 | 0.50 | 0.10 |
我们先来看前面四个数据集D1-D4，从后面四列可以看出，D1,D2中milk与coffee是正相关的，而D3是负相关，D4中是不相关的，大家可能觉得，D2的lift约等于1应该是不相关的，事实上对比D1你会发现，lift受MC的影响很大，而实际上我们买牛奶和咖啡的相关性不应该取决于不买牛奶和咖啡的交易记录，这正是lift和卡方的劣势，容易受到数据记录大小的影响。而全自信度、最大自信度、Kulc、cosine与MC无关，它们不受数据记录大小影响。卡方和lift还把D3判别为正相关，而实际上他们应该是负相关，M=100+1000=1100，如果这1100中有超过550的购买coffee那么就认为是正相关，而我们看到MC=100<550，可以认为是负相关的。
上面我们分析了全自信度、最大自信度、Kulc、cosine与空值无关，但这几个中哪一个更好呢？我们看后面四个数据集D4-D6,all_conf与cosine得出相同的结果，即D4中milk与coffee是独立的，D5、D6是负相关的，D5中support（C-->M）=0.91而support（M-->C）=0.09，这样的关系，简单的认为是负相关或者正相关都不妥，Kulc做平均处理倒很好，平滑后认为它们是无关的，我们再引入一个不平衡因子IR(imbalance ratio):
IR(A,B)=|sup(a)-sup(B)|/(sup(A)-sup(B)-sup(A交B))（注：应为(sup(A)+sup(B)-sup(A交B)）
D4总IR(C,M)=0，非常平衡，D5中IR(C,M)=0.89,不平衡，而D6中IR(C,M)=0.99极度不平衡，我们应该看到Kulc值虽然相同但是平衡度不一样，在实际中应该意识到不平衡的可能，根据业务作出判断，因此这里我们认为Kulc结合不平衡因子的是较好的评价方法。
另外weka中还使用 Conviction和Leverage。Conviction(A,B) = P(A)P(B)/P(AB)， Leverage(A,B) = P(A交B)-P(A)P(B)，Leverage是不受空值影响，而Conviction是受空值影响的。
总结
本文介绍了9个关联规则评价的准则，其中全自信度、最大自信度、Kulc、cosine，Leverage是不受空值影响的，这在处理大数据集是优势更加明显，因为大数据中想MC这样的空记录更多，根据分析我们推荐使用kulc准则和不平衡因子结合的方法。
参考文献
[1]：HanJiaWei. Data Mining: concept and techniques.
