树的同构
- 树的同构
- 输入格式:
- 输出格式:
- 输入样例1(对应图1):
- 输出样例1:
- 输入样例2(对应图2):
- 输出样例2:
- 题意理解
- 输入两棵二叉树的信息,判断是否同构(对应图1)
- 求解思路
- 二叉树表示
- 程序框架搭建
- 建二叉树
- 同构判别(如何判别二叉树同构)
- 树的同构源码
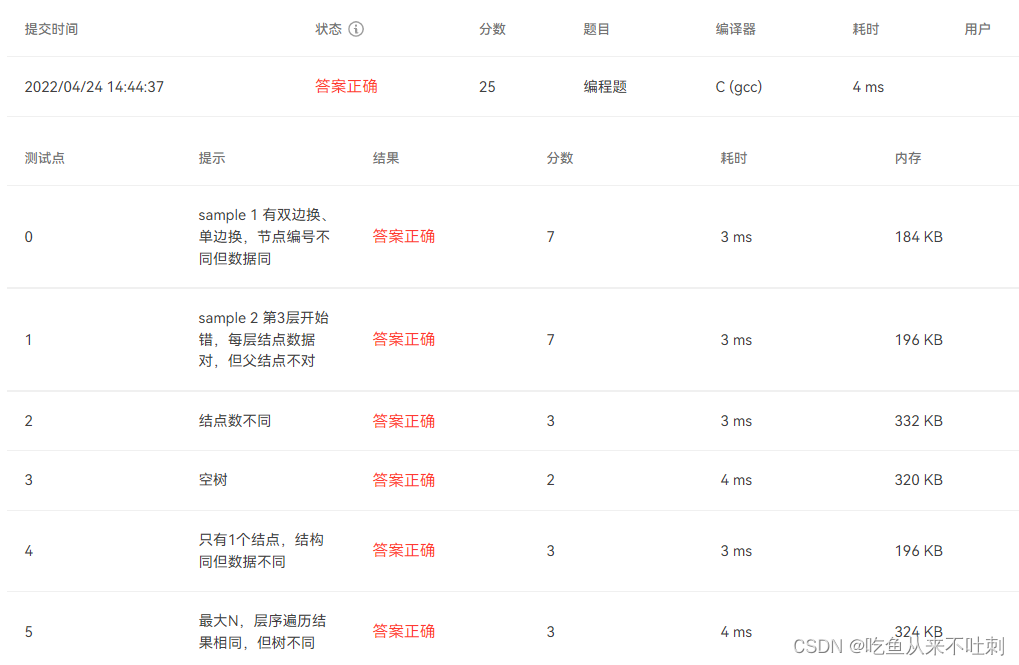
- 运行截图
树的同构
03-树1 树的同构 (25 分)
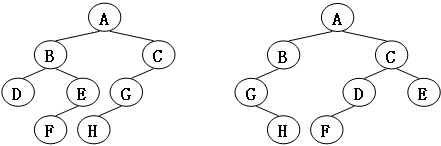
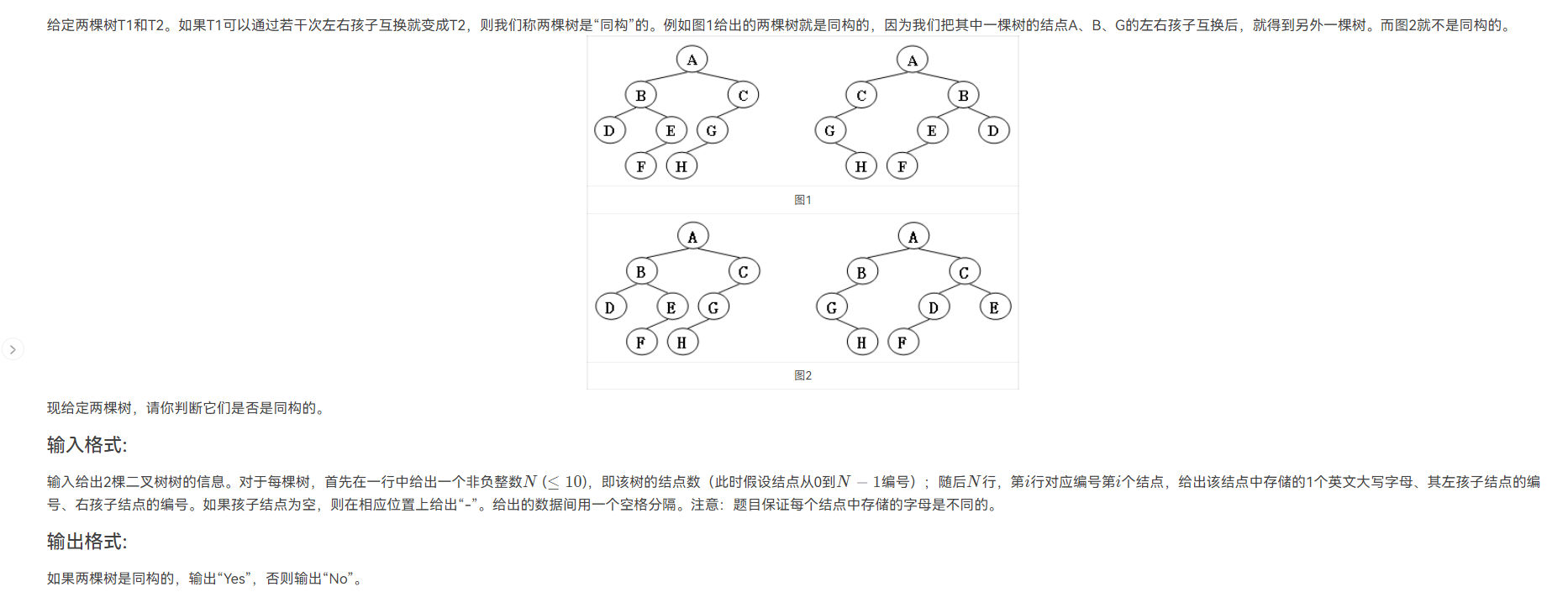
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
题意理解
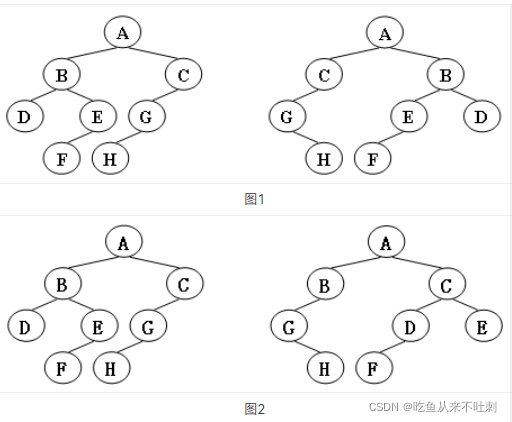
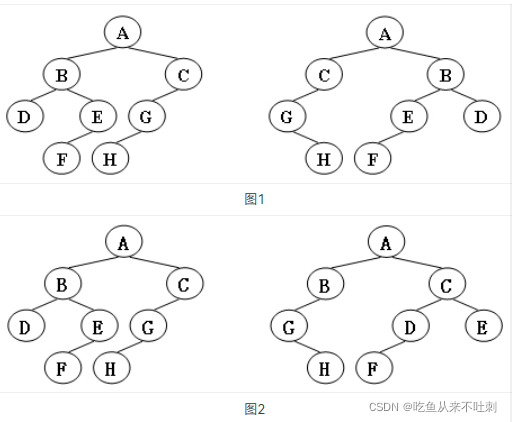
- 对于图1,是同构的
- 对于图2:C在图二的左边图形里只有一个儿子G,在图二的右边图形里有两个儿子D、E,所以就不是同构
- 树的同构,顾名思义两个树是否有一样的结构,每一个孩子结点的孩子的数量和值都要相同,但是它所在的位置可以左右交换(不是说两个父亲结点(B、C)的孩子互相交换,而是说父亲结点的下一层孩子的左右可以交换,如D与E可以互换)
输入两棵二叉树的信息,判断是否同构(对应图1)
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
- 第一个数是个整数,告诉整个二叉树有几个结点,该题有8个
- 每个结点信息有三个数据,第一个代表了这个结点本身的信息,字符来代表每个结点,后面是两个整数,代表当前这个结点的左儿子是谁,右儿子是谁
- 比方说A,左儿子是B,右儿子是C,B的编号是1,C的编号是2
- D左右儿子都没有,就用两个杠来分别说明左右儿子都是空的
- 第二棵树也是一样的道理,这样的输入方法里,不要求根节点作为第一个数据来输入
求解思路
二叉树表示
-
链表:left和right两个指针
-
一般数组(看成完全二叉树,按照完全二叉树的方法来表示)

-
结构数组(静态链表)

- 物理上存储是数组,把所需要的信息存储在数组里面,但左右儿子用类似链表的方法来表示,有一个数据来指示左儿子在哪,右儿子在哪,思想上是链表
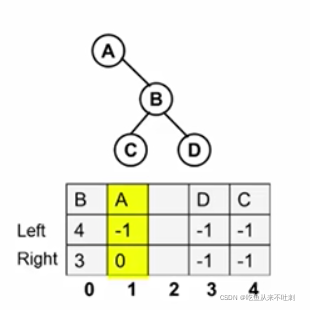
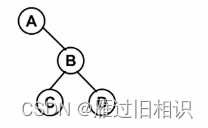
- ABCD表示结点本身的信息,用来标识结点,left和right不是指向左儿子右儿子的指针,而是指向左儿子和右儿子位置的下标,是个整数,数组正常的下标是从0开始的,所以用-1表示他指向的是一个空的结点,C语言中NULL为0,这里重新定义一个Null=-1
- 此时,ABCD的表示不是唯一的,顺序可以变换
判别根节点:四个数据分别在0,1,3,4
其中,0,3,4在结构数组里的left、right中出现了,则1所对应的结点为根节点
程序框架搭建
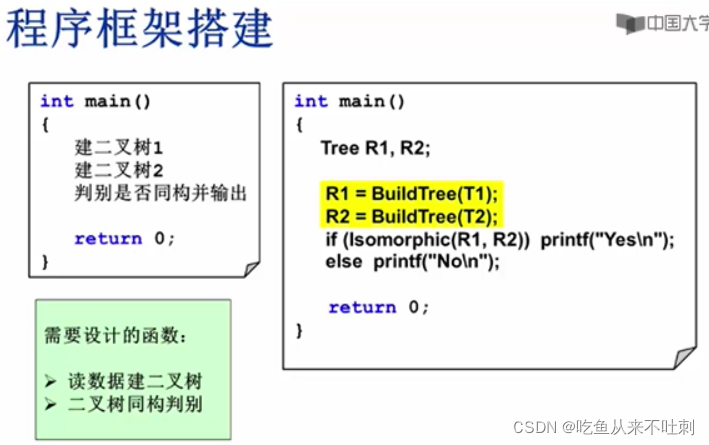
通过BuildTree建立两棵二叉树T1和T2,在调用Isomorphic来判别这两棵二叉树是不是同构
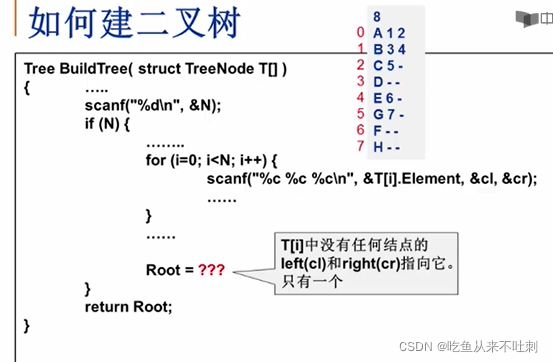
建二叉树

- 输入N,N不空的话,执行循环。为了处理方便,三个读进来的时候,都处理成字符的方式读进来,再把left和right由字符转换成整数,最后返回树根
- 把这个结构数组从头到尾扫描一遍,看看有没有哪个结点不存在其他节点指向它,没人指向它,就是根节点了
就是把T[i]这个数组遍历一遍看看有没有谁指向它
用一个数组check,它对应的是我们的N个节点,就是结构数组的那N个节点,check的值一开始都等于0,就是每个节点所对应的check一开始都等于0,然后就是在信息读的过程中就Element里的left和right读进来之后,同时对它的left和right进行处理,如果一个结点有一个left指向了某个位置,就把那个位置的check设为1,如果读进来这个right,指向另外一个结点,那么就把right指向那个位置checek设为1,所以在读每行信息的同时,就把对应的,他指向的,那些结点的check都设为1,一开始都是0,如果有人指向它,它就被设为1
所以整个循环过后,没有被设为1,仍为0的结点就是根节点了
同构判别(如何判别二叉树同构)

- 如果两个数都是空的,也就是R1和R2的值都是-1,两个空树是同构的,return 1
- 一个空,一个不空,那就不同构,return 0
- 树根值不一样,一个是A,一个是B,肯定不同构,return 0
- 这两棵树的左子树都是空的,那就看右边同构不同构,递归调用右子树的判别。
- 左边不是同时空的情况

- 左边如果同时不空,就看左边的Element是不是一样的,是一样的,就看左边相等不相等,右边相等不相等
- 若Element值是不一样的,调用左和右的判别
- 两棵树,一棵左边空,一棵左边不空,也是左边和右边的判别
树的同构源码
#include<stdio.h>#define MaxTree 10
#define ElementType char
#define Tree int
#define Null -1 //将Null定义为-1而不能是0,因为数组下标为0的地方仍保存有节点
typedef struct TreeNode TreeNode;
struct TreeNode {ElementType Element;Tree Left;Tree Right;
}T1[MaxTree],T2[MaxTree];Tree BuildTree(TreeNode T[]) {int i, N;int check[MaxTree]; //check数组用于寻找树的根节点int Root;char cl, cr;scanf("%d\n",&N);if (N) {for (i = 0; i < N; i++) check[i] = 0; /*每个节点所对应的check一开始都等于0*/for (i = 0; i < N; i++) {scanf("%c %c %c\n", &T[i].Element, &cl, &cr);if (cl != '-') {T[i].Left = cl - '0'; //字符转化为整数check[T[i].Left] = 1;//检查数组中的相应位置赋为1}else T[i].Left = Null; //不存在就设置为-1/*对cr的对应处理*/if (cr != '-') //右子树也一样{T[i].Right = cr - '0';check[T[i].Right] = 1;}else T[i].Right = Null;}}else return Null;/*空树*/for (i = 0; i < N; i++)if (!check[i]) break; /*//如果为0 则退出,此时i为根节点*/Root = i;return Root;
}int Isomorphic(Tree R1, Tree R2) {/*如果两个数都是空的,也就是R1和R2的值都是-1,两个空树是同构的,return 1*/if ((R1 == Null) && (R2 == Null)) return 1;/*一个空,一个不空,那就不同构,return 0*/if (((R1 == Null) && (R2 != Null)) || ((R1 != Null) && (R2 == Null)))return 0;/*树根值不一样,一个是A,一个是B,肯定不同构,return 0*/if (T1[R1].Element != T2[R2].Element) return 0;/*这两棵树的左子树都是空的,那就看右边同构不同构,递归调用右子树的判别。*/if ((T1[R1].Left == Null) && (T2[R2].Left == Null))return Isomorphic(T1[R1].Right, T2[R2].Right);/* 如果两棵树左儿子都不为空并且数据还是一样的,即左子树的根结点相同 ,则递归调用,左子树与左子树判别,右子树与右子树判别*/if( ((T1[R1].Left!=Null)&&(T2[R2].Left!=Null))&&((T1[T1[R1].Left].Element)== (T2[T2[R2].Left].Element)) )return(Isomorphic(T1[R1].Left, T2[R2].Left) &&Isomorphic(T1[R1].Right, T2[R2].Right));/* 如果两棵树左儿子(一个空一个不空或者都不空)并且数据不一样,即左子树的根结点不同,那么判断第一棵树的左(右)儿子是否跟第二棵树的右(左)儿子同构,即则左子树与右子树判别,右子树与左子树判别 */elsereturn (Isomorphic(T1[R1].Left, T2[R2].Right) &&Isomorphic(T1[R1].Right, T2[R2].Left));
}int main() {Tree R1, R2; //首先建立两棵树,R1,R2为树的根节点R1 = BuildTree(T1);R2 = BuildTree(T2);if (Isomorphic(R1, R2)) //Isomorphic函数判断是否同构printf("Yes\n");else printf("No\n");return 0;
}运行截图
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
^Z
Yes