文章目录
- 数据探索
- 数据探索的角度
- 1 数据质量分析
- 缺失值分析
- 异常值分析
- 一致性分析
- 2 数据特征分析
- 分布分析
- 对比分析
- 统计量分析
- 周期性分析
- 贡献度分析
- 相关性分析
数据探索
根据观测、调查收集到初步的样本数据集后,接下来要考虑的问题是:
- 样本数据集的数量和质量是否满足模型构建的要求?
- 有没有出现从未设想过的数据状态?
- 其中有没有明显的规律和趋势?
- 各因素之间有什么样的关联性?
数据探索的角度
通过检验数据集的数据质量、绘制图表、计算某些特征量等手段,对样本数据集的结构和规律进行分析的过程就是数据探索。通常从以下两个角度入手:
- 数据质量分析
- 数据特征分析
1 数据质量分析
数据质量分析的主要任务是:检查原始数据中是否存在脏数据。
脏数据一般是指不符合要求以及不能直接进行相应分析的数据,主要包括:缺失值、异常值、不一致的数据、重复的数据以及含有特殊符号( #、¥、* )的数据。
缺失值分析
缺失值产生的原因:
-
有些信息暂时无法获取,或者获取信息的代价太大。
-
有些信息是被遗漏的。
-
人为因素:
-
输入是认为不重要
-
忘记填写
-
对数据错误理解
-
-
非人为因素:
-
数据采集设备故障
-
存储介质故障
-
传输媒体故障
-
-
-
属性值不存在:缺失值并不意味着数据有错误。有一些对象的某些属性值是不存在的。例如:未婚者的配偶姓名、一个儿童的固定收入。
缺失值的影响:
- 数据挖掘建模将丢失大量的有用信息。
- 数据挖掘建模所表现出的不确定性更加显著,模型中蕴含的规律更难把握。
- 包含控制的数据会使建模过程陷入混乱,导致不可靠的输出。
缺失值的分析:
- 使用简单的统计分析,可以得到含有缺失值的属性的个数以及每个属性的未缺失数、缺失数与缺失率等。
- 对于缺失值的处理
- 删除存在缺失值的记录
- 对可能值进行插补
- 不处理
异常值分析
异常值分析是检验数据是否有录入错误,是否含有不符合常理的数据。
异常值指样本中的个别值,其数值明显偏离其他的观测值。异常值也成为离群点,异常值分析也成为离群点分析。
常见的异常值分析方法:
💠简单统计量分析
最常使用最大值和最小值,来判断某个变量是否超出了合理的范围。
• 例如,客户年龄的最大值为199岁,则判断年龄这个变量的取值存在异常值。
💠3 δ原则
• 如果数据服从正态分布,在3 δ原则下,异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。
P(|x- μ |> 3 δ) ≤0.003
• 如果不服从正态分布,也可以永远离平均值的标准差倍数来描述。
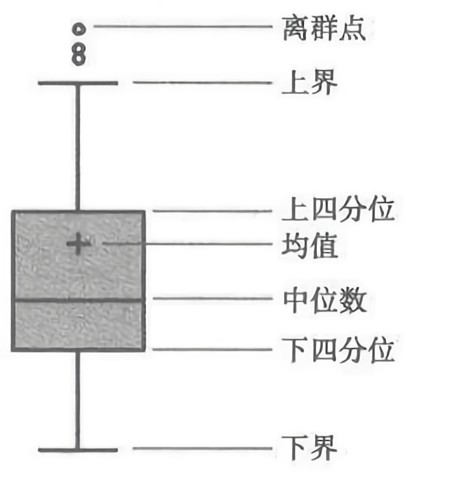
💠箱型图分析
• Qu(上四分位数):全部观察之中有四分之一的数据取值比它大。
• Ql(下四分位数):全部观察之中有四分之一的数据取值比它小。
• IQR(四分位间距,=Qu-Ql):包含了全部观察值的一半。
• 上界:非离群点中的最大值。
• 下界:非离群点中的最小值。
• 离群点(异常点):通常定义为Ql-1.5IQR或 者Qu+1.5IQR的值。
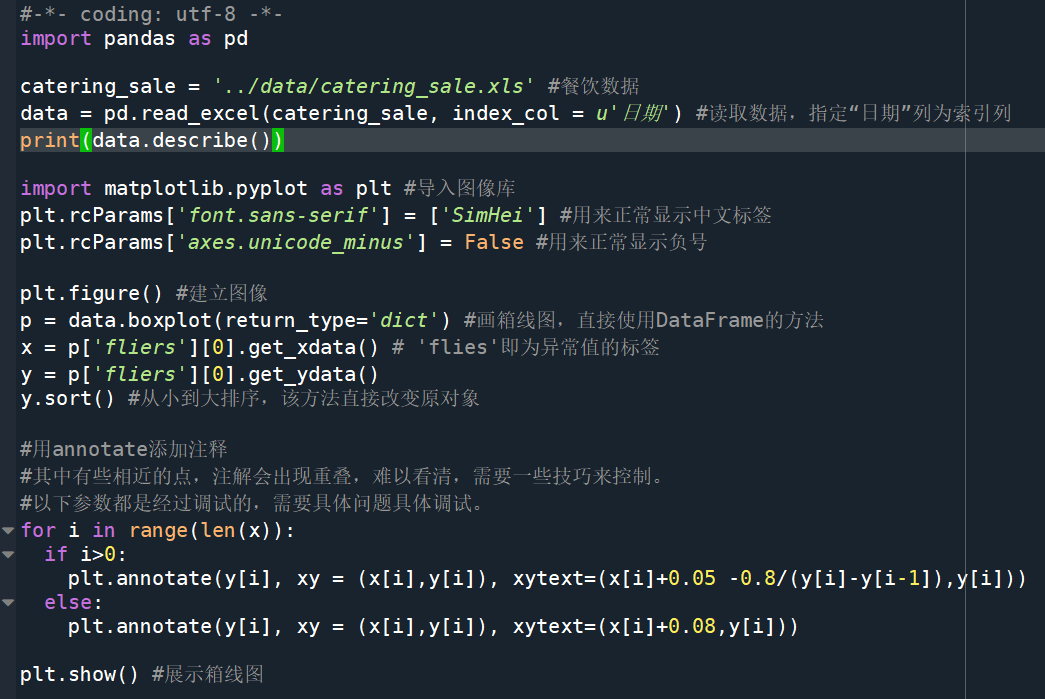
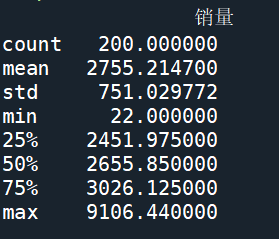
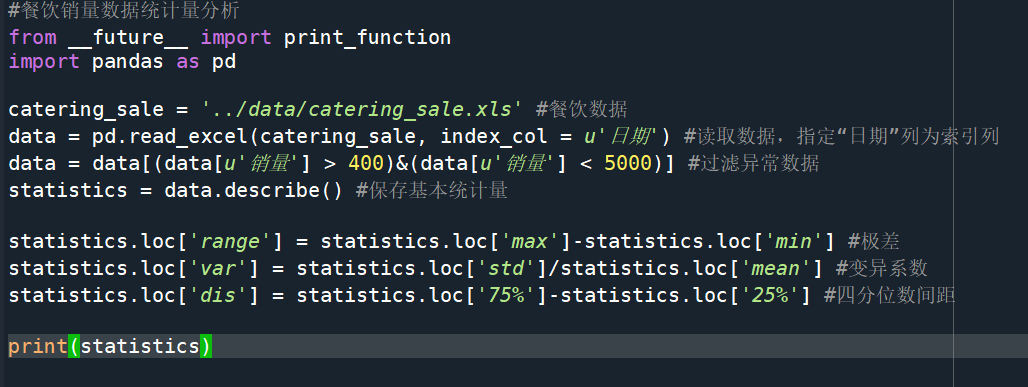
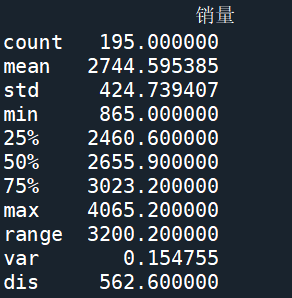
例:T餐饮的异常值分析

一致性分析
- 数据不一致性是指数据的矛盾性、不相容性。
- 不一致数据主要发生在数据集成过程中,可能是由于被挖掘数据来自于不同的数据源、对于重复存放的数据未能进行一致性更新造成的。
- 例如:两张表中都存放了用户的电话号码,但在用户电话号码发生改变时,只更新了其中一张表中的数据,那么,这两张表中就有了不一致的数据。
2 数据特征分析
- 分布分析
- 对比分析
- 统计量分析
- 周期性分析
- 贡献度分析
- 相关性分析
分布分析
分布分析能解释数据的分布特征和分布类型。
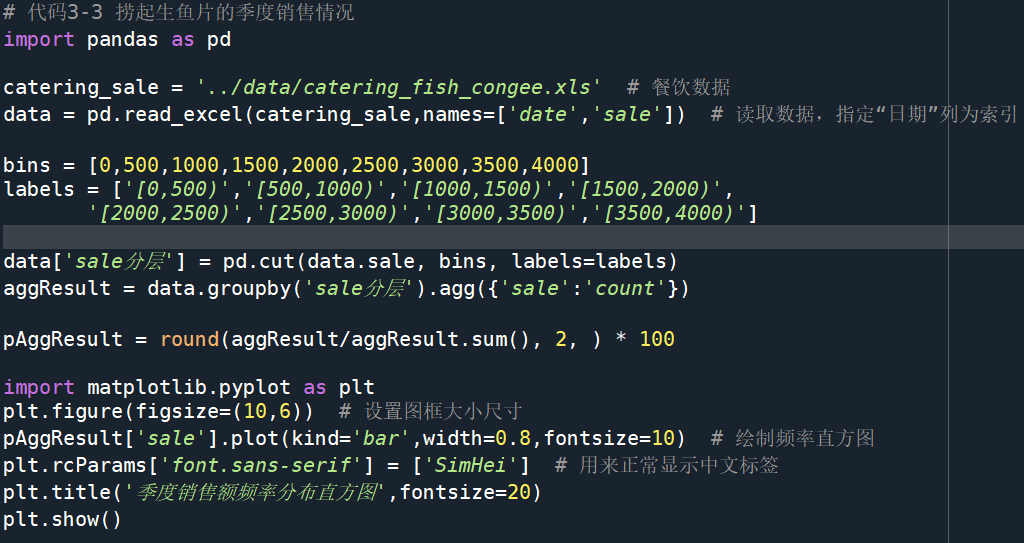
- 对于定量数据,要想了解其分布形式是对称的还是非对称的、发现某些特大或特效的可疑值,可作出频率分布表、绘制频率分布直方图、绘制茎叶图进行直观分析。
- 对于定性数据,可疑用饼图和条形图直观的显示其分布。
定量数据(‘捞起生鱼片’的销售布情况)
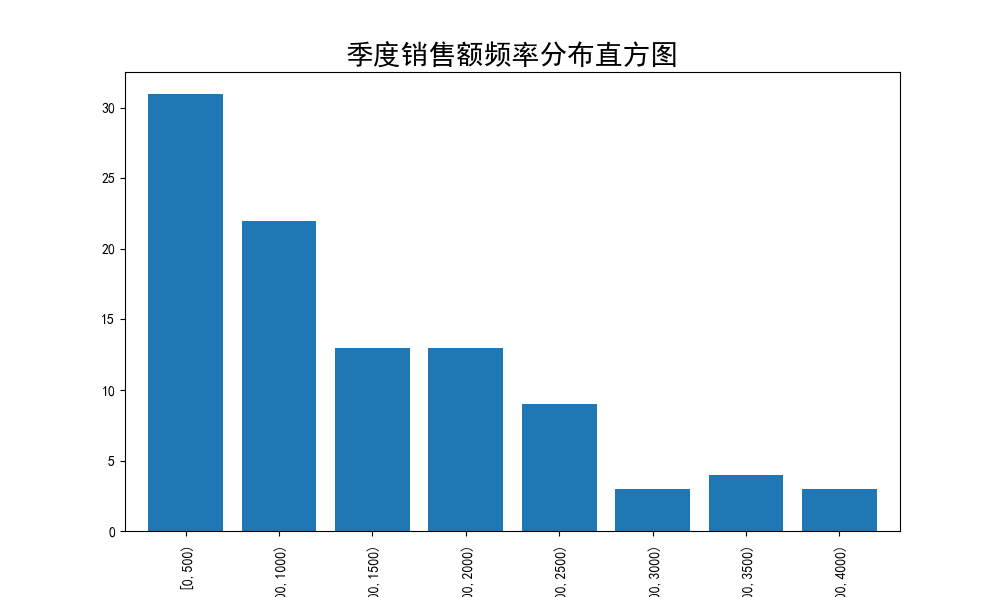
定性数据
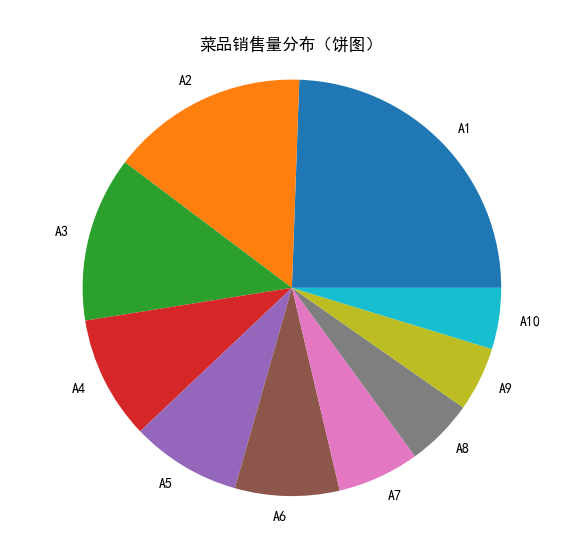
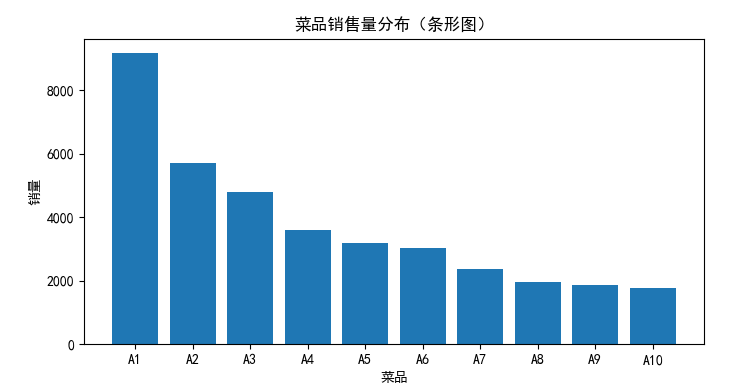
对比分析
-
对比分析是把两个相互联系的指标进行比较,从数量上展示和说明研究对象规模的大小、水平的高低、速度的快慢以及各种关系是否协调。
-
对比分析特别适用于指标间的横纵向比较、时间序列的比较。
-
选择合适的对比标准
-
对比分析的两种形式:
-
绝对数比较
-
相对数比较:它是由有联系的指标对比计算的,是用以反映客观现象之间数量联系程度的综合指标,其数值表现为相对数。
-
结构相对数:将统一总体内的部分数值与全部数值进行对比求得比重,用以说明事物的性质、结构或质量。如,居民食品支出额占消费支出总额的比重、产品合格率等。
-
比例相对数:将同一总体内不同部分的数值进行比较,表明总体内各部分的比例关系。如人口性别比例、投资与消费比例等。
-
比较相对数:将同一时期两个性质相同的指标数值进行比较,说明同类现象在不同空间条件下的数量对比关系。如不同地区的商品价格对比,不同行业、不同企业间某项指标对比等。
-
强度相对数:将两个性质不同但有一定联系的总量指标进行对比,用以说明现象的强度、密度和普遍程度,如人均国内生产总值用“元/人”表示,人口密度用“人/平方公里”表 示。
-
计划完成程度相对数:将某一时期实际完成数与计划数进行对比,用以说明计划完成程度。
-
动态相对数:将同一现象在不同时期的指标数值进行比较,用以说明发展方向和变化速度。如发展速度、增长比例等。
-
-
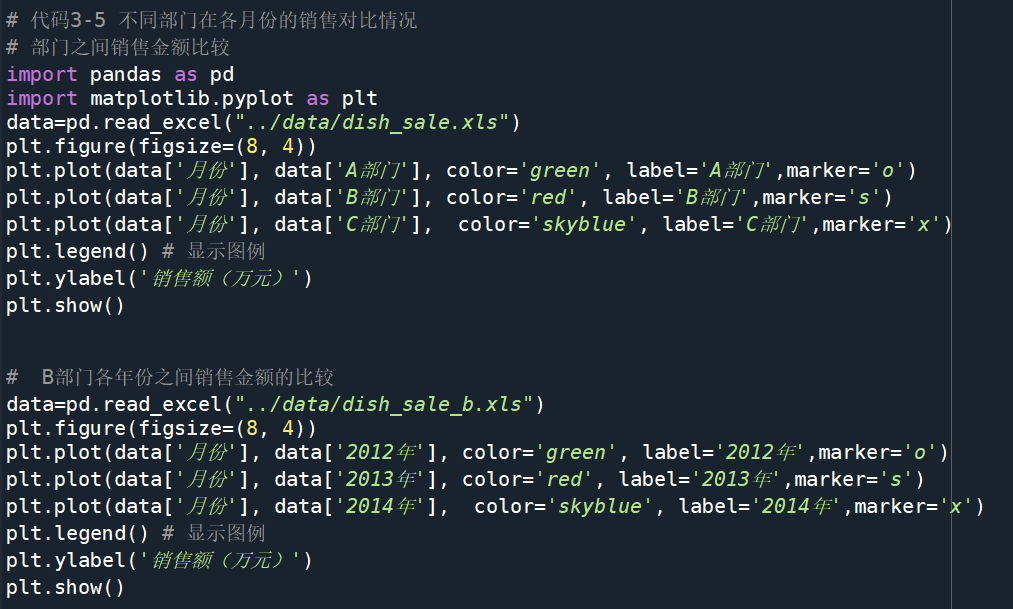
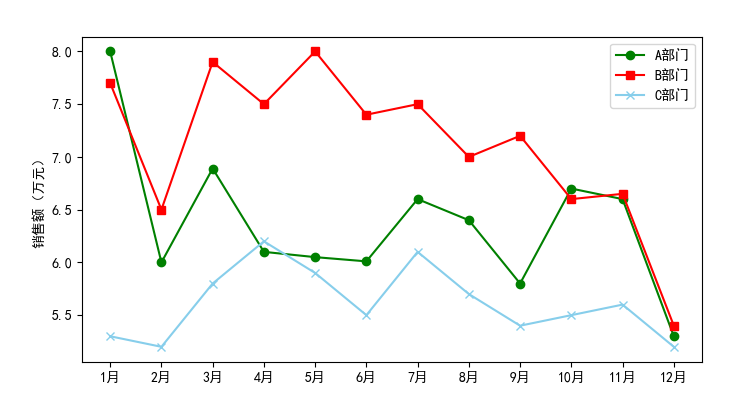
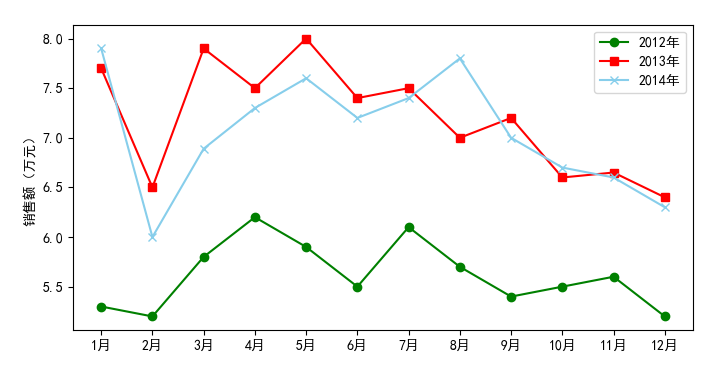
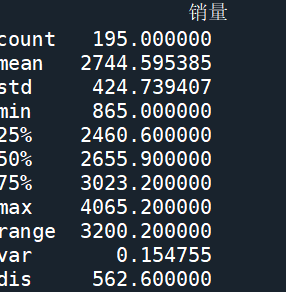
统计量分析
用统计指标对定量数据进行统计描述,常从集中趋势和离中趋势进行分析。
- 集中趋势度量
- 均值、中位数和众数
- 离中趋势度量
- 极差、标准差、变异系数、四分位数间距
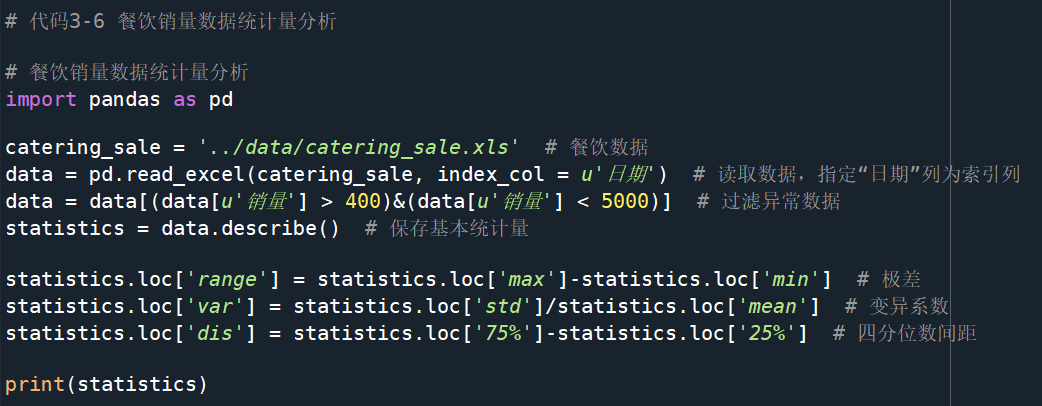
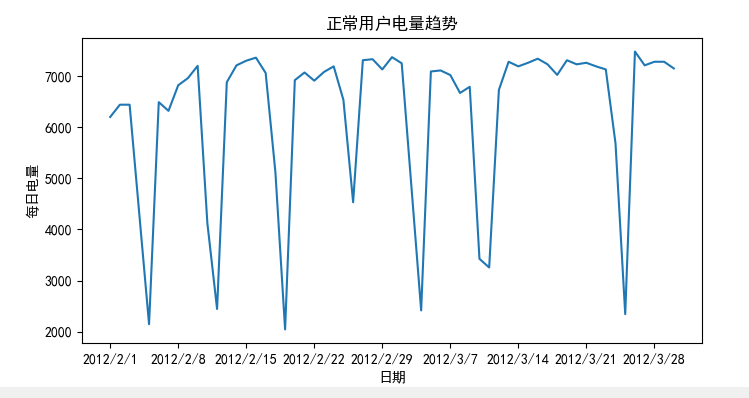
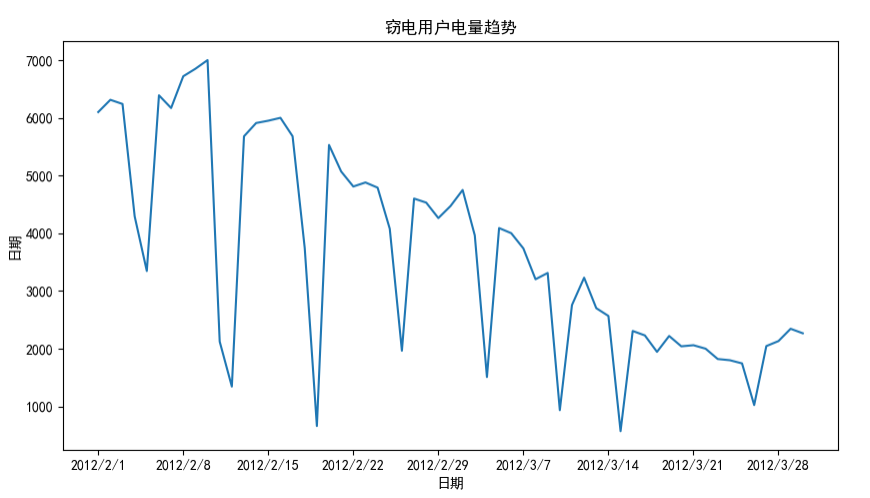
周期性分析
周期性分析时探索某个变量是否随着时间的变化而呈现出某种周期变化趋势。
- 年度性、季节性周期性趋势
- 月、周、天、小时周期性趋势
贡献度分析
贡献度分析又称为帕累托分析,他的原则是帕累托法则,又称20/80法则。
- 同样的投入在不同的地方会产生不同的效益。如对一个公司来说,80%的利润常常来自20%最畅销的产品,而其他80%的产品只产生了20%的利润。
- 因此,我们应该重点改善盈利最高的80%的产品。
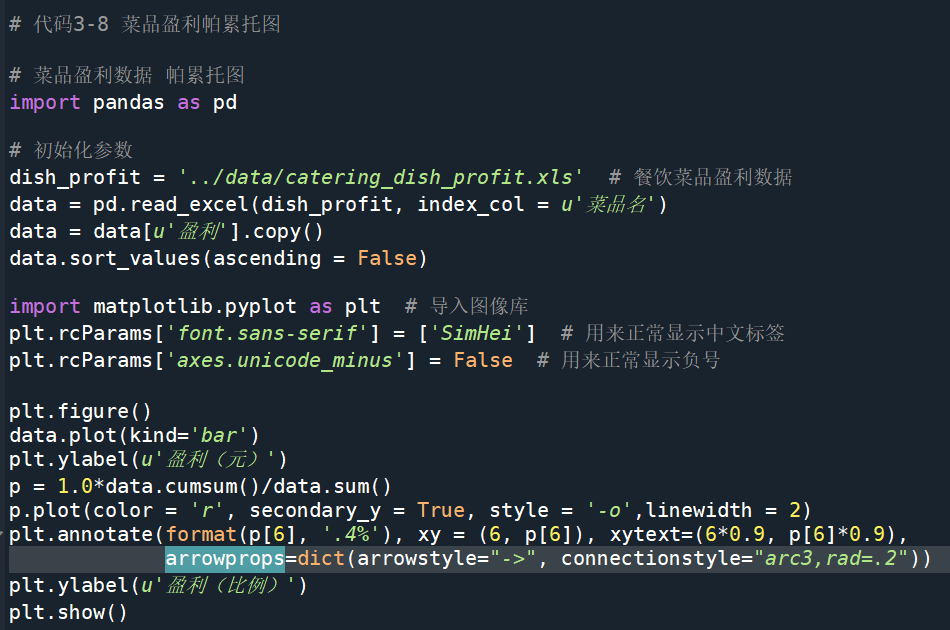
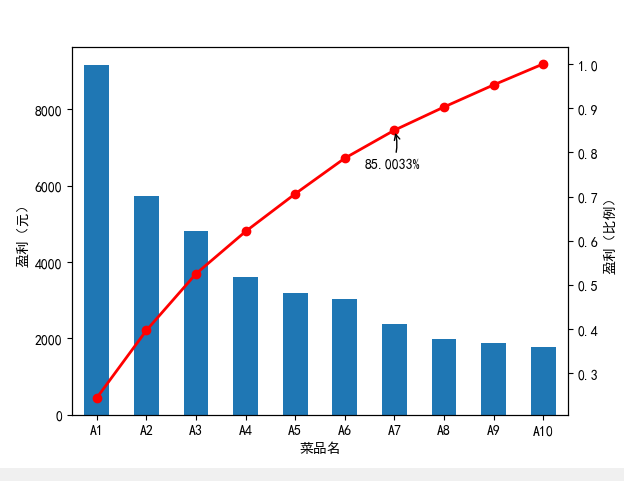
A1-A7七个菜品占了菜品种类的70%,总营业额占了85%。根据帕累托原则,应该增加对菜品A1-A7的成本投入,减少A8-A10的成本投入,以获的更高的盈利额。
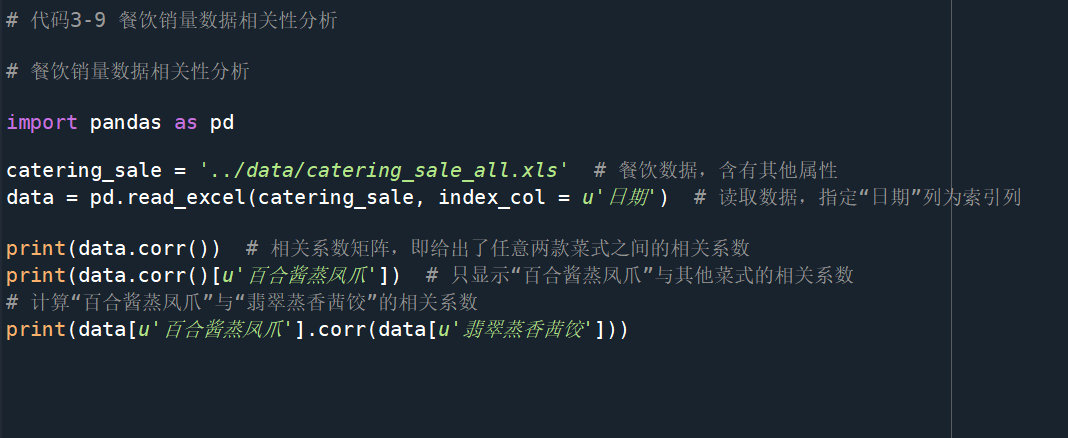
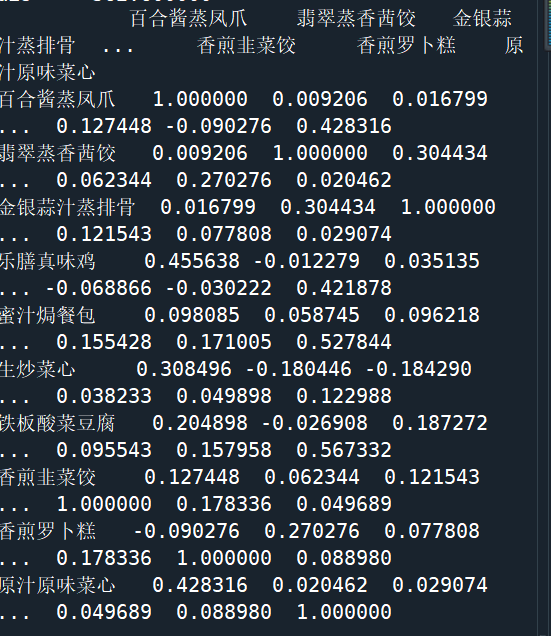
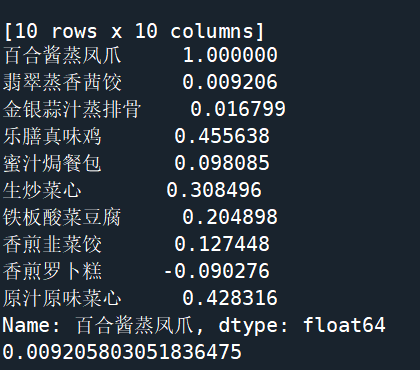
相关性分析
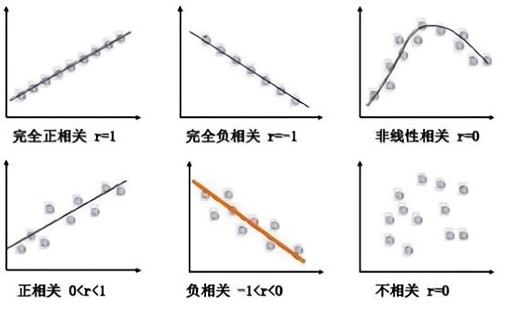
分析连续变量之间相关程度的强弱,并用适当的统计指标表示出来的过程称为相关分析:
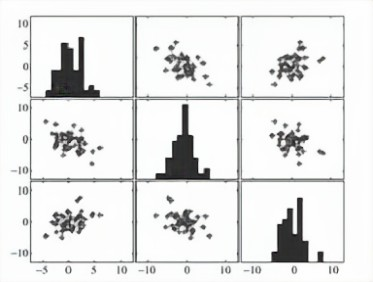
- 直接绘制散点图
- 绘制散点图矩阵
- 计算相关系数
- Pearson相关系数
- Spearman秩相关系数
- 判定系数