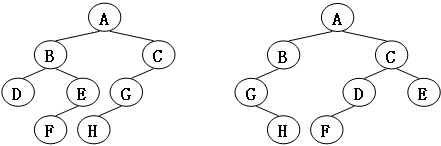
---

题意：给出两棵同构的有根树，同构修改点的标号使得两棵树完全一样，至少需要修改多少次。

分析：肯定是将子树和另外一棵的某个子树对应，而两棵子树的问题是一个子问题，显然只有同构的子树才可以对应，这要用到 树hash 来判断同构。

树hash 形如：$hash[u]=\sum _{v\in son[u]}hash[v]\ast prime[son\_size[v]]+1$，通过 hash 值可以在不管标号的情况下唯一确定一棵树的形态。

转移显然是一个匹配问题，要使得匹配后代价和最小，可以用最小费用最大流。

注：如果求解的是两棵同构子树最少需要修改的次数使得他们相同，只能过94%，如果求解的是两棵同构子树最多相同的部分，才可以 AC

---

代码：

#include <bits/stdc++.h>
#include <stdio.h>
#include <string.h>
#define M 505
#define inf 0x3f3f3f3f
#define pii pair<int,int>
#define fir first
#define sec second
typedef long long ll;
const int maxn = 1010;
const int mod = 998244353;
using namespace std;
bool ispri[maxn * 10];
int pri[maxn * 10], n, dp[maxn][maxn], s, t;
struct MCMF {struct node{int v,c,w,rev;		//rev 是 反向弧(u,v)，v 在 u 的位置。node(int vi = 0,int ci = 0,int wi = 0,int ri = 0) {v = vi;c = ci;w = wi;rev = ri;}};int dis[maxn],h[maxn],preV[maxn],preE[maxn];vector<node> g[maxn];vector<int> pot;			//点集 void init() {for(int i = 0; i < maxn; i++) g[i].clear();}void clear() {for (auto it : pot)g[it].clear(), h[it] = preV[it] = preE[it] = 0;pot.clear();}void add(int u,int v,int c,int w) {g[u].push_back(node(v,c,w,(int)g[v].size()));g[v].push_back(node(u,0,-w,(int)(g[u].size() - 1)));}int maxflow(int s,int t,int flow = inf) {int ans = 0,f = 0;/*fill(h,h + t + 1,0);fill(preV,preV + t + 1,0);fill(preE,preE + t + 1,0);*/while(flow) {priority_queue<pii,vector<pii>,greater<pii> > q;for (auto it : pot)dis[it] = inf;	//	fill(dis,dis + t + 1,inf);dis[s] = 0;q.push(pii(dis[s],s));while(!q.empty()) {pii now = q.top();q.pop();int u = now.sec;if(dis[u] < now.fir) continue;for(int i = 0; i < g[u].size(); i++) {int v = g[u][i].v,c = g[u][i].c,w = g[u][i].w;if(c && dis[v] > w + dis[u] + h[u] - h[v]) {preV[v] = u;preE[v] = i;dis[v] = w + dis[u] + h[u] - h[v];q.push(pii(dis[v],v));}}}		if(dis[t] == inf) break;	for (auto it : pot)	h[it] += dis[it];//for(int i = 0; i <= t + 1; i++) h[i] += dis[i];int mx = inf;for(int i = t; i != s; i = preV[i])mx = min(mx,g[preV[i]][preE[i]].c);flow -= mx; f += mx; ans += h[t] * mx;for(int i = t; i != s; i = preV[i]) {g[preV[i]][preE[i]].c -= mx;g[i][g[preV[i]][preE[i]].rev].c += mx;}}return -ans;}	
} p;
struct tree {vector<int>	g[maxn];int son[maxn], val[maxn], root;void add(int u,int v) {g[u].push_back(v);}void dfs(int u) {son[u] = 1; val[u] = 1;for (auto it : g[u]) {dfs(it);son[u] += son[it];val[u] = (val[u] + 1ll * val[it] * pri[son[it]] % mod) % mod;}}
} T[2];
void sieve(int n) {ispri[1] = ispri[0] = true;pri[0] = 0;for (int i = 2; i <= n; i++) {if (!ispri[i])pri[++pri[0]] = i;for (int j = 1; j <= pri[0] && i * pri[j] <= n; j++) {ispri[i * pri[j]] = true;if (i % pri[j] == 0) break;}}
}
int solve(int i,int j) {for (auto x : T[0].g[i]) {for (auto y : T[1].g[j]) {if (T[0].val[x] == T[1].val[y])dp[x][y] = solve(x,y);}}for (auto x : T[0].g[i])p.add(s,x,1,0), p.pot.push_back(x);for (auto y : T[1].g[j])p.add(n + y,t,1,0), p.pot.push_back(n + y);for (auto x : T[0].g[i]) {for (auto y : T[1].g[j]) {if (T[0].val[x] == T[1].val[y])p.add(x,n + y,1,-dp[x][y]);}}p.pot.push_back(s);p.pot.push_back(t);int ans = p.maxflow(s,t) + (i == j);p.clear();return ans;
}
int main () {sieve(5000);scanf("%d",&n);s = 2 * n + 2, t = 2 * n + 1;for (int i = 1, f; i <= n; i++) {scanf("%d",&f);if (f == 0) T[0].root = i;else T[0].add(f,i);}for (int i = 1, f; i <= n; i++) {scanf("%d",&f);if (f == 0) T[1].root = i;else T[1].add(f,i);}T[0].dfs(T[0].root);T[1].dfs(T[1].root);printf("%d\n",n - solve(T[0].root,T[1].root));return 0;
}