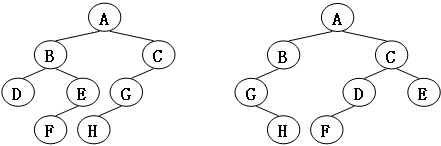
哈希算法在判定树同构方面的应用（上）

（一）需要掌握的前置知识：

（1）素数筛法：埃氏筛或者欧拉筛均可以。
以下为欧拉筛：

const int maxn=100100;
int p[maxn],cnt=0;
bool ha[maxn];
void Prime(void)
{ha[1]=true;for(int i=2;i<maxn;i++){if(!ha[i]) p[++cnt]=i;for(int j=1;j<=cnt&&i*p[j]<maxn;j++){ha[i*p[j]]=true;if(i%p[j]==0) break;}}
}

（2）一般的哈希知识。

（3）基本的树上 $dfs$ 遍历整棵树。

（4）树上重心的求解：

树的重心： 找到一个点 $x$, 以点 $x$ 为根时，其所有的子树中最大的子树节点数最少,那么这个点 $x$ 就是这棵树的重心。（以重心为根时，最大子树最小）

性质：
（1）树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，他们的距离和一样。（这里树的边权都定义为 $1$）
（2）把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
（3）一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
（4）一棵树最多有两个重心，且相邻。
（5）删除重心后所得的所有子树，节点数不超过原树的1/2。

其他说明：判定树同构有多种方法，且树同构的哈希也有多种方法，接下来仅介绍一种常用的哈希方法，其他的哈希方法类推即可。

（二）例题一：洛谷–P5043 【模板】树同构（[BJOI2015]树的同构）

题目连接

题面截图：

题意：

给定 $M$ 棵无根树，对于第 $i$ 棵无根树寻找 $1-i$ 中与第 $i$ 棵无根树同构的最小的无根树的编号。

题解：

根据题意，我们很容易写出伪代码：

for(int i=1;i<=m;i++)
{for(int j=1;j<=i;j++){if(第 i 棵树与第 j 棵树同构) //找到与第 i 棵树同构的树{printf("%d\n",j);break;}}
}

 
现在问题的关键转化为判断两棵无根树是否同构。
 
 
先来考虑问题的简化版：两个有根树如何判定是否同构。

类似于字符串的哈希，我们给树的每个节点附一个权值，记为$f[x]$

我们设 $f[x]=1+\sum _{y\in so{n}_x}f[y]\ast p[si[y]]$。这里 $f[x]$ 取自然溢出，即对 $2^{64}$ 取模。

其中 $y\in so{n}_x$ 表示在有根树中 $y$ 是 $x$ 的儿子节点。$f[y]$ 是 $y$ 的 $f$ 函数。

$p$ 数组是我们取前 $k$ （$k>=si[root]$）个质数，再随机打乱后的数组。
随机打乱 $p$ 数组。

random_shuffle(p+1,p+k+1);//k可以自己选定

$si[x]$ 表示 $x$ 子树的大小。

那么如果判定两个有根树同构呢，我们认为 如果$f[root1]=f[root2]$，那么就可以认为两棵树同构。事实上虽然 $f[root1]=f[root2]$ 有可能两棵树不一定同构，如果在确认算法正确且时间允许的情况下，我们可以多哈希来判定树的同构。事实上多哈希来判定同构，冲突的概率就极低了，数据一般也不容易构造。

现在我们来总结一下怎样判定两棵根分别为 $root1,root2$ 的树的同构的方法：
（1）求解 $p$ 数组，利用埃氏筛或者欧拉筛。
（2）在树上进行 $dfs$ 求解 $f$ 数组
（3）比较 $f[root1]$ 与 $f[root2]$

 
 
 
现在来考虑如何判定两棵无根树是否同构：
假设我们现在有两棵无根树 $A,B$ 同构，那么我们在 $A$ 树中选一点 $x$ 作为 $A$ 树的根，那么在 $B$ 树中一定存在一点 $y$，使得 $B$ 树以 $y$ 为根与 $A$ 树以 $x$ 为根同构。

相反的，如果我们在 $A$ 树中选一点 $x$ 作为 $A$ 树的根，那么在 $B$ 树中如果存在一点 $y$，使得 $B$ 树以 $y$ 为根与 $A$ 树以 $x$ 为根同构，那么两棵 无根树 $A,B$ 同构。

我们对 $A$ 树中的某一点 $x$ ，去找在 $B$ 树中是否能存在一个点 $y$ ，使得 $B$ 树中以点 $y$ 为根的树与 $A$ 树中以点 $x$ 为根的树同构。

那么我们能得到判定无根树同构的算法：
对于 $A$ 树中的某一点 $x$，求出$A$ 树中以 $x$ 为根的 $f[x]$，然后在 $B$ 树中寻找，是否存在一点 $y$，使得 $B$ 树中以 $y$ 为根的 $f[y]$ 等于$A$ 树中以 $x$ 为根的 $f[x]$。若存在，则说明 $A,B$同构，否则不同构。

为了方便判别，我们可以有以下处理：

对于 $A$ 树的每个节点 $x$ ，求出 $A$ 树中以 $x$ 为根的 $f[x]$，将这些 $f[x]$ 保存至 $a$ 数组。
对于 $B$ 树的每个节点 $y$ ，求出 $B$ 树中以 $y$ 为根的 $f[y]$，将这些 $f[y]$ 保存至 $b$ 数组。

将 $a,b$ 两数组按照相同的排序规则排序 （都升序或者都降序），那么如果最终 $A,B$两棵树的节点数相同且 $a,b$ 两数组对应位置相同，那么认为 $A,B$ 两棵树同构。
 
 

回到本题：
我们对 $M$ 棵树，对于第 $i$ 棵树，我们保存下以 $x$ 为根的 $f[x]$ 值，记为 $ha[i][x]=f[x]$，然后再对 $ha[i]$ 数组进行排序。

判定两棵树是否同构的时候只需要比较两棵树的大小和 $ha[i],ha[j]$ 两个数组即可。

空间复杂度 $O(n^2)$ ，时间复杂度 $O(n^3)$。(因为 $n$ 和 $m$ 同级别，就都当作 $n$ 来计算)

因为这里节点数 $n$ 比较小，所以我们直接打质数表即可。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<queue>
#define ll long long
#define pr make_pair
#define pb push_back
#define lc (cnt<<1)
#define rc (cnt<<1|1)
using namespace std;
const int inf=0x3f3f3f3f;
const ll lnf=0x3f3f3f3f3f3f3f3f;
const double dnf=1e15;
const int mod=1e9+7;
const int maxn=55;
int head[maxn],ver[maxn<<1],nt[maxn<<1];
int n[maxn],si[maxn],tot=1;
unsigned ll ha[maxn][maxn],f[maxn];
int p[]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229};void init(void)
{memset(head,0,sizeof(head));tot=1;
}void add(int x,int y)
{ver[++tot]=y,nt[tot]=head[x],head[x]=tot;
}void dfs(int x,int fa)
{f[x]=si[x]=1;for(int i=head[x];i;i=nt[i]){int y=ver[i];if(y==fa) continue;dfs(y,x);f[x]+=f[y]*p[si[y]];si[x]+=si[y];}
}bool check(int i,int j)
{for(int k=1;k<=n[i];k++){if(ha[i][k]!=ha[j][k]) return false;}return true;
}int main(void)
{random_shuffle(p+1,p+50+1);int m,fa;scanf("%d",&m);for(int i=1;i<=m;i++){init();scanf("%d",&n[i]);for(int j=1;j<=n[i];j++){scanf("%d",&fa);if(fa) add(fa,j),add(j,fa);}for(int j=1;j<=n[i];j++){dfs(j,0);ha[i][j]=f[j];}sort(ha[i]+1,ha[i]+n[i]+1);}for(int i=1;i<=m;i++){for(int j=1;j<=i;j++){if(n[i]==n[j]&&check(i,j)){printf("%d\n",j);break;}}}return 0;
}

 
 
 
 
虽然 $O(n^3)$ 的算法足够通过本题，但是如果 $n=5e3$ 级别的就不能再处理了，考虑优化。

思考：我们为什么要求第 $i$ 棵无根树分别以每个节点 $x$ 为根的 $f[x]$ ?

因为 两棵无根树$A,B$ 同构 等价于 对于$A$ 中以某一点 $x$为根的有根树， $B$ 中存在以 $y$ 为根的有根树与 $A$ 中以 $x$ 为根的有根树同构。我们需要在 $B$ 中找到 $y$ 。

那么我们能不能快速在$A,B$中分别找到一点 $x,y$，使得 $x,y$ 是相对应的，即 让 $A,B$ 是否同构等价于以$x$为根的有根树与以$y$为根的有根树是否同构。

能不能找到这样的两点 $x,y$ 呢？ 重心！重心！重心！

于是判定同构的条件转化为：
两棵无根树 $A,B$ 是否同构，等价于他们以重心为根的有根树是否同构。

考虑一下为什么？若重心唯一，那么两棵无根树 $A,B$ 同构时的重心必定对应；若重心都不唯一，那么两棵无根树 $A,B$ 同构时两棵树的重心也一一对应。

即，若两棵树同构，那么重心为根的树一定是同构的。如果重心为根的树是同构的，那么两棵树一定是同构的。

那么求解无根树是否同构的方法可以优化为以下做法：
（1）求解树 $A,B$ 的重心，重心至多有两个。
（2）求解树 $A,B$ 以重心为根的 $f$。
（3）判断是否同构。

回到本题：
我们只需要求解第 $i$ 棵树的重心，然后求解重心的 $f$ 即可。

空间复杂度 $O(n)$，时间复杂度 $O(n^2)$

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#include<queue>
#include<bitset>
#include<map>
#include<unordered_map>
#include<unordered_set>
#include<set>
#include<ctime>
#define ui unsigned int
#define ll long long
#define llu unsigned ll
#define ld long double
#define pr make_pair
#define pb push_back
#define lc (cnt<<1)
#define rc (cnt<<1|1)
#define len(x)  (t[(x)].r-t[(x)].l+1)
#define tmid ((l+r)>>1)
#define fhead(x) for(int i=head[(x)];i;i=nt[i])
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
using namespace std;const int inf=0x3f3f3f3f;
const ll lnf=0x3f3f3f3f3f3f3f3f;
const double dnf=1e18;
const double alpha=0.75;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1.0);
const int hp=13331;
const int maxn=55;
const int maxm=100100;
const int maxp=100100;
const int up=1100;
int head[maxn],ver[maxn<<1],nt[maxn<<1];
int n[maxn],si[maxn],dp[maxn],tot=1,rt1,rt2,nown;
llu f[maxn],rt1f[maxn],rt2f[maxn];
int p[]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229};void init(void)
{memset(head,0,sizeof(head));tot=1;rt1=0,rt2=0;
}void add(int x,int y)
{ver[++tot]=y,nt[tot]=head[x],head[x]=tot;
}void dfs1(int x,int fa)
{si[x]=1,dp[x]=0;for(int i=head[x];i;i=nt[i]){int y=ver[i];if(y==fa) continue;dfs1(y,x);si[x]+=si[y];dp[x]=max(dp[x],si[y]);}dp[x]=max(dp[x],nown-si[x]);if(rt1==0||dp[x]<dp[rt1]) rt1=x,rt2=0;else if(dp[x]==dp[rt1]) rt2=x;
}void dfs2(int x,int fa)
{f[x]=si[x]=1;for(int i=head[x];i;i=nt[i]){int y=ver[i];if(y==fa) continue;dfs2(y,x);f[x]+=f[y]*p[si[y]];si[x]+=si[y];}
}bool check(int i,int j)
{return (rt1f[i]==rt1f[j]&&rt2f[i]==rt2f[j])||(rt1f[i]==rt2f[j]&&rt2f[i]==rt1f[j]);
}int main(void)
{random_shuffle(p+1,p+50+1);int m,fa;scanf("%d",&m);for(int i=1;i<=m;i++){init();scanf("%d",&n[i]);for(int j=1;j<=n[i];j++){scanf("%d",&fa);if(fa) add(fa,j),add(j,fa);}nown=n[i];dfs1(1,0);if(rt1!=0) dfs2(rt1,0),rt1f[i]=f[rt1];if(rt2!=0) dfs2(rt2,0),rt2f[i]=f[rt2];}for(int i=1;i<=m;i++){for(int j=1;j<=i;j++){if(check(i,j)){printf("%d\n",j);break;}}}return 0;
}