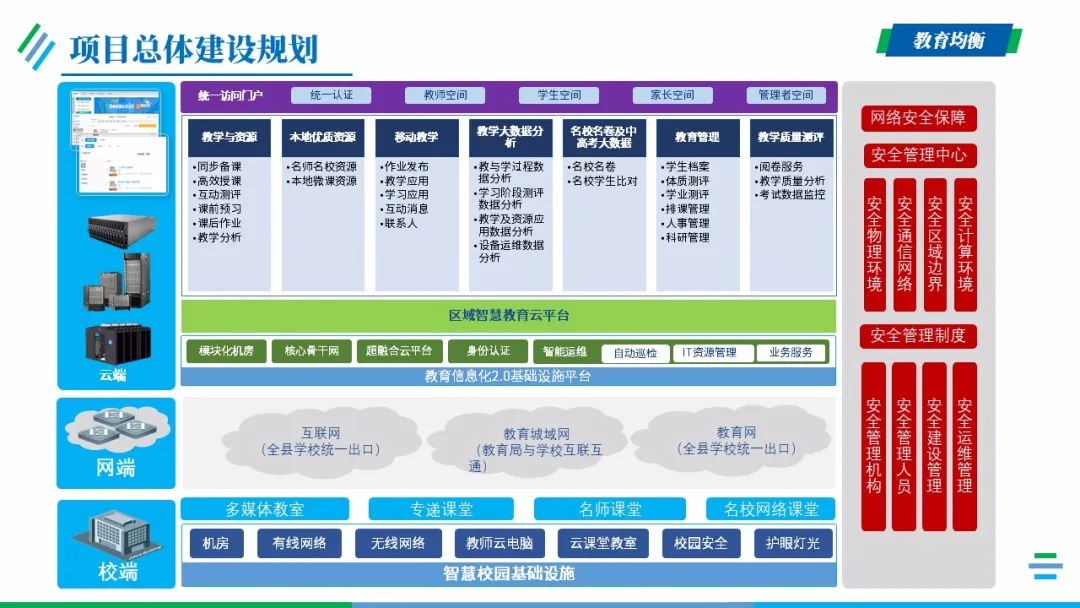
项目概述

“人才决定未来，教育成就梦想”。我国一直坚持不懈推进教育信息化，努力以信息化为手段扩大优质教育资源覆盖面。我国规划将通过教育信息化，逐步缩小区域、城乡数字差距，大力促进教育公平，让亿万孩子同在蓝天下共享优质教育、通过知识改变命运。

教育部于2018年颁布了“教育信息化2.0行动计划”，通过实施教育信息化2.0行动计划，到2022年基本实现“三全两高一大”的发展目标，即教学应用覆盖全体教师、学习应用覆盖全体适龄学生、数字校园建设覆盖全体学校，信息化应用水平和师生信息素养普遍提高，建成“互联网+教育”大平台。

在“中国教育现代化2035”规划中明确要求实现基本公共教育服务均等化。提升义务教育均等化水平，建立学校标准化建设长效机制，推进城乡义务教育均衡发展。在实现县域内义务教育基本均衡基础上，进一步推进优质均衡。推进随迁子女入学待遇同城化，有序扩大城镇学位供给。完善流动人口子女异地升学考试制度。实现困难群体帮扶精准化，健全家庭经济困难学生资助体系，推进教育精准脱贫。办好特殊教育，推进适龄残疾儿童少年教育全覆盖，全面推进融合教育，促进医教结合。

为贯彻落实全国教育大会精神，确保新时代教育现代化建设开好局、起好步制定的“加快推进教育现代化实施方案（2018－2022年）”中，着力构建基于信息技术的新型教育教学模式、教育服务供给方式以及教育治理新模式。促进信息技术与教育教学深度融合，支持学校充分利用信息技术开展人才培养模式和教学方法改革，逐步实现信息化教与学应用师生全覆盖。

义务教育优质均衡是为了巩固义务教育基本均衡发展成果，进一步缩小义务教育城乡和校际差距，推进义务教育更高水平发展，全面提高义务教育质量建立的评估制度。

教育信息化是指在教育领域全面深入地运用现代信息技术来促进教育改革与发展，全面促进教育公平化、解决城乡差异，促进优质教育资源向贫困、偏远地区输送，提高当地的教育质量和水平，促进教育均衡发展。

教育信息化优质均衡是以教育信息化为抓手，充分利用信息化技术的数字化、网络化、智能化和多媒体化，突破时空限制和技术壁垒， 全面实现优质学校资源、优秀教师资源、丰富的素材资源于一体，实现资源的跨区、跨校传播和分享，解决资源分布不平衡的现状。从而能更高效、高质、均衡的推进义务教育向更高水平的发展。

县域教育信息化优质均衡建设

本文主要内容：

• 背景概述

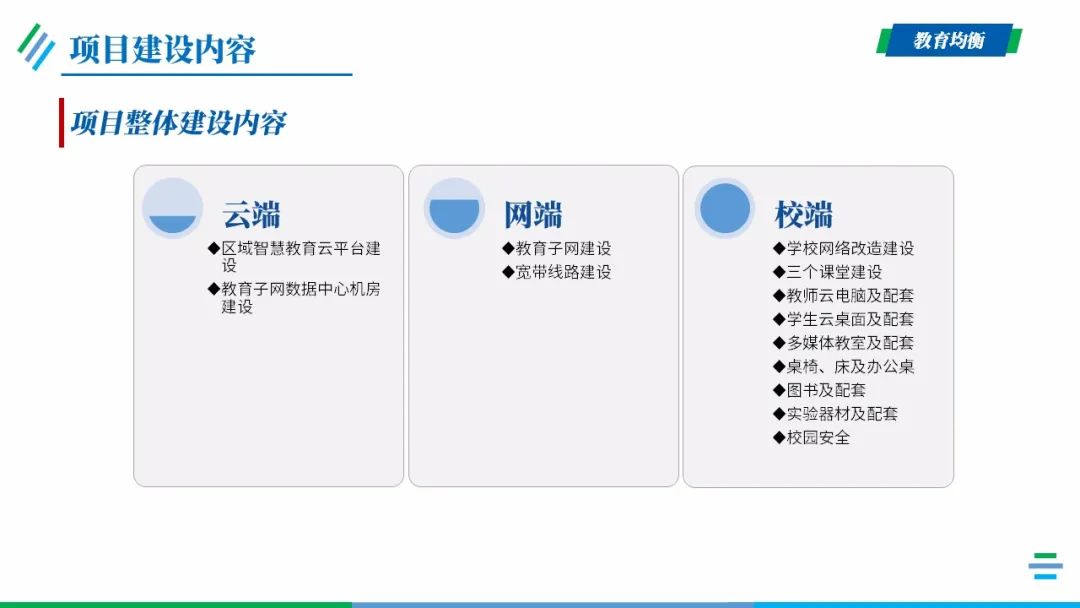
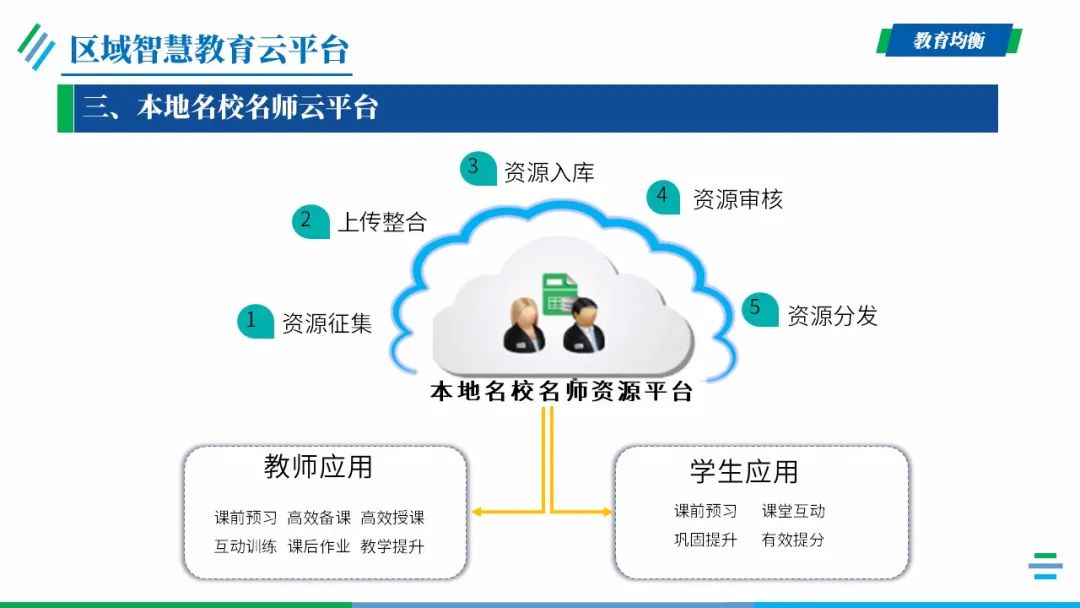
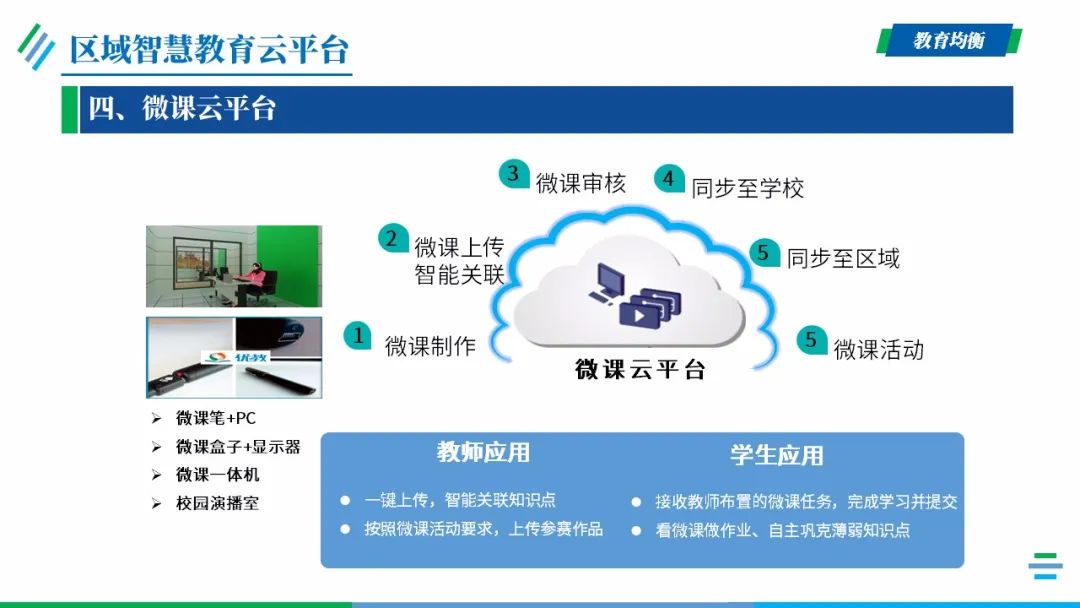
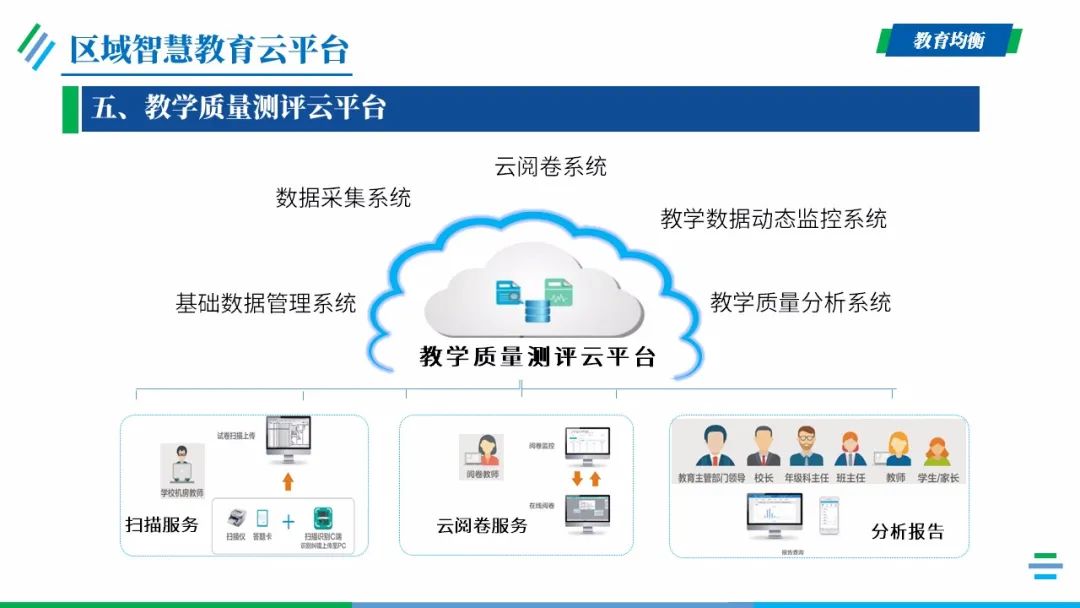
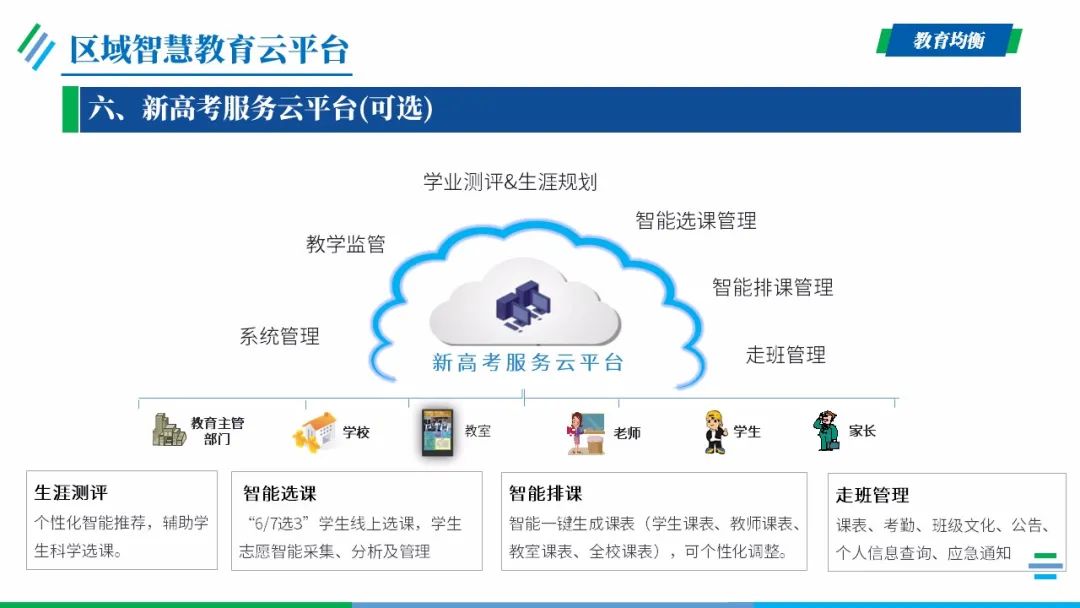
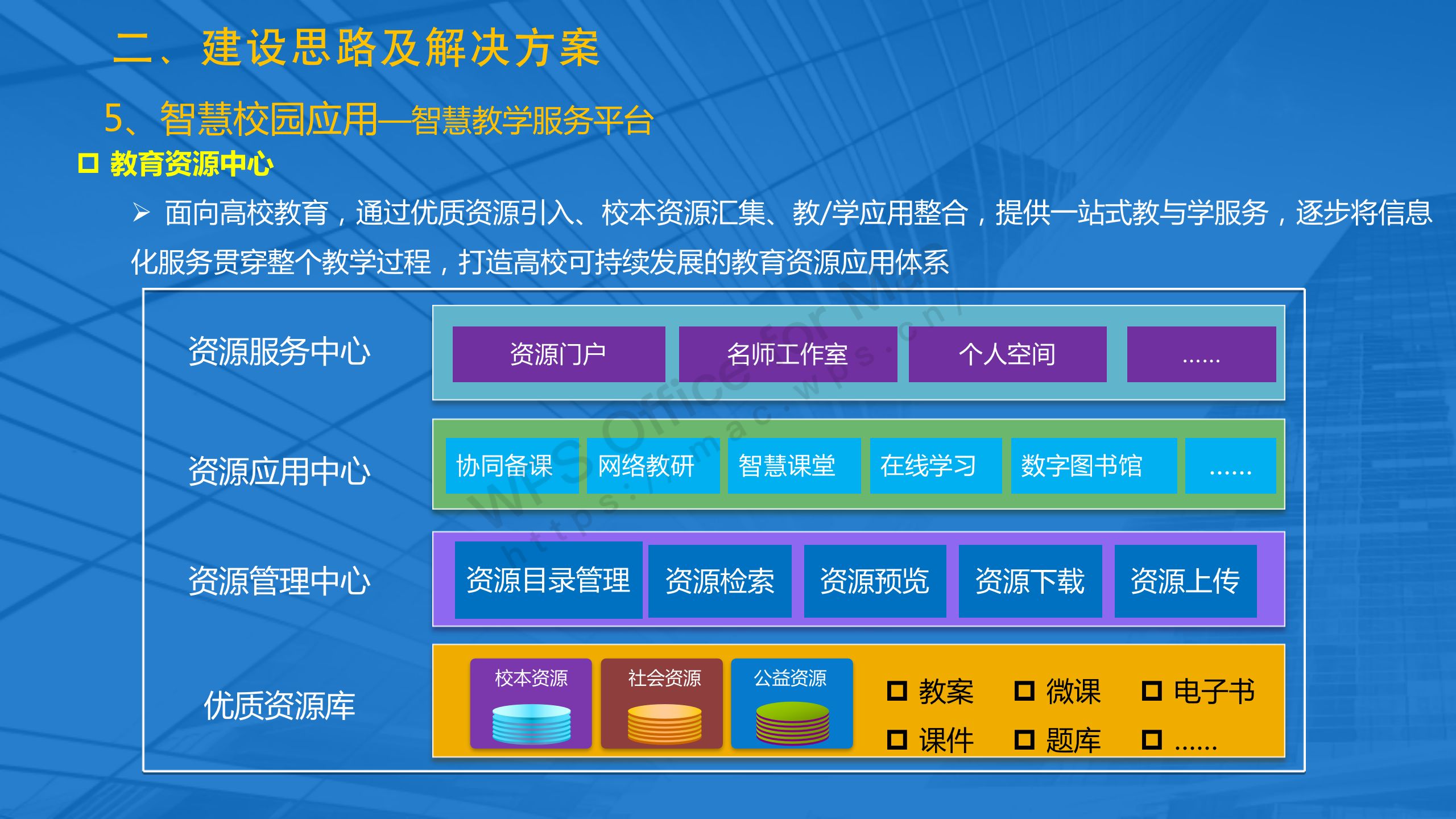
• 项目建设内容

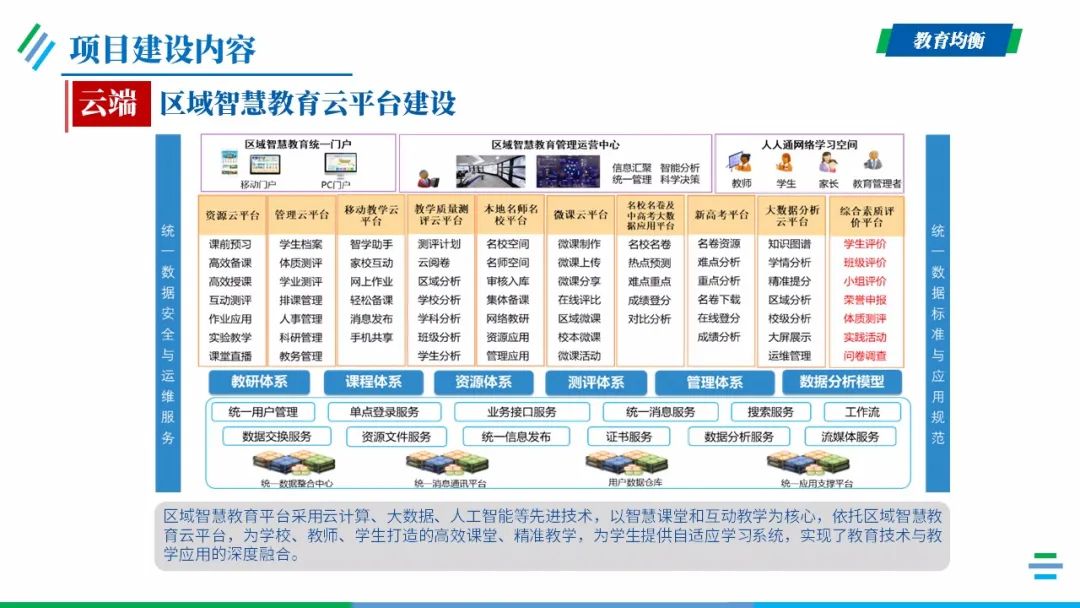
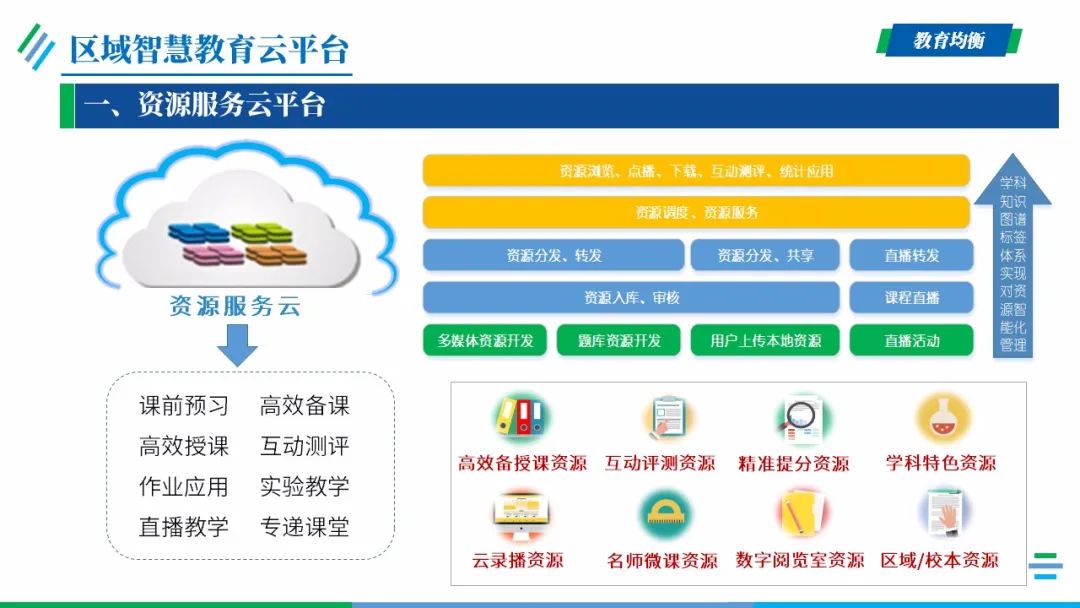
  云端

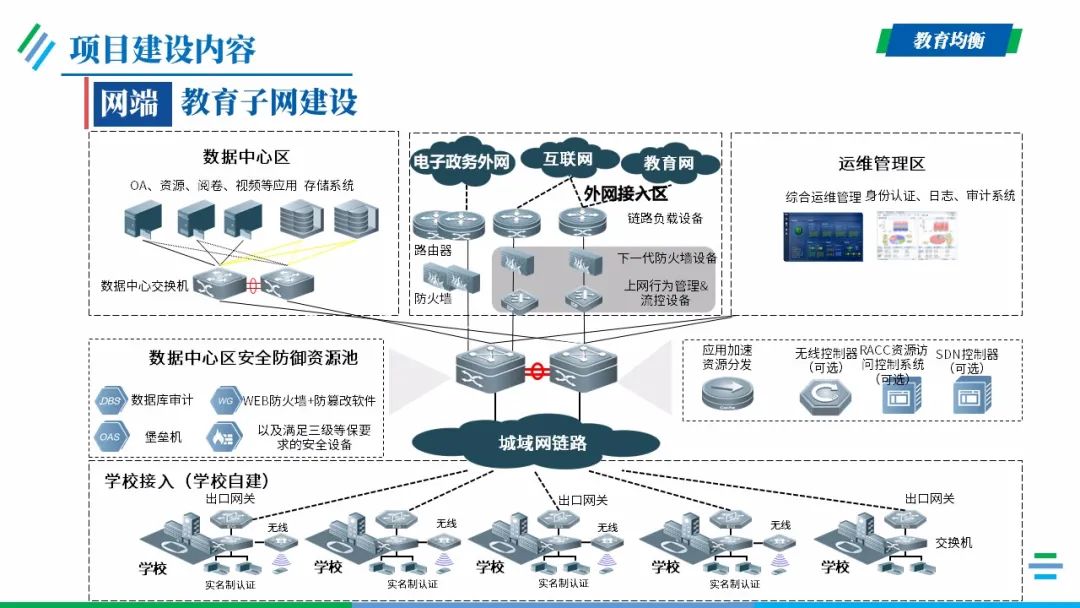
  网端

  校端

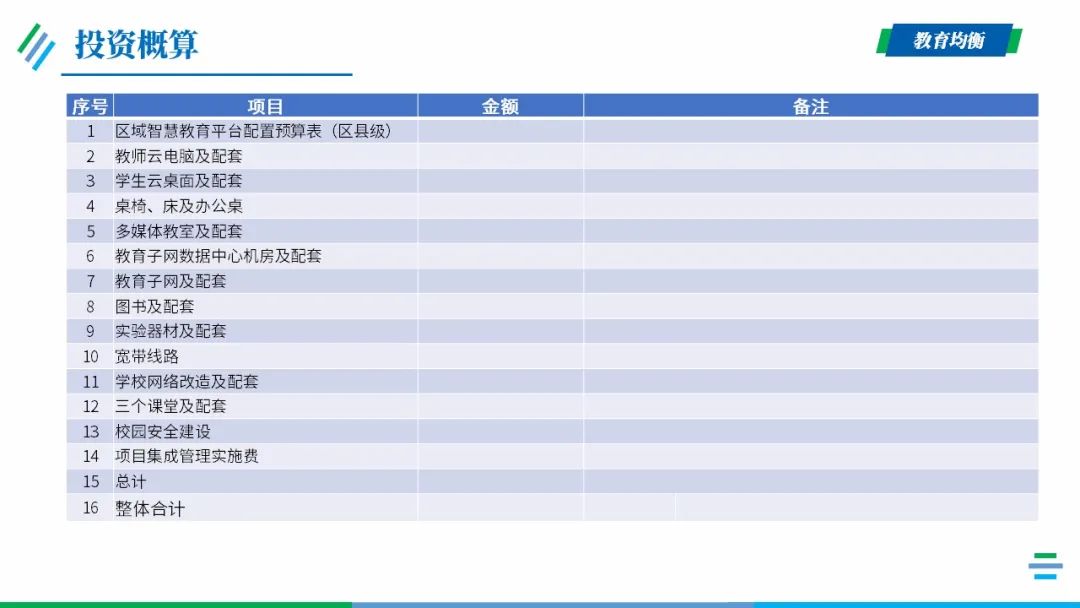
• 项目投资概算

• 项目建设必要性