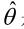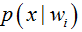【概率论】极大似然估计和最大后验估计

1.前言

2 频率学派和贝叶斯学派

2.1 频率学派

2.2 贝叶斯学派

3. 极大似然估计

3.1 概率和似然

3.2 极大似然原理及求解

3.3 例题

4. 最大后验估计

4.1 最大后验估计原理

5. 参考

1.前言

极大似然估计和最大后验估计都是参数的估计方法，一定要记住，它的目标是对模型的参数 $\LARGE \theta$ 进行估计。

为什么一定要强调是模型参数的估计方法？

因为实际上（有监督的）机器学习的方法在训练和测试上完成的是两件事，这两件事是先后关系，也是有区分的。

第一件事（训练阶段）：参数估计。这是一个是统计过程，根据训练数据求得模型的参数。这一阶段模型的参数 $\LARGE \theta$ 是未知的，而训练的样本 $\LARGE (X,Y)$ 是已知的，其中 $\LARGE X$ 表示输入的训练样本、 $\LARGE Y$ 表示类别（或者说概率，因此知道概率就可以进行类别划分），目标是求解 $\LARGE \theta$ ，因此称为参数估计。

第二件事（测试、推理阶段）：预测，也称为概率预测。根据已经求得的模型参数 $\LARGE \theta$ 来进行样本的预测。最常见的逻辑回归就是根据输入样本，来求得样本类别。在这个阶段模型的参数 $\LARGE \theta$ 和输入的样本 $\LARGE X$ 是已知的，而样本的类别 $\LARGE Y$ 是未知的，是一个求概率的过程。

了解在不同阶段中 $\LARGE \theta$ 、 $\LARGE X$ 、 $\LARGE Y$ 的已知、未知情况，对于我们理解后面极大似然估计和最大后验估计非常有用。具体的情况将在后面详细阐述。

2 频率学派和贝叶斯学派

为了更通俗易懂的说明极大似然估计和最大后验估计，我们我们首先定义两个参数：

$\LARGE \theta$ ：表示事件发生的概率，或者产生某一事件的重要因素，是导致事件发生的原因。
$\LARGE x$ 或者 $\LARGE X$ ：是一个随机变量，表示某一事件发生的结果，或者说我们多次实验观测到的结果。

2.1 频率学派

频率学派认为, 一个事件发生的概率，也就是前面我们声明的参数 $\LARGE \theta$ ，虽然是未知的, 但是却是一个客观存在的固定值。

如何理解这句话呢？

就是说事件概率是一个确定的值，当进行大量实验时，该事件出现的频率就会趋于一个稳定的值，这个值就是事件的概率。频率学派的代表算法就是极大似然估计MLE。

这里举两个极大似然方法最经典的例子：

例子1：抛硬币。在抛硬币的事件中，正面向上的概率P就是参数 $\LARGE \theta$ ，现在我们为了求这个概率p，抛10次硬币，结果10次正面向上，那么根据极大似然方法，P就为1.0。

例子2：简单的抓球游戏。假如一个盒子里面有红黑共10个球，每次有放回的取出，取了10次，结果为7次黑球，3次红球，问黑球的个数。这个黑球的个数就是参数 $\LARGE \theta$ ，基于 $\LARGE \theta$ 的取值，我们多次拿取得到了7次黑球，3次红球的观测结果，即 $\LARGE X$ 。根据极大似然方法，黑球的数量为10个。

2.2 贝叶斯学派

贝叶斯学派则认为参数 $\LARGE \theta$ 也是一个随机变量, 它自身也服从一个先验分布，然后基于观测结果 $\LARGE X$ 来计算后验分布, 最后通过后验概率的最大化来确定参数自身的分布。

贝叶斯派的代表算法就是最大后验概率估计MAP，这种方法在先验假设比较靠谱的情况下效果显著，随着数据量的增加，先验假设对于模型参数的主导作用会逐渐削弱，相反真实的数据样例会大大占据有利地位。极端情况下，比如把先验假设去掉，或者假设先验满足均匀分布的话，那她和极大似然估计就如出一辙了。

可能有些人就会迷糊，逻辑回归就是假设服从伯努利分布，为什么采用的是概率学派的极大似然估计来求解呢？
逻辑回归是分类的结果Y服从伯努利分布，即认为类别1出现的概率为P，相应地，类别0出现的概率就为1-P，即认为这个P的值是客观存在的，因此可以根据实验结果利用极大似然估计来求解。而贝叶斯学派认为的是概率P本身也是随机变量，服从一定的分布，而非前面的Y。

3. 极大似然估计

3.1 概率和似然

在讲具体的极大似然估计前，首先来区分一下概率和似然。

似然（likelihood）这个词其实和概率（probability）是差不多的意思，Colins字典这么解释：The likelihood of something happening is how likely it is to happen. 你把likelihood换成probability，这解释也读得通。但是在统计里面，似然函数和概率函数却是两个不同的概念（其实也很相近就是了）。

在极大似然估计相关博文中，出现频率最高的就是这个公式：

公式的输入分别为参数 $\LARGE \theta$ 以及结果 $\LARGE x$ 。

根据 $\LARGE \theta$ 和 $\LARGE x$ 的已知或者未知的情况，该公式有两个不同的意义：

当 $\LARGE \theta$ 是已知的并且保持不变， $\LARGE x$ 是变量时，该公式描述的是在参数确定的情况下，某一事件（结果） $\LARGE x$ 出现的概率，是概率函数。
当 $\LARGE \theta$ 是变量， $\LARGE x$ 是已知的并且保持不变，该公式描述的是事件（结果）在不同 $\LARGE \theta$ 下出现的概率，是似然函数。在后面极大似然估计中，用到的是就是似然函数。在似然的意义下，还可以写成：，即用“；”代替“|”。一般情况下为了特别的区分似然函数和概率函数，都会采用后面的写法。

3.2 极大似然原理及求解

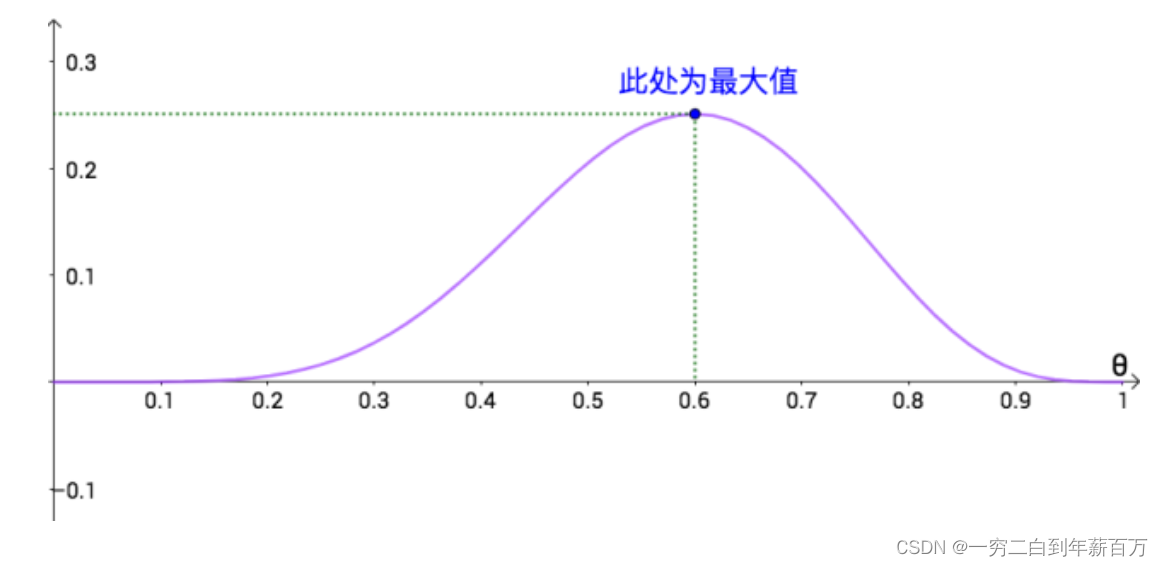
最大似然估计的目的就是：利用已知的数据分布 $\LARGE x$ ，反推出什么样的参数 $\LARGE \theta$ 才能使我们目前观测到结果出现的概率最大。

根据我们3.1所述，很明显就要让似然函数最大。

这里需要解释一下为什么在2.1中我们说极大似然估计法的前提是认为参数 $\LARGE \theta$ 是一个客观存在的固定值，而在3.1又说 $\LARGE \theta$ 是一个变量？

这两种说法实际上是不冲突的。因此极大似然的过程是求解 $\LARGE \theta$ 的过程，虽然我们认为 $\LARGE \theta$ 是固定的，但是我们还不知道它具体的取值。可以理解为，我们需要一次次输入 $\LARGE x$ 来计算 $\LARGE \theta$ ，只有使结果概率最大的 $\LARGE \theta$ 才是最终我们需要的。在这种情况下，我们每一次计算用的都是相同的 $\LARGE x$ ，即 $\LARGE x$ 是已知并且保持不变，每一次计算的 $\LARGE \theta$ 都不同，是变量。

这里给出极大似然估计法在离散型和连续情况下的定义。因为我们需要每一个样本对应的似然函数都最大，因此需要将它们相乘取最大。

求解的步骤如下：

3.3 例题

现在有一个黑箱子里面有标有1或2的球共100个，现在从中有放回的抽取10个球，结果为{1,2,2,2,1,2,1,1,2,2}，估计标有1的球在黑箱子里面有多少个。

问题的本质在于估计标号为1的球的个数，设其个数为 $\LARGE \theta$ 个，那么选中标号1的球的概率 p(x=1) = $\LARGE \theta$ /100，而实验结果我们可以得到：

$P = p^{4} *(1-p)^{6}$

之后对P取对数：

$ln(p)= 4ln(p) + 6ln(1-p)$

为了使对数值最大，求导求驻点：

$\frac{\partial l}{\partial p} = \frac{4}{p} - \frac{6}{1-p} = \frac{4-10p}{p(1-p)}$

算出 p = 0.4，即 $\LARGE \theta$ /100 = 0.4，那么 $\LARGE \theta$ =40

4. 最大后验估计

4.1 最大后验估计原理

仍然以我们2.1举的抛硬币的例，抛一枚硬币10次，有10次正面朝上，0次反面朝上。问正面朝上的概率p。在频率学派来看，利用极大似然估计可以得到 p= 1.0。但是很显然，一般情况下硬币都是均匀的。可以看到，当缺乏数据时极大似然估计可能会产生严重的偏差。

最大后验估计就可以在一定程度上解决这样的问题。

最大后验估计依然是根据已知样本 $\LARGE x$ ，通过调整模型参数 $\LARGE \theta$ 使得模型能够产生该数据样本的概率最大，只不过对于参数有了一个先验假设，即模型参数可能满足某种分布，不再一味地依赖数据样例（万一数据量少或者数据不靠谱呢）。

可以看到，最大后验估计认为 $\LARGE \theta$ 也是是一个随机变量，即 $\LARGE \theta$ 也具有某种分布，称为先验分布，记为。求解时除了要考虑似然函数之外，还要考虑的先验分布，认为使取最大值的才是最好的，此时要最大化的函数变为:

由于的先验分布 $\LARGE P(X)$ 是固定的（可通过分析数据获得，其实我们也不关心 $\LARGE X$ 的分布，我们关心的是 $\LARGE \theta$ ），因此最大化函数可变为：

因此最终最大化，是参数 $\LARGE \theta$ 的后验分布。

如何理解为 $\LARGE \theta$ 的后验分布？

在博文后验概率、全概率公式以及贝叶斯公式中，其中讲到由果求因就是后验概率。在这里我们细想一个例子：抓球实验，因为箱子的黑球和红球的数量（ $\LARGE \theta$ ）不同，因此我们才会在那么多次有放回的抽取的中得到不同的结果 $\LARGE X$ 。也就是 $\LARGE \theta$ 是产生我们这样一系列观测结果 $\LARGE X$ 的因，从这个角度来看确实是后验概率。

最大后验概率估计的公式表示如下：

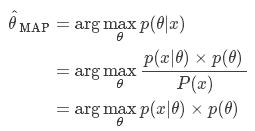
从上面公式可以看出， $p(x|\theta )$ 是似然函数，而 $p(\theta )$ 是先验概率。对其取对数：

通过MAP最终的式子不难看出，MAP就是多个作为因子的先验概率 $p(\theta )$ 。这个 $p(\theta )$ 可以是任何的概率分布，比如高斯分布。

5. 逻辑回归和极大似然

到目前为止，极大似然和最大后验估计的原理都已经讲的非常明确了。

极大似然估计：使似然函数最大，即最大化。由于参数 $\LARGE \theta$ 是是产生这样观测结果 $\LARGE x$ 的原因，因此可以简单的看成是：P(果|因)
最大后验估计：使 $\LARGE \theta$ 的后验概率最大，即最大化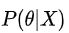，等价于最大化似然函数乘以先验概率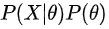。后验概率可以看成是由果索因：P(因|果)

上述情况只涉及到简单的对参数进行估计，而在实际中我们除了完成参数估计，还希望可以对未知样本进行预测。

现在我们来看一个机器学习的典型模型——逻辑回归，公式如下。在这里 $\LARGE x$ 并非前面所述的观测结果，而是输入的样本， $\LARGE \theta$ 表示逻辑回归的参数， $\LARGE y$ 表示样本的类别。

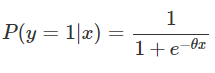
由于逻辑回归是一个二分类模型，因此对应的判别为类别0的概率就为：

进一步进行统一：

之后通过极大似然的方法进行参数估计：

这一切看起来都太丝滑了，似乎没有任何问题。但是很多博客中都将称为给定样本 $\LARGE x$ ，模型判别为为类别1的后验概率。既然是后验概率，那么对应的似然函数应该 $\LARGE P(x|y)$ 啊，那怎么就直接对构建似然函数了呢？

我们从两个方面来说明一下：

第一个方面：在概率模型的讲述中，很多都将称为是后验概率，难道这么称呼有错吗？当然没有，只不过他们都是从样本预测的角度来说明的，我们上面的公式也一样。在预测阶段，输入样本 $\LARGE x$ ，经过逻辑回归后得到样本的特征，此时样本的特征是结果，根据特征来判断样本属于哪个类别，是由果索因，因此可以看成是后验概率。

有些人可能会认为我们已知样本了特征，然后根据这些特征来求得样本的类别，是由因索果。

这样理解是搞错了特征，类别的因果关系。因为样本是客观存在的，它不会因为我们的观测方式（特征提取的方法）而改变，各类算法提取出的特征只是样本本质的体现。
因此实际上，样本的类别，是本质，是因，正因为有了这样的因，我们通过不同的观测（特征提取算法）才会得到不同的特征，即特征只是样本的在不同维度下体现，是果。

第二个方面：我引用博客的一段话：

个人认为用“因”“果”描述先验后验，不太合适。英文将先验概率P(x)描述为evidence，evidence有显性的意思在里面，如果用“显示的”“隐藏的”来描述，看是不是能顺畅点。

似然：P(显|隐)

后验：P(隐|显)

这也就是我们前言所讲的，真的铺垫了很久。在逻辑回归参数估计阶段，我们输入样本 $\LARGE x$ 和对应的类别 $\LARGE y$ ，这时候样本 $\LARGE x$ 和对应的类别 $\LARGE y$ 是已知的，是“显”，而模型的参数 $\LARGE \theta$ 是未知的，是“隐”。因此这么来看，似然函数不是，也不是 $\LARGE P(x|y)$ ，而是 $\LARGE P((x,y)|\theta )$ 。但是这个式子中 $\LARGE P(x,y)$ 往往表示 $\LARGE x$ ， $\LARGE y$ 的联合概率分布，是不准确的，因此准确来说似然函数是 $\LARGE P((y|x)|\theta )$ 。然后我们再来看一下前面似然函数的另一个写法：将’|‘变为'；'，因此 $\LARGE P((y|x)|\theta )$ 还可以写为 $\LARGE P((y|x);\theta)$ ，进一步写为： $\LARGE P(y|x;\theta)$ ，这也是很多博客在推导逻辑回归的极大似然函数所用到的写法。