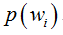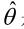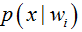前言：介绍了最简单的

问题

(这里都是玩具数据，为了方便理解才列出)

0123456789101112

X

1

2

3

4

4.2

4.4

4.6

4.8

5

6

7

8

y

0

0

0

0

1

1

1

1

0

0

0

0

假设 x = 4.9 用科学的办法估计 y 的分类。

预备知识

高斯分布的概率密度函数

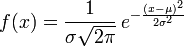
高斯分布的概率密度函数

理解

通常用「概率密度函数」代替概率，仅仅去比较大小。还有其他的分布，我也没有去深挖 :)。而不是直接求出概率。这非常重要！！！

求解问题

写出这个数据集的似然函数

还记得之前我们说过的「似然函数」吗？现在写出这个数据的「似然函数」

P(y=0 | x) = P(y=0 | x=1)P(y=0 | x=2)P(y=0 | x=3)P(y=0 | x=4)P(y=0 | x=5)P(y=0 | x=6)P(y=0 | x=7)P(y=0 | x=8)

P(y=1 | x) = P(y=1 | x=4.2)P(y=0 | x=4.4)P(y=0 | x=4.6)P(y=0 | x=4.8)

似然函数的本质描述出现这个情形的概率，最大化它即是是这个情形出现的概率最大。现在遇到了一个问题，我们无法写出等式左边的每一项。就更别谈最大化似然函数了。

常用的方法用概率密度函数替代概率。

比如：把 x = 1 带入概率密度函数代替 P(y=0 | x=1)。

所以最大化多个概率相乘变为了，最大化多个概率密度函数的相乘

最大化多个概率密度函数的相乘

取对数求导，并让导数为 0 。最后能得到一个非常舒适的结论。

最大化似然函数

解决问题

现在求得两组 (mu, sigma), (mu, sigma) 用来分别表示。

y = 1 时，最符合数据的概率密度函数 1

y = 0 时，最符合数据的概率密度函数 2

将 x = 4.9 分别带入函数 1、函数 2 中比较大小，最后确定 y 的类别。

最后总结

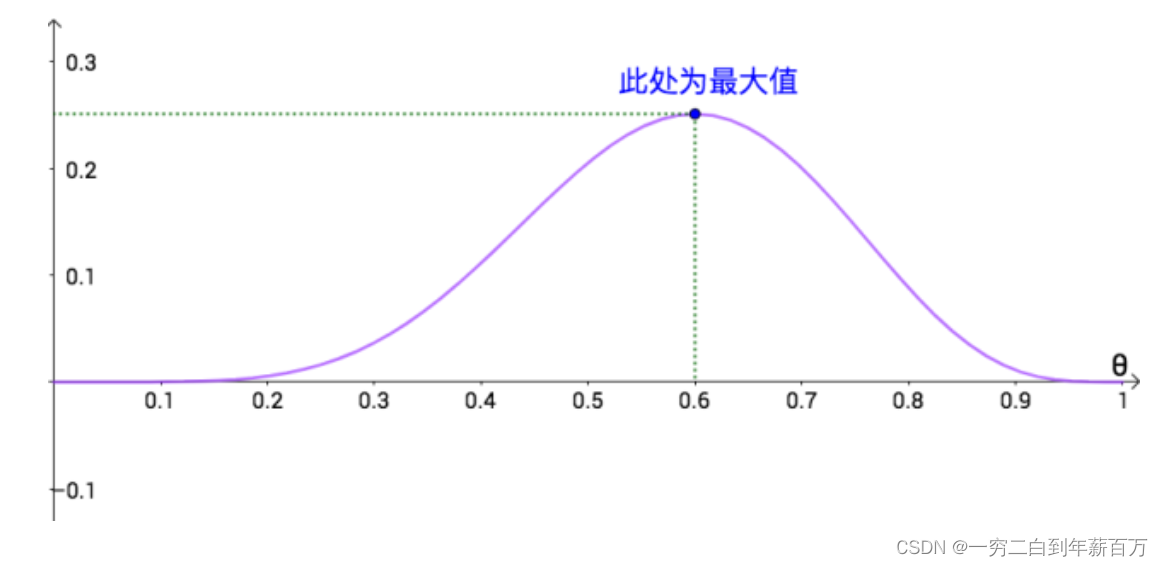
似然函数用来描述：已知情况的概率随参数变化的图像

最大化似然函数能得到，使这个情况出现概率最大的参数。

但是有时候，不能写出概率。常用概率密度函数代替概率。这非常重要。

如果假设高斯分布，那么通过「最大似然估计」会得到一个非常舒适的结果。见上述图片

最后结果的导出，使用概率密度函数来代替概率求解。