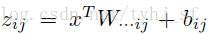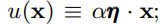激活函数总结

article/2025/9/27 6:52:14

一、引入激活函数的目的

在这里插入图片描述

图1：带一层隐藏层的神经网络

先看一个只含一层隐藏层的神经网络，如图1所示。输入为 n 条样本X，隐藏层H的权重和偏置分别为W_h，b_o，输出层O的权重和偏置分别为W_o，b_o。输出层的计算为：

H=XW_h+b_h (1)

O=HW_o+b_o (2)

将(1),(2)联合起来可得：

O=(XW_h+b_h)W_o+b_o=XW_hW_o+b_hW_o+b_o

从(3)可以看出，虽然加入了隐藏层，但是还是等效于单层的神经网络：权重为 W_hW_o ，偏置为 b_hW_o+b_o

上述的根本原因在于全连接只是对数据做仿射变换*，而多个仿射变换的叠加仍然是一个放射变换。因此有必要引入非线性变换，这个非线性变换就是今天要讲的激活函数。

*仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。简单来说，“仿射变换”就是：“线性变换”+“平移”

二、激活函数之性质

  1. **非线性：**即导数不是常数。保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。

  2. **可微性：**保证了在优化中梯度的可计算性。虽然 ReLU 存在有限个点处不可微，但处处 subgradient，可以替代梯度。

  3. **计算简单：**激活函数复杂就会降低计算速度，因此 RELU 要比 Exp 等操作的激活函数更受欢迎。

  4. 非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是 Sigmoid，它的导数在 x 为比较大的正值和比较小的负值时都会接近于 0。RELU 对于 x<0，其梯度恒为 0，这时候它也会出现饱和的现象。Leaky ReLU 和 PReLU 的提出正是为了解决这一问题。

  5. 单调性（monotonic）：即导数符号不变。当激活函数是单调的时候，单层网络能够保证是凸函数。但是激活函数如 mish 等并不满足单调的条件，因此单调性并不是硬性条件，因为神经网络本来就是非凸的。

  6. 参数少：大部分激活函数都是没有参数的。像 PReLU 带单个参数会略微增加网络的大小。还有一个例外是 Maxout，尽管本身没有参数，但在同样输出通道数下 k 路 Maxout 需要的输入通道数是其它函数的 k 倍，这意味着神经元数目也需要变为 k 倍。

三、sigmoid激活函数带来的梯度消失和爆炸问题

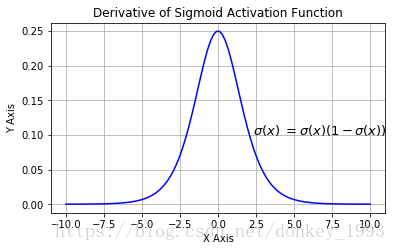
为了解决前面的问题，后来提出了sigmoid激活函数。sigmoid函数可以将元素的值变换到0和1之间，定义如下：

图2：sigmoid激活函数

def Sigmoid(x):return 1. / (1 + np.exp(-x))
#或
tf.nn.sigmoid(x,name=None)

sigmoid激活函数的导数为：
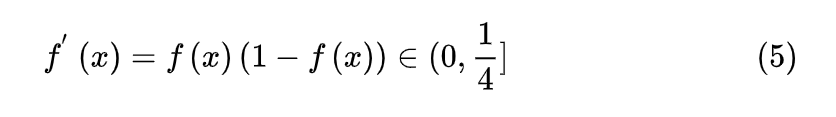
在这里插入图片描述
优点：

  • 梯度平滑，求导容易
  • Sigmoid函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用作输出层

缺点：

  • 激活函数计算量大（在正向传播和反向传播中都包含幂运算和除法）；
  • 梯度消失：输入值较大或较小（图像两侧）时，sigmoid导数则接近于零，因此在反向传播时，这个局部梯度会与整个代价函数关于该单元输出的梯度相乘，结果也会接近为 0 ，无法实现更新参数的目的；
  • Sigmoid 的输出不是 0 为中心（zero-centered）。因为如果输入都是正数的话
    在这里插入图片描述
    在这里插入图片描述

sigmoid激活函数虽然增强了模型的非线性表达能力，但是却带来了梯度消失和爆炸的问题，下面具体分析下是如何导致的。

3.1sigmoid可能带来的梯度消失

在这里插入图片描述
在这里插入图片描述
从公式(10)可以看出，随着反向传播链式求导，层数越多最后的梯度越小，最终导致梯度消失。

3.2 sigmoid可能带来的梯度爆炸

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
图4显示了公式(13)中的 x 数值范围随 w 的变化，可以看到 x 的最大数值范围也仅仅为0.45，因此仅仅在很窄的范围内才可能出现梯度爆炸。

根据3.1和3.2节，可以得出以下结论：

  • sigmoid激活函数在深层神经网络中极大概率会引起梯度消失
  • sigmoid激活函数很小的概率会出现梯度爆炸

由于sigmoid的局限性，所以后来很多人又提出了一些改进的激活函数，比如：ReLU，Leaky-ReLU，PReLU，Dice，RReLU等。后面具体介绍下几个激活函数的区别。

四、常用激活函数对比

（一）饱和

4.1sigmoid激活函数

4.2Tanh激活函数

在这里插入图片描述

tf.nn.tanh(x,name=None)

优点：

比Sigmoid函数收敛速度更快
tanh(x) 的梯度消失问题比 sigmoid 要轻
相比Sigmoid函数，输出是以 0 为中心 zero-centered
缺点：

还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。

（二）饱和

在这里插入图片描述

def tanh(x):return np.sinh(x)/np.cosh(x)

优点：

  • 比Sigmoid函数收敛速度更快
  • tanh(x) 的梯度消失问题比 sigmoid 要轻
  • 相比Sigmoid函数，输出是以 0 为中心zero-centered

缺点：

  • 还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。

4.3 ReLU（整流线性单元）

ReLU是Krizhevsky、Hinton等人在2012年《ImageNet Classification with Deep Convolutional Neural Networks》论文中提出的一种激活函数，可以用来解决梯度消失的问题，其定义如下：
在这里插入图片描述
从公式(14)可以看出ReLU在正区间的导数为1，因此不会发生梯度消失。关于ReLU的缺点，可以参见下面的描述：

神经网络在训练的时候，一旦学习率没有设置好，第一次更新权重的时候，输入是负值，那么这个含有ReLU的神经节点就会死亡，再也不会被激活。因为：ReLU的导数在
x>0 的时候是1，在 x<= 0 的时候是0。如果 x<= 0
，那么ReLU的输出是0，那么反向传播中梯度也是0，权重就不会被更新，导致神经元不再学习。
在实际训练中，如果学习率设置的太高，可能会发现网络中40%的神经元都会死掉，且在整个训练集中这些神经元都不会被激活。所以，设置一个合适的较小的学习率，会降低这种情况的发生。为了解决神经元节点死亡的情况，有人提出了Leaky-ReLU，PReLu，RReLU，ELU等激活函数。

总结一下ReLU的优缺点。

优点：

  • ReLU解决了梯度消失的问题，因为导数为 1，不会像 sigmoid 那样由于导数较小，而导致连乘得到的梯度逐渐消失。更加有效率的梯度下降以及反向传播
  • 由于ReLU线性特点，神经网络的计算和训练比sigmoid快很多，计算与收敛速度非常快：不涉及指数等运算
  • 会使一部分神经元输出为0，造成网络的稀疏性，减少参数间的依存关系，缓解过拟合

缺点：

  • ReLU可能会导致神经元死亡，权重无法更新。【某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。】
  • 当输入是负数的时候，ReLU 是完全不被激活的，这就表明一旦输入到了负数，ReLU 就会死掉。这样在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，这个和 sigmod 函数、tanh 函数有一样的问题。
  • 我们发现 ReLU 函数的输出要么是0，要么是正数，这也就是说，ReLU 函数也不是以0为中心的函数。

尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

 def ReLU(x):return x * (x > 0)

tf.nn.relu(features, name=None)

ARGS：

features：A
Tensor。必须是下列类型之一：float32，float64，int32，uint8，int16，int8，int64，bfloat16，uint16，half，uint32，uint64，qint8。
name：操作的名称(可选)。 Returns:

一个Tensor，与features具有相同的类型。

4.4指数线性单元(ELU)

在这里插入图片描述
x<0时，f(x)=a(exp(x)-1)

优点：

  • 能避免死亡 ReLU 问题：x 小于 0 时函数值不再是 0，因此可以避免 dying relu 问题；
  • 能得到负值输出，这能帮助网络向正确的方向推动权重和偏置变化。

缺点：

  • 计算耗时：包含指数运算；
  • α 值是超参数，需要人工设定

4.4 Leaky-ReLU

Leaky-ReLU是Andrew L. Maas等人在2013年《Rectifier Nonlinearities Improve Neural Network Acoustic Models（Leaky ReLU）》论文中提出的一种激活函数。**由于ReLU将所有负数部分的值设为0，从而造成神经元的死亡。而Leaky-ReLU是对负值给与一个非零的斜率，从而避免神经元死亡的情况。**Leaky-ReLU定义如下：
在这里插入图片描述
Leaky-ReLU很好的解决了ReLU中神经元死亡的问题。因为Leaky-ReLU保留了 x<0 时的梯度，在 x<0 时，不会出现神经元死亡的问题。总结一下Leaky-ReLU的优缺点。

优点：

  • Leaky-ReLU解决了ReLU中神经元死亡的问题
  • 由于Leaky-ReLU线性特点，神经网络的计算和训练比sigmoid快很多

缺点：

  • Leaky-ReLU中的超参 alpha 需要人工调整
tf.nn.maximum(x,leaky*x,name=None)#leaky为超参

4.5 PReLU(Parametric Rectified Linear Unit)，顾名思义：带参数的ReLU

PReLU是Kaiming He等人在2015年《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》论文中提出的激活函数。和Leaky-ReLU相比，将 α 变成可训练的参数，不再依赖于人工调整。PReLU的定义如下：
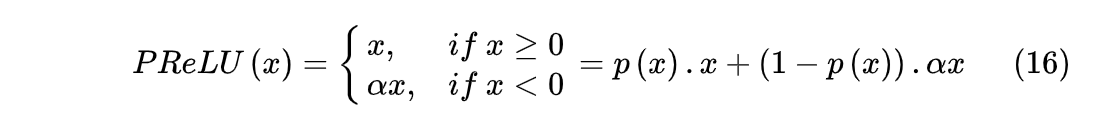
在这里插入图片描述

在这里插入图片描述
其中 alpha 是可训练的参数。
PReLU的几点说明
（1） PReLU只增加了极少量的参数，也就意味着网络的计算量以及过拟合的危险性都只增加了一点点。特别的，当不同channels使用相同的ai时，参数就更少了。

（2） BP更新ai时，采用的是带动量的更新方式，如下图：
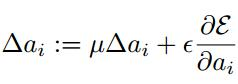
在这里插入图片描述
上式的两个系数分别是动量和学习率。
**需要特别注意的是：**更新ai时不施加权重衰减(L2正则化)，因为这会把ai很大程度上push到0。事实上，即使不加正则化，试验中ai也很少有超过1的。

（3） 整个论文，ai被初始化为0.25。
TensorFlow学习笔记之 PReLU激活函数原理和代码中的代码与上文论文中的公式不同，仅用于他的模型是可以的，不会过拟合
但出现OOM报错，空间复杂度还是太高了，因此要慎用
优点：

  • 与 ReLU 相同。

缺点：

  • 在不同问题中，表现不一。

4.6 Dice

Dice是Guorui Zhou等人在2018年《Deep Interest Network for Click-Through Rate Prediction》论文中提出的激活函数。根据 Parametric ReLU 改造而来，ReLU类函数的阶跃变化点再x=0处，意味着面对不同的输入这个变化点是不变的，DIN中改进了这个控制函数，让它根据数据的分布来调整，选择了统计神经元输出的均值和方差(实际上就是Batch_Normalization,CTR中BN操作可是很耗时的，可以推测Dice复杂的计算快不起来不会大规模引用)来描述数据的分布。Dice是对PRelu做了平滑，使得拐点不再是固定的0，而是依赖于数据的分布，定义如下：
在这里插入图片描述
深度学习中Batch Normalization和Dice激活函数中提到DICE是BN的一种变换（有具体公式），是解决internal coviriate shift问题的一种方法 ，并提到实际解决问题时要注意BN在训练时和测试时都要启动
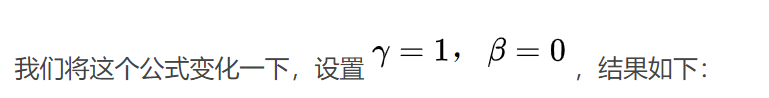
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

优点：

  • 根据数据分布灵活调整阶跃变化点，具有BN的优点(解决Internal Covariate
    Shift)，原论文称效果好于Parametric ReLU。

缺点：

  • 具有BN的缺点，大大加大了计算复杂度。

4.7 RReLU

RReLU(Randomized Leaky ReLU)的首次提出是在Kaggle比赛NDSB中，也是Leaky-ReLU的一个变体。RReLU在训练的过程中，α是从均匀分布 U( u,l ) 中随机选取的，RReLU在训练过程中的定义如下：
在这里插入图片描述
在这里插入图片描述

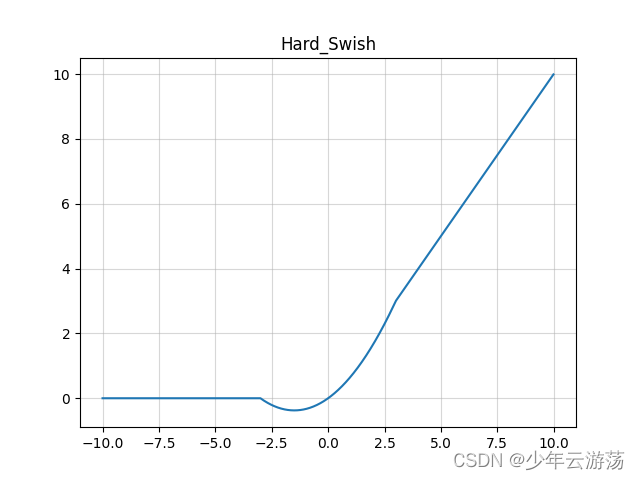
4.8Swish

在这里插入图片描述
在使用了BN算法情况下，β需要被调节，变为可调节参数，而非固定值

Swish 在深层模型上的效果优于 ReLU。例如，仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%，Inception-ResNet-v 的分类准确率提高 0.6%。
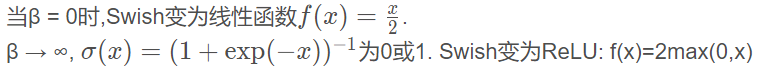
在这里插入图片描述

所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数.

def Swish(x,beta=1):return x*tf.nn.sigmoid(beta*x)

4.9SELU

在这里插入图片描述
在这里插入图片描述
优点：

  • SELU 激活能够对神经网络进行自归一化（self-normalizing）；
  • 不可能出现梯度消失或爆炸问题，论文附录的定理 2 和 3 提供了证明。

缺点：

  • 应用较少，需要更多验证；
  • lecun_normal 和 Alpha Dropout：需要 lecun_normal 进行权重初始化；如果 dropout，则必须用
    Alpha Dropout 的特殊版本。

(三)softmax和maxout

4.10 softmax 多分类

Sigmoid函数只能处理两个类别，这不适用于多分类的问题，所以Softmax可以有效解决这个问题。Softmax函数很多情况都运用在神经网路中的最后一层网络中，使得每一个类别的概率值在(0, 1)之间。
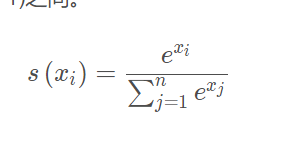
在这里插入图片描述

def softmax(x):
return np.exp(x) / sum(np.exp(x))

4.11 maxout（不能算作传统意义的激活函数，是一种网络选择器）

可以理解为单个神经元的扩展,主要是扩展单个神经元里面的激活函数, 将激活函数变成一个网络选择器,原理就是将多个神经元并列地放在一起，从他们的输出结果中找到最大的那个,代表对特征响应最敏感,然后取这个神经元的结果参与后面的运算
在这里插入图片描述

优点：

  • Maxout 神经元拥有 ReLU 单元的所有优点（线性和不饱和），而没有它的缺点（死亡的 ReLU 单元）

缺点：

  • 和 ReLU 对比，它每个神经元的参数数量增加了一倍，这就导致整体参数的数量激增。

五、总结

从最初的sigmoid到后面的Leaky ReLU、PReLU，再到近期的SELUs、GELUs，激活函数的改进从来没有中断过。激活函数不仅解决了深层神经网络的梯度消失和爆炸问题，同时对于模型的拟合能力和收敛速度起着至关重要的重用。因此了解激活函数的相关原理还是非常有必要的。
参考：
深度学习中激活函数总结
深度学习——PReLU激活
整理Sigmoid~Dice常见激活函数，从原理到实现


http://chatgpt.dhexx.cn/article/wMn3Wd9W.shtml

相关文章

机器学习（14）——激活函数

机器学习（14）——激活函数

文章目录 1 定义2 激活函数的必要性3 常用的激活函数3.1 单位阶跃函数3.2 Logistic函数3.3 Tanh函数3.4 ReLU函数3.5 LeakyReLU函数3.6 Softmax函数 4 选择恰当的激活函数 1 定义 激活函数 (Activation functions) 对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说…
阅读更多...
GELU激活函数

GELU激活函数

最近看bert论文&#xff0c;发现用的是GELU激活函数&#xff0c;找出来看看 论文&#xff1a;GAUSSIAN ERROR LINEAR UNITS (GELUS)项目&#xff1a;https://github.com/hendrycks/GELUs ABSTRACT 本文提出了高斯误差线性单元(GELU)&#xff0c;一个高性能的神经网络激活函数…
阅读更多...
神经网络中的激活函数

神经网络中的激活函数

文章目录 引言什么是激活函数&#xff1f;为什么我们要在神经网络中使用激活函数&#xff1f;线性激活函数非线性激活函数1. Sigmoid&#xff08;逻辑激活函数&#xff09;2. Tanh&#xff08;双曲正切激活函数&#xff09;3. ReLU&#xff08;线性整流单元&#xff09;激活函数…
阅读更多...
激活函数简述

激活函数简述

1、激活函数的作用 1.不带激活函数的单层感知机是一个线性分类器&#xff0c;不能解决线性不可分的问题 2.合并后的多个感知器本质上还是一个线性分类器&#xff0c;还是解决不了非线性的问题 3.激活函数是用来加入非线性因素的&#xff0c;提高神经网络对模型的表达能力&a…
阅读更多...
常用激活函数

常用激活函数

文章目录 前言为什么需要激活函数什么样的函数可以做激活函数什么样的函数是好的激活函数常用激活函数sigmoidtanhReLULeaky ReLURandomized Leaky ReLUMaxout 参考文章 前言 今天这篇文章对一些常用激活函数做一下总结吧。在神经网络中激活函数还是很重要的&#xff0c;并且熟…
阅读更多...
激活函数

激活函数

深度学习中的激活函数导引 我爱机器学习(52ml.net) 2016年8月29日 0 作者&#xff1a;程程 链接&#xff1a;https://zhuanlan.zhihu.com/p/22142013 来源&#xff1a;知乎 著作权归作者所有&#xff0c;已联系作者获得转载许可。 深度学习大讲堂致力于推送人工智能&#xff0c…
阅读更多...
详解激活函数

详解激活函数

文章目录 0️⃣前言1️⃣Sigmoid2️⃣tanh3️⃣Relu4️⃣Leaky Relu5️⃣Softmax6️⃣总结 0️⃣前言 用了这么久的激活函数&#xff0c;抽空总结一下吧&#xff0c;不然总是忘记&#xff0c;这里介绍常用到的sigmoid&#xff0c;tanh&#xff0c;relu&#xff0c;leaky relu&…
阅读更多...
常用激活函数（激励函数）理解与总结

常用激活函数（激励函数）理解与总结

引言 学习神经网络的时候我们总是听到激活函数这个词&#xff0c;而且很多资料都会提到常用的激活函数&#xff0c;比如Sigmoid函数、tanh函数、Relu函数。那么我们就来详细了解下激活函数方方面面的知识。本文的内容包括几个部分&#xff1a; 什么是激活函数&#xff1f;激活…
阅读更多...
常用激活函数总结（深度学习）

常用激活函数总结（深度学习）

前言   学习神经网络的时候我们总是听到激活函数这个词&#xff0c;而且很多资料都会提到常用的激活函数&#xff0c;比如Sigmoid函数、tanh函数、Relu函数。在经过一段时间学习后&#xff0c;决定记录个人学习笔记。 一、激活函数 1.激活函数定义&#xff1f;   在神经网…
阅读更多...
【概念梳理】激活函数

【概念梳理】激活函数

一、引言 常用的激活函数如下&#xff1a; 1、Sigmoid函数 2、Tanh函数 3、ReLU函数 4、ELU函数 5、PReLU函数 6、Leaky ReLU函数 7、Maxout函数 8、Mish函数 二、激活函数的定义 多层神经网络中&#xff0c;上层节点的输出和下层节点的输入之间具有一个函数关系&#xff0c;…
阅读更多...
一文搞懂激活函数

一文搞懂激活函数

目录 1、什么是激活函数 2、激活函数的用途&#xff08;为什么需要激活函数&#xff09;&#xff1f; 3、常见的激活函数介绍 3.1 Sigmoid函数 3.2 tanh函数 3.3.RelU函数 3.4 Leaky ReLU函数 和 PReLU 函数 --- ReLU 变体的提出 3.5 ELU (Exponential Linear Units) 函…
阅读更多...
激活函数（Relu，sigmoid，Tanh，softmax）详解

激活函数（Relu，sigmoid，Tanh，softmax）详解

目录 1 激活函数的定义 2 激活函数在深度学习中的作用 3 选取合适的激活函数对于神经网络有什么样的重要意义 4 常用激活函数 4.1 Relu 激活函数 4.2 sigmoid 激活函数 4.3 Tanh激活函数 4.4 softmax 激活函数 1 激活函数的定义 激活函数&#xff08;Activation Funct…
阅读更多...
激活函数（Activation Function）

激活函数（Activation Function）

目录 1 激活函数的概念和作用 1.1 激活函数的概念 1.2 激活函数的作用 1.3 通俗的理解一下激活函数(图文结合) 1.3.1 无激活函数的神经网络 1.3.2 带激活函数的神经网络 2 神经网络梯度消失与梯度爆炸 2.1 简介梯度消失与梯度爆炸 2.2 梯度不稳定问题 2.3 产生梯度消…
阅读更多...
常用的激活函数合集（详细版）

常用的激活函数合集（详细版）

目录 一、定义以及作用 二、常用激活函数解析 1、Sigmoid函数 1.1 公式 1.2 对应的图像 1.3 优点与不足之处 1.4 对应pytorch的代码 2、Tanh函数 2.1 公式 2.2 对应的图像 2.3 优点与不足之处 2.4 对应pytorch的代码 3、ReLU 3.1 公式 3.2 对应的图像 3.3 优点与不…
阅读更多...
优化算法——FTRL

优化算法——FTRL

ctr预测中&#xff0c;单个样本由向量x表示&#xff0c;w是模型参数&#xff0c;预测样本x被点击的概率psigmoid(w * x)&#xff0c;sigmoid(x) 1/(1exp(x))。样本label为{0, 1}表示是否被点击。模型损失函数为交叉熵损失&#xff1a; L -ylog - (1-y)log(1-p)&#xff0c;梯…
阅读更多...
【深度学习】优化算法-Ftrl

【深度学习】优化算法-Ftrl

脑图 代码实现 DO WHAT THE FUCK YOU WANT TO PUBLIC LICENSEVersion 2, December 2004Copyright (C) 2004 Sam Hocevar <samhocevar.net>Everyone is permitted to copy and distribute verbatim or modified copies of this license document, and changing it is all…
阅读更多...
谷歌13年提出来的类似于lr的算法 - ftrl论文翻译（七）

谷歌13年提出来的类似于lr的算法 - ftrl论文翻译（七）

论文链接&#xff1a;https://static.googleusercontent.com/media/research.google.com/zh-CN//pubs/archive/41159.pdf 概要 预测广告点击率&#xff08;CTR&#xff09;是一个巨大的规模学习问题&#xff0c;是在线广告业数十亿美元的核心问题。 我们从最近的实验中选择出…
阅读更多...
FTRL 算法

FTRL 算法

本文会尝试总结FTRL的发展由来&#xff0c;总结从LR -> SGD -> TG -> FOBOS -> RDA -> FTRL 的发展历程。本文的主要目录如下&#xff1a; 一、 反思魏则西事件。 二、 LR模型 三、 SGD算法 四、 TG算法 五、 FOBOS算法 六、 RDA算法 七、 FTRL算法 注&…
阅读更多...
排序模型进阶-FMFTRL

排序模型进阶-FMFTRL

日萌社 人工智能AI&#xff1a;Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战&#xff08;不定时更新&#xff09; 5.8 排序模型进阶-FM&FTRL 学习目标 目标 无应用 无 5.8.1 问题 在实际项目的时候&#xff0c;经常会遇到训练数据非常大导致一些算法实际…
阅读更多...
以我视角深入理解FTRL模型原理

以我视角深入理解FTRL模型原理

以我视角深入理解FTRL模型原理 FTRL算法是吸取了FOBOS算法和RDA算法的优点而衍生而来的算法。 1.FOBOS算法 小结&#xff1a; 2. RDA算法 RDA也叫正则对偶平均算法&#xff0c;特征权重更新如下&#xff1a; 小结&#xff1a; 3.FTRL算法原理 从loss function的形式来看&am…
阅读更多...
推荐文章

Copyright @ 2022~2023