无向图邻接表实现
顶点:按照编号顺序将顶点数据存储在一维数组当中
关联同一个顶点的边(以顶点为尾的弧):用线性链表存储
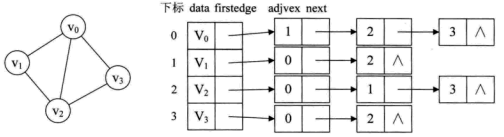
头结点:data+firstarc
表结点:adjvex(邻接点的序号,存放与vi邻接的顶点在表头数组中的位置)+nextarc(指向下一个边/弧的指针)

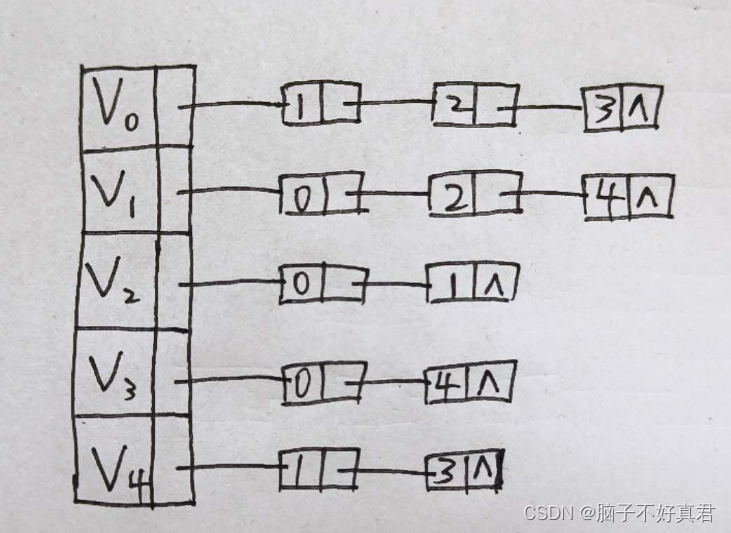
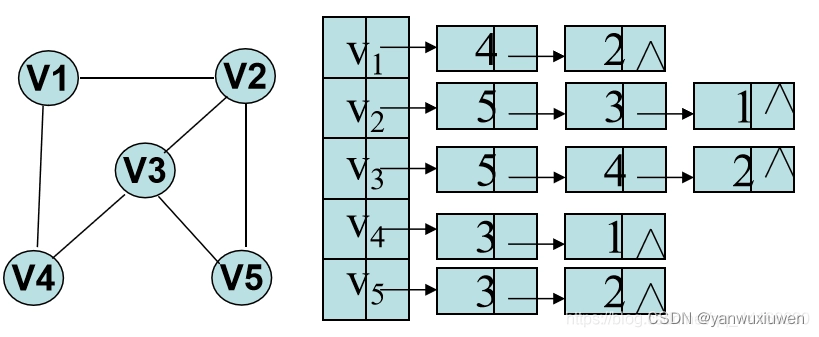
无向图的邻接表
特点:
-
邻接表不唯一
-
若无向图中有n个顶点、e条边,则其邻接表需要n个头结点和2e个表结点。适合存储稀疏图
即空间复杂度为 O(n+2e)
-
有几个表结点就是有几个与其头结点相关联的边,也就是它的度是多少
-
无向图中顶点vi的度为第i个单链表中的结点数
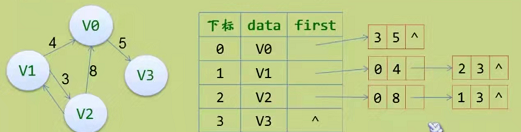
有向图的邻接表
表结点:adjvex(头结点i为弧尾>的弧的结点)+nextarc(指向下一个边/弧的指针)
特点:
-
若有向图中有n个顶点、e条边,则其邻接表需要n个头结点和e个表结点,即空间复杂度为O(n+e)
-
顶点vi的出度为第i个单链表中的结点个数
-
顶点vi的入度为整个单链表中邻接点阈值是i-1的结点的个数
找出度容易,找入度难
使用逆邻接表:表结点:adjvex(头结点i为弧头的弧的结点)+nextarc(指向下一个边/弧的指针)
这种邻接表找入度容易找出度难
当邻接表的存储结构形成后,图便唯一确定

AdjList[MVNum]是VNode结点构成的数组类型
即定义AdjList v相当于VNode v[MVNum]
边结点的定义:

图的结构的定义:

算法思想:
- 输入总顶点数和总边数
- 建立顶点表
- 依次输入各个点的信息存入顶点表中
- 使每个表头结点的指针域都初始化为NULL
- 创建邻接表
- 依次输入每条边依附的两个顶点
- 查找确定两个顶点的序号i和j,建立边结点
- 将此边结点分别插入到vi和vj对应的两个边链表的头部,利用头插法,每次都插入在表结点的后面


代码实现创建邻接表
#include<iostream>
using namespace std;
#define OK 1
#define ERROR 0
#define FALSE 0
#define TRUE 1
#define MAXNum 100
//定义无穷大
#define MAXInt 32767
typedef int Status;
//定义顶点数据类型
typedef char VerTexType;
//定义节点权重的类型
typedef int OtherInfo;
//定义边的数据类型
typedef struct ArcNode {int adjvex;//该边指向的顶点的位置ArcNode* nextarc;//指向下一条边的指针OtherInfo info;//与边相关的信息
}ArcNode;
//定义表结点的类型
typedef struct VNode {VerTexType data;//顶点信息ArcNode* firstarc;//指向第一条依附该顶点的边的指针
}VNode,AdjList[MAXNum];//AdjList是邻接表类型
//图结构的类型
typedef struct {AdjList vertices;//邻接表int vexnum, arcnum;//图当前顶点数和弧数
}ALGraph;//图的定义
//该函数查找顶点x在图的顶点表中的下标
int LocateVex(ALGraph G, VerTexType x) {for (int i = 0; i < G.vexnum; i++) {if (G.vertices[i].data == x) {return i;}}return -1;
}//邻接表的创建——无向图
Status createUDN(ALGraph &G) {cout << "请输入无向图的总结点的数目和总的边数" << "\n";cin >> G.vexnum >> G.arcnum;cout << "请输入无向图中的各个顶点" << "\n";for (int i = 0; i < G.vexnum; i++){cin>>G.vertices[i].data;//初始化表头结点的指针域G.vertices[i].firstarc = NULL;}cout << "请输入每条边的信息:(顶点1 顶点2)" << "\n";for (int i = 0; i < G.arcnum; i++) {VerTexType x, y;cin >> x >> y;//查找两个顶点的下标int xIndex=LocateVex(G, x);int yIndex=LocateVex(G, y);//找到这两个顶点的下标之后就可以往firstarc域插入表结点了ArcNode* xArcNode = new ArcNode;ArcNode* yArcNode = new ArcNode;if (xIndex != -1 && yIndex != -1) {//在x结点后面插入邻接y结点的信息xArcNode->info = 1;xArcNode->adjvex = yIndex;xArcNode->nextarc = G.vertices[xIndex].firstarc;G.vertices[xIndex].firstarc = xArcNode;//在y结点后面插入邻接x结点的信息yArcNode->info = 1;yArcNode->adjvex = xIndex;yArcNode->nextarc = G.vertices[yIndex].firstarc;G.vertices[yIndex].firstarc = yArcNode;}else{return ERROR;}}return OK;
}void outPut(ALGraph G) {cout << "输出顶点表如下:" << "\n";for (int i = 0; i < G.vexnum; i++){cout << G.vertices[i].data << " ";}cout << "\n输入邻接表如下:" << "\n";for (int i = 0; i < G.vexnum; i++){printf("%c顶点相邻接的顶点为:\n", G.vertices[i].data);ArcNode* p=G.vertices[i].firstarc;while (p) {printf("%c ", G.vertices[p->adjvex].data);p = p->nextarc;}printf("\n");}}int main() {ALGraph G;createUDN(G);//输出该图进行查看,是否正确outPut(G);return 0;
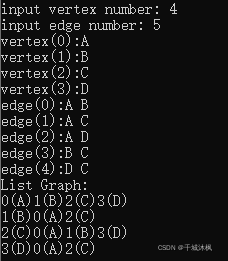
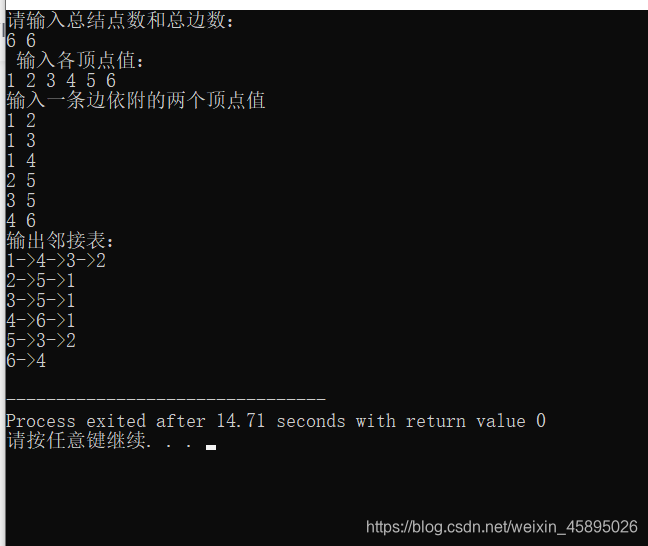
}测试样例:


邻接表示法的优缺点以及和邻接矩阵的关系
优缺点:
- 方便找任一顶点的所有“邻接点”
- 节约稀疏图的空间
- 需要N个头指针和2E个结点(每个结点至少两个域)
- 方便计算任一顶点的“度”
- 对无向图来说:是的
- 对有向图:只能计算“出度”;需要构造逆邻接表(存指向自己的边)来方便计算“入度”
- 不方便检查任意一对顶点之间是否存在边
联系
- 邻接表中每个链表对应于邻接矩阵的一行,链表中结点个数等于一行中非零元素的个数
区别
- 对任一确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但是邻接表是不唯一的(链接次序与顶点编号无关)
- 邻接矩阵空间复杂度为O(n2),而邻接表的空间复杂度为O(n+e)
- 邻接矩阵多用于稠密图,而邻接表多用于稀疏图