呃，下面该写邻接表了.......

邻接表的出现是因为图若是稀疏图，用邻接矩阵会造成空间的浪费，毕竟你要开辟一个一维数组和一个二维数组嘛，而且还是大开小用的那种。

邻接表为了避免内存的浪费引入了链式存储，它的处理办法是：

1.用一个一维数组存储顶点，当然你也可以用单链表存储，

2.用单链表存储顶点的邻接点，可以将顶点改为结构体数组，结构体中存放邻接点的指针，邻接点也创建一个结构体，定义指针next存放该顶点的另一个邻接点，这样就可以把该顶点的所有邻接点串起来了。

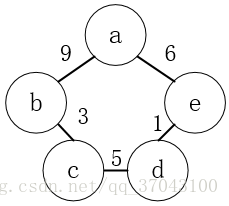
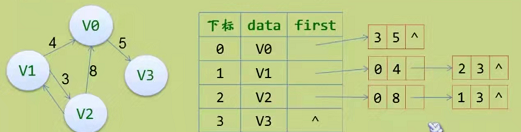
下面是一个无向的网图：

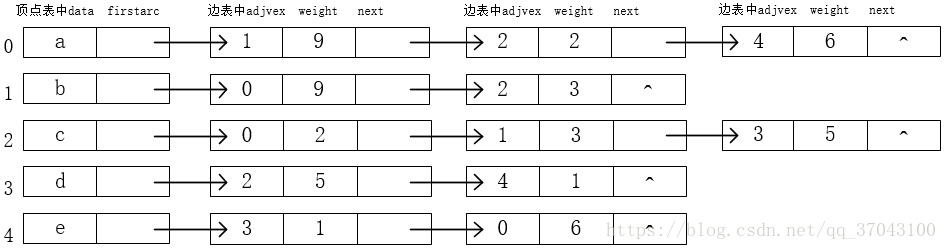
邻接表中数据的存储图示如下（emmm，无向图果然没有有向图好画）：

emmm，终于画完了，我来介绍下这个图

顶点表也就是个结构体数组，是存放顶点的结构，顶点表中有data元素，存放顶点信息  firstarc是一个边结构体表指针，存放邻接点的信息。

边表也是一个结构体，内有adivex元素，存放邻接点的下标，weight存放顶点与邻接点之间线的权重，next是边表结构体指针，存放该顶点的下一个邻接点，next就是负责将顶点的邻接点连起来。

看着上面的图慢慢理解吧！

下面则是代码部分：

#include <iostream>
using namespace std;#define MAXVERTEX 100   //最大顶点数
typedef char vertextype;    //定义顶点的存储类型
typedef int arctype;    //定义边的权值类型typedef struct ArcNode  //边表节点
{int adjvex; //邻接点域，存储该顶点对应的下标arctype wigth;  //用于存储权值struct ArcNode *next; //链域，指向下一个邻接点
}ArcNode;typedef struct VertexNode   //顶点表节点
{vertextype data;    //存储顶点数据的信息ArcNode *firstarc;  //边表头指针
}VertexNode, AdjList[MAXVERTEX];typedef struct
{AdjList adjlist;    //定义邻接表int numvertex;  //当前邻接表的顶点数int numarc; //当前邻接表的边数
}GraphAdjList;//建立图的邻接表
void CreateAdjListGraph(GraphAdjList &G)
{ArcNode *e;cin >> G.numvertex; //输入当前图的顶点数cin >> G.numarc;    //输入当前图的边数for(int i = 0; i < G.numvertex; i++)    //建立顶点表{cin >> G.adjlist[i].data;   //输入顶点信息G.adjlist[i].firstarc = NULL;   //将表边指针置为空}for(int k = 0; k < G.numarc; k++){int i, j, w;cin >> i >> j >> w; //输入边两边的顶点和边上的权重e = new ArcNode;   //创建一个表边节点指针e->adjvex = j;e->wigth = w;e->next = G.adjlist[i].firstarc;G.adjlist[i].firstarc = e;//因为是无向图，彼此相对称e = new ArcNode;   //创建一个表边节点指针e->adjvex = i;e->wigth = w;e->next = G.adjlist[j].firstarc;G.adjlist[j].firstarc = e;}
}//打印邻接表
void PrintfGraphAdjList(GraphAdjList G)
{for(int i = 0; i < G.numvertex; i++){ArcNode *p = G.adjlist[i].firstarc;cout << G.adjlist[i].data << '\t';while(p){cout << p->adjvex << ' ' << p->wigth << '\t';p = p->next;}cout << endl;}
}
int main()
{GraphAdjList G;CreateAdjListGraph(G);PrintfGraphAdjList(G);return 0;
}

邻接表的时间复杂度：n为顶点数，e为边数 O（n + e）……

 

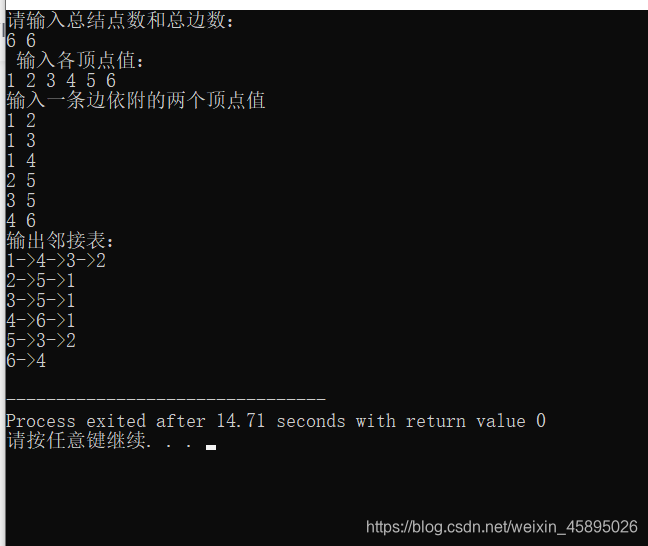
运行结果（根据上图的信息输入）：