一、邻接表表示法

回忆在线性表时，顺序存储结构就存在预先分配内存可能造成存储空间浪费的问题，于是引出了链式存储结构，同样的，我们可以考虑对边或弧使用链式存储方式来避免空间浪费问题

邻接表是图的一种链式存储结构。

由两部分组成：表头结点表和边表。

邻接表中每个单链表的第一个结点存放有关顶点的信息，把这一结点看成链表的表头，其余结点存放有关边的信息

（1）表头结点表：包括数据域和链域，数据域存储顶点的名称，链域用于指向链表中第一个结点（与顶点邻接的第一个顶点）

（2）边表：包括邻接点域（指示与顶点邻接的点在图中的位置，即数组下标）、数据域（存储和边相关的信息，如权值）、链域（指示与顶点邻接的下一条边的结点）。

表头结点表：
在这里插入图片描述
边表：

无向图的邻接表

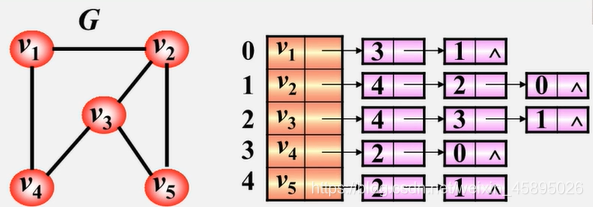
在这里插入图片描述

特点：

邻接表不唯一（边表顺序可以互换）
若无向图中有n个顶点、e条边，则其邻接表需n个头结点和2e个边结点，复杂度为O（n+2e）<O(n^2),所以适合存储稀疏图
无向图中顶点Vi的度为第i个单链表中的结点数。

有向图的邻接表

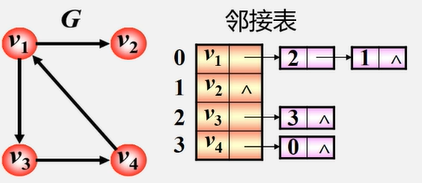
在这里插入图片描述
特点：

顶点vi的出度为第i个单链表中的结点个数
顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数(需要遍历整个整个邻接表，较麻烦)。

为了便于确定顶点的入度，可以建立一个有向图的逆邻接表，即对每个顶点vi建立一个链接所以进入vi的边的表

有向图的逆邻接表

与上图同步

在这里插入图片描述
特点：

顶点vi的入度为第i个单链表中的结点个数
顶点vi的出度为整个单链表中邻接点域值是i-1的结点个数

此时我们很容易就可以算出某个顶点的入度或出度是多少，判断两顶点是否存在弧也很容易实现。

二、图的邻接表存储表示

//边的结点结构
#define MVNum 100 //最大顶点数
typedef struct ArcNode{int adjvex;  //该边所指向的顶点的位置 struct ArcNode *nextarc;//指向下一条边的指针 Otherinfo info;  //和边相关的信息 
}ArcNode;//顶点的结点结构 
typedef struct VNode{VerTexType data;//顶点信息、ArcNode *firstarc;//指向第一条依附该顶点的边的指针 
}VNode,AdjList[MVNum];//AdjList表示邻接表类型//图的结构定义 
typedef struct{AdjList vertices; //定义一个数组vertices,是vertex的复数形式int vexnum,arcnum; //图的当前顶点数和弧数
}ALGraph;

三、采用邻接表表示法创建无向网

//创建无向图G 
bool CreateUDG(ALGraph &G){ int i,j,k,v1,v2;cin>>G.vexnum>>G.arcnum;//输入总顶点数，总边数for(i=0;i<G.vexnum;i++){//输入各顶点，构造表头结点表 cin>>G.vertices[i].data;//输入顶点值 G.vertices[i].firstarc=NULL;//初始化表头结点的指针域}//for//输入各边，构造邻接表for(k=0;k<G.arcnum;k++){cin>>v1>>v2;    //输入一条边依附的两个顶点 i=LocateVex(G,v1);j=LocateVex(G,v2); //确定顶点在G.vertices中的序号ArcNode *p1=new ArcNode;  //生成一个新的边结点*p1p1->adjvex=j;  //邻接点序号为j //头插法将新结点*p1插入顶点vi的边表头部 p1->nextarc=G.vertices[i].firstarc;G.vertices[i].firstarc=p1; ArcNode *p2=new ArcNode;p2->adjvex=i;  //邻接点序号为i//头插法插入p2 ,因为是无向网，所以是两条 p2->nextarc=G.vertices[i].firstarc;G.vertices[i].firstarc=p2; }//forreturn true; 
}//CreateUDG

算法时间复杂度是O(n+e)；

int LocateVex(ALGraph G,VerTexType u){//在图G中查找顶点u，存在则返回顶点表中的下标；否则返回-1int i;for(i=0;i<G.vexnum;i++)if(u==G.vertices[i])return i;return -1;
}

注意：一个图的邻接矩阵表示是唯一的，但其邻接表表示不唯一，这是因为邻接表表示中，各边表结点的链接次序取决于建立邻接表的算法，以及边的输入次序

代码实现此邻接表：

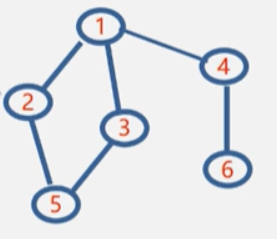
在这里插入图片描述

#include<iostream>
#include<queue>
using namespace std; 
#define MVNum 100 //最大顶点数typedef struct ArcNode{int adjvex;  //该边所指向的顶点的位置 struct ArcNode *nextarc;//指向下一条边的指针 
}ArcNode;//顶点的结点结构 
typedef struct VNode{char data;//顶点信息、ArcNode *firstarc;//指向第一条依附该顶点的边的指针 
}VNode,AdjList[MVNum];//AdjList表示邻接表类型//图的结构定义 
typedef struct{AdjList vertices; //定义一个数组vertices,是vertex的复数形式int vexnum,arcnum; //图的当前顶点数和弧数
}ALGraph;int LocateVex(ALGraph G,int u){//在图G中查找顶点u，存在则返回顶点表中的下标；否则返回-1int i;for(i=1;i<=G.vexnum;i++)if(u == G.vertices[i].data)return i;return -1;
} //创建无向图G 
bool CreateUDG(ALGraph &G){ cout << "请输入总结点数和总边数：" << endl; cin>>G.vexnum>>G.arcnum;//输入总顶点数，总边数cout << " 输入各顶点值： " << endl; for(int i = 1;i <= G.vexnum;i++){//输入各顶点，构造表头结点表 cin>>G.vertices[i].data;//输入顶点值 G.vertices[i].firstarc=NULL;//初始化表头结点的指针域}//forgetchar();//输入各边，构造邻接表cout << "输入一条边依附的两个顶点值"<<endl; for(int k=1;k<=G.arcnum;k++){char v1,v2;cin>>v1>>v2;    //输入一条边依附的两个顶点 getchar();int i=LocateVex(G,v1);int j=LocateVex(G,v2); //确定顶点在G.vertices中的序号ArcNode *p1=new ArcNode;  //生成一个新的边结点*p1p1->adjvex=j;  //邻接点序号为j //头插法将新结点*p1插入顶点vi的边表头部 p1->nextarc=G.vertices[i].firstarc;G.vertices[i].firstarc=p1; ArcNode *p2=new ArcNode;p2->adjvex=i;  //邻接点序号为i//头插法插入p2 ,因为是无向网，所以是两条 p2->nextarc=G.vertices[j].firstarc;G.vertices[j].firstarc=p2; }//forreturn true; 
}//CreateUDGint main()
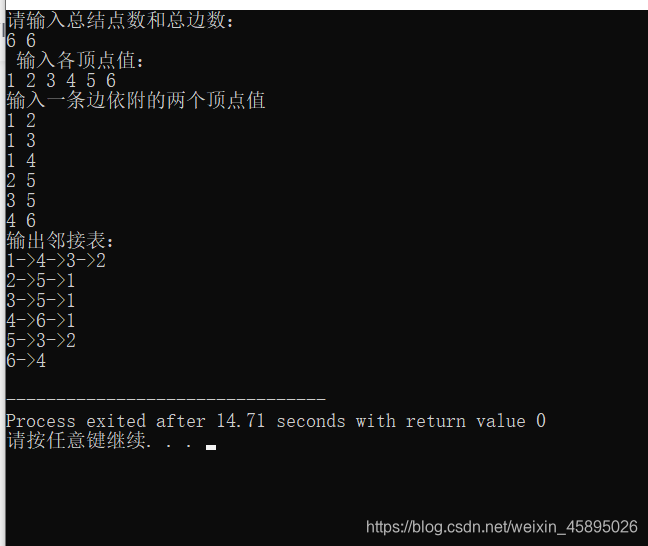
{ALGraph G;ArcNode *p;CreateUDG(G);cout << "输出邻接表： " <<endl;for(int i = 1; i<= G.vexnum; i++){cout << G.vertices[i].data;for(p = G.vertices[i].firstarc; p != NULL; p = p->nextarc)printf("->%d", p->adjvex);cout << endl; } return 0;
}