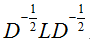参考文档:参考

1.什么是聚类

定义

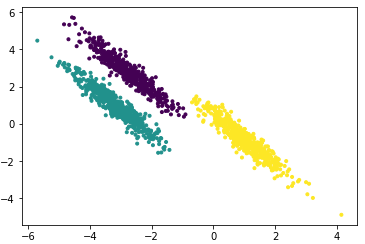
聚类(Clustering) 是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

聚类和分类

1. 聚类(Clustering)：是指把相似的数据划分到一起，具体划分的时候并不关心这一类的标签，目标就是把相似的数据聚合到一起，聚类是一种**无监督学习(Unsupervised Learning)**方法。
2. 分类(Classification)：是把不同的数据划分开，其过程是通过训练数据集获得一个分类器，再通过分类器去预测未知数据，分类是一种监督学习(Supervised Learning)方法。

一般过程

1. 数据准备：特征标准化和降维
2. 特征选择：从最初的特征中选择最有效的特征，并将其存储在向量中
3. 特征提取：通过对选择的特征进行转换形成新的突出特征
4. 聚类：基于某种距离函数进行相似度度量，获取簇
5. 聚类结果评估：分析聚类结果，如距离误差和(SSE)等

数据对象之间相似度度量

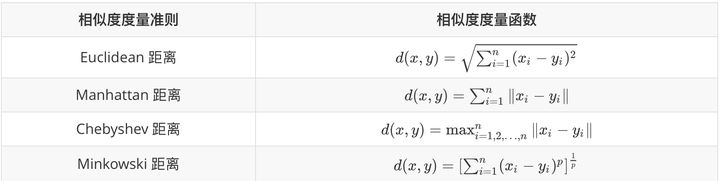
聚类之间的相似度度量

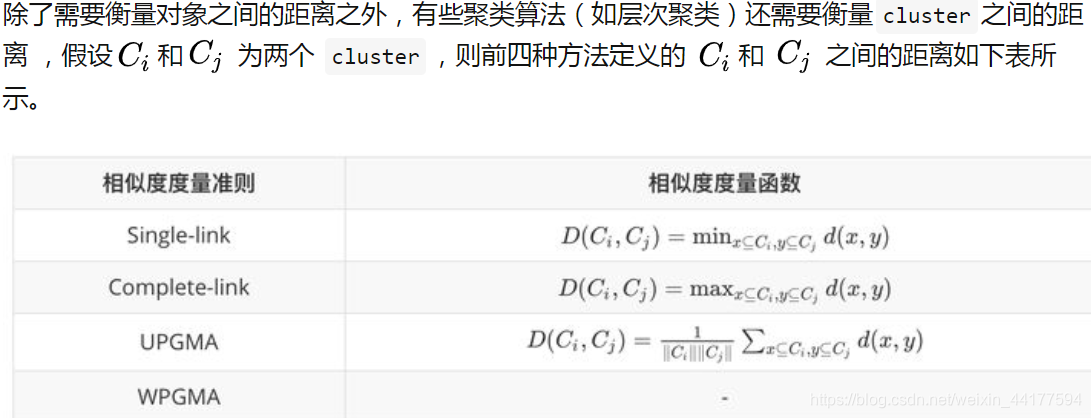
• Single-link定义两个cluster之间的距离为两个cluster之间距离最近的两个点之间的距离，这种方法会在聚类的过程中产生链式效应，即有可能会出现非常大的cluster
• Complete-link定义的是两个cluster之间的距离为两个cluster之间距离最远的两个点之间的距离，这种方法可以避免链式效应,对异常样本点（不符合数据集的整体分布的噪声点）却非常敏感，容易产生不合理的聚类
• UPGMA正好是Single-link和Complete-link方法的折中，他定义两个cluster之间的距离为两个cluster之间所有点距离的平均值
• 最后一种WPGMA方法计算的是两个 cluster 之间两个对象之间的距离的加权平均值，加权的目的是为了使两个 cluster 对距离的计算的影响在同一层次上，而不受 cluster 大小的影响，具体公式和采用的权重方案有关。

2.聚类方法

分类如下

2.1 划分式聚类方法

划分式聚类方法需要事先指定簇类的数目或者聚类中心，通过反复迭代，直至最后达到"簇内的点足够近，簇间的点足够远"的目标。

经典的划分式聚类方法有k-means及其变体k-means++、bi-kmeans、kernel k-means等。

k-means

流程

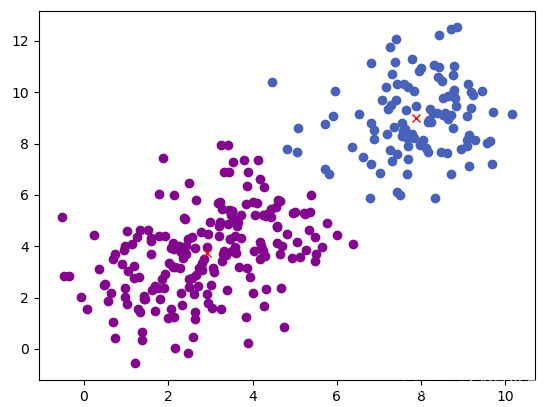
演示：


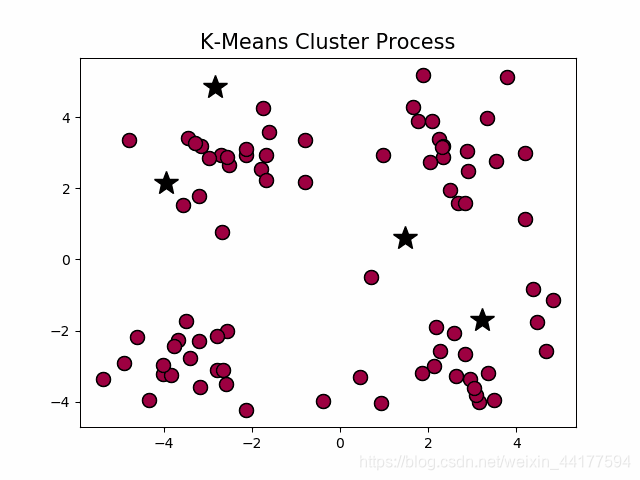
k-means的问题：

1. 需要提前确定k值
2. 对初始质心点敏感
3. 对异常数据敏感

k-means++

k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似，改变的地方只有初始质心的选取，该部分的算法流程如下:

bi-kmeans

一种度量聚类效果的指标是SSE(Sum of Squared Error)，他表示聚类后的簇离该簇的聚类中心的平方和，SSE越小，表示聚类效果越好。

bi-kmeans是针对kmeans算法会陷入局部最优的缺陷进行的改进算法。该算法基于SSE最小化的原理，首先将所有的数据点视为一个簇，然后将该簇一分为二，之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否能最大程度的降低SSE的值。

流程

基于密度的方法

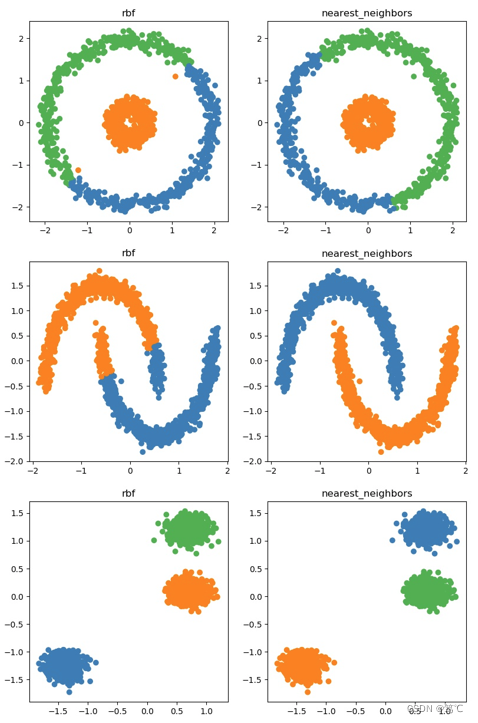
k-means算法对于凸性数据具有良好的效果，能够根据距离来讲数据分为球状类的簇，但对于非凸形状的数据点，就无能为力了，在环形数据的聚类时：

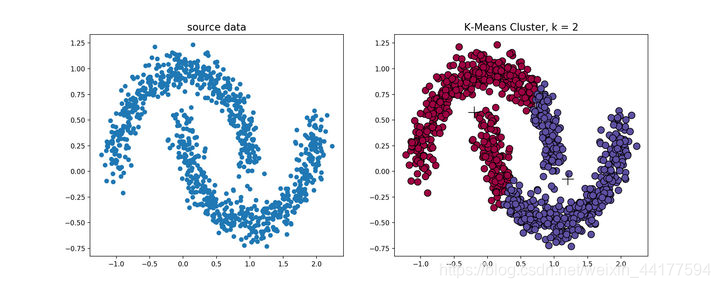
基于密度的聚类方法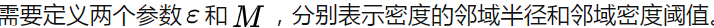

DBSCAN

可以看看这个博客：DBSCAN

特点在于：

1. 需要提前确定密度邻域半径和领域密度阈值
2. 不需要提前设置聚类的个数
3. 对初值选取敏感，对噪声不敏感
4. 对密度不均的数据聚合效果不好

可视化

OPTICS算法

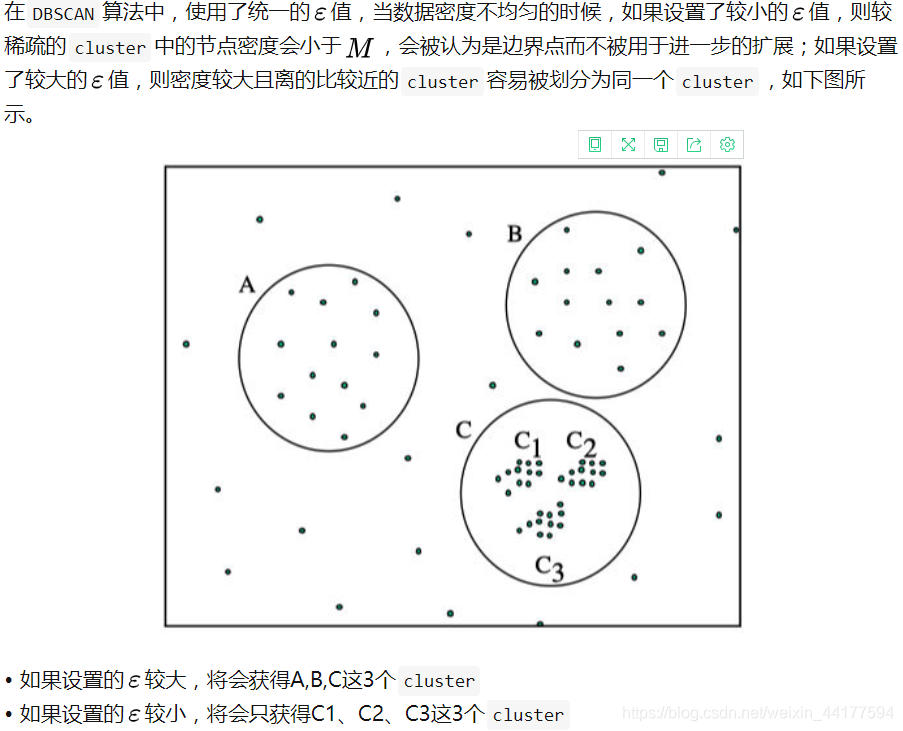
所以问题是如何选择合适的邻域密度值

OPTICS(Ordering Points To Identify the Clustering Structure, OPTICS)实际上是DBSCAN算法的一种有效扩展，主要解决对输入参数敏感的问题。即选取有限个邻域参数[公式] 进行聚类，这样就能得到不同邻域参数下的聚类结果。

可以看看这个

层次化聚类算法

层次聚类算法 (hierarchical clustering) 将数据集划分为一层一层的 clusters，后面一层生成的 clusters 基于前面一层的结果。层次聚类算法一般分为两类：

1. Agglomerative 层次聚类：又称自底向上（bottom-up）的层次聚类，每一个对象最开始都是一个 cluster，每次按一定的准则将最相近的两个 cluster 合并生成一个新的 cluster，如此往复，直至最终所有的对象都属于一个 cluster。这里主要关注此类算法。
2. Divisive 层次聚类： 又称自顶向下（top-down）的层次聚类，最开始所有的对象均属于一个 cluster，每次按一定的准则将某个 cluster 划分为多个 cluster，如此往复，直至每个对象均是一个 cluster。

层次聚类是一种贪心算法

核聚类

主要思想：通过一个非线性映射，将输入空间中的数据点映射到高维特征空间中，并选取合适的Mercer核函数代替非线性映射的内积，在特征空间中进行聚类

优点：

1. 普适的
2. 通过非线性映射增加了数据点线性可分的概率，即能较好地分辨、提取并放大有用的特征，从而实现更为准确的聚类，算法收敛速度也较快。

支持向量聚类

支持向量聚类（Support Vector Clustering, SVC）属于核聚类的一种，它以支持向量机（Support Vector Machine, SVM）为工具进行聚类。

基本思想：利用高斯核，将数据空间中的数据点映射到一个高维的特征空间中。再在特征空间中寻找一个能包围所有数据点象的半径最小的球，将这个球映回到数据空间，则得到了包含所有数据点的等值线集。这些等值线就是簇的边界。每一条闭合等值线包围的点属于同一个簇

两个阶段：

1. SVC训练阶段
   SVC训练阶段包括高斯核宽度系数的确定、核矩阵的计算、Lagrange乘子的计算、支持向量的选取和高维特征空间中特征球半径的计算
2. 聚类分配阶段
   聚类分配阶段首先生成邻接矩阵，然后根据邻接矩阵进行聚类分配

优势：

1. 能产生任意形状的簇边界；
2. 能分析噪声数据点且能分离相互交叠的簇。这是许多聚类算法无法做到的

谱聚类

参考

引言

谱聚类想法的起源：如何在给定长度的线条下围出一个最大的面积，也可理解为，在给定面积下如何使用更短的线条。如何在给定一张图，拿出**“更短”**的边来将其“更好”地切分。

• “更短”的边，正是对应了spectral clustering中的极小化问题，
• “更好”地切分，则是对应了spectral clustering中的簇聚类效果

优缺点

优点：

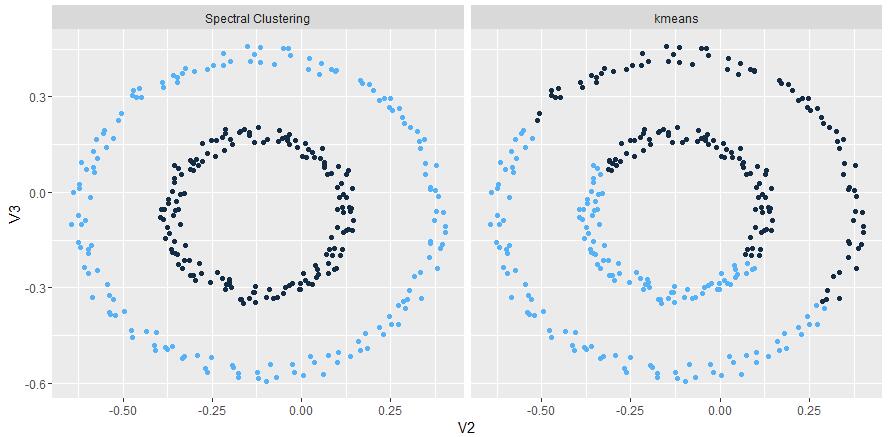
1. 过程对数据结构并没有太多的假设要求，如kmeans则要求数据为凸集。
2. 可以通过构造稀疏similarity graph，使得对于更大的数据集表现出明显优于其他算法的计算速度。
3. 由于spectral clustering是对图切割处理，不会存在像kmesns聚类时将离散的小簇聚合在一起的情况。
4. 无需像GMM一样对数据的概率分布做假设。

缺点：

1. 对于选择不同的similarity graph比较敏感（如 epsilon-neighborhood， k-nearest neighborhood，fully connected等）。
2. 对于参数的选择也比较敏感（如 epsilon-neighborhood的epsilon，k-nearest neighborhood的k，fully connected的 ）。

步骤

第一步是构图，将采样点数据构造成一张网图，表示为G(V,E)，V表示图中的点，E表示点与点之间的边，如下图：

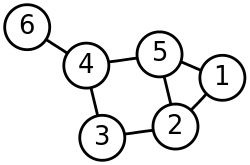
第二步是切图，即将第一步构造出来的按照一定的切边准则，切分成不同的图，而不同的子图，即我们对应的聚类结果，举例如下：

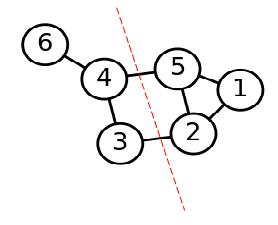
构图的三种方式：

1. ε-neighborhood
2. k-nearest neighborhood
3. fully connected